某机组异常压力脉动下尾水管的处理及其刚强度、疲劳寿命评估

李国慧，严锦丽

(浙江富春江水电设备有限公司,杭州 310013)

0 前 言

某机组在72 h试运行阶段，出现了在50%和60%负荷工况下上机架和顶盖的轴向振幅超出国标[1]要求的报警。经过系统地分析和电站实测，发现是由转轮中心下游出现的异常压力脉动引起的，这种压力脉动主要出现在部分负荷工况。由于机组不可能全部在最优工况下运行，本文为了消除异常压力脉动，选择在尾水管上增加T管的方式，从T管向转轮中心补气，T管补气方案示意见图1。转轮下游通常产生部分负荷涡带，这种方案的原理是影响转轮下游的流体流动，打散涡带，消除压力脉动。

经过现场试验验证，T管补气方案成功地消除了转轮下方的异常压力脉动，机组安全稳定并网。

本文选用大型通用有限元软件ANSYS Workbench[2-7]对某机组的水力性能进行了计算，计算结果亦证明了增加T管的方案成功地消除了涡带。随后进一步对尾水管T管的刚强度和疲劳寿命进行了计算，确保T管能够满足机组长期安全稳定运行的需求。

1 水力计算

1.1 有限体积法的基本思想

有限体积法是从流体运动积分形式的守恒方程出发来建立离散方程，三维对流扩散方程的守恒型微分方程如下：

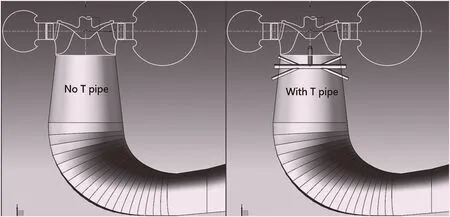
图1 尾水管上有无T管示意图

(1)

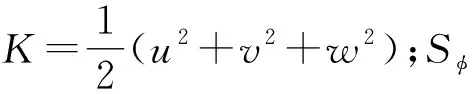
若式(1)用散度和梯度表示：

(2)

将式(1)在时间步长Δt内对控制体体积CV积分，可得：

(3)

式中:散度积分已用格林公式简化为面积积分，A为控制体的表面积。

该方程的物理意义是：Δt时间段控制体CV内ρφ的变化，加上Δt时间段通过控制体表面的对流量ρuφ，等于Δt时间段通过控制体表面的扩张量，加上Δt时间段控制体CV内源项的变化。

ANSYS CFX采用了基于有限元的有限体积法[8]，在保证了有限体积法守恒特性的基础上，吸收了有限元法的数值精确性。例如，基于有限元的有限体积法，对六面体网格单元采用24点积分，对四面体网格单元采用60点积分；而单纯的有限体积法，对六面体网格单元采用6点积分，对四面体网格单元采用4点积分。

三维计算流体力学(CFD)模型计算时，根据流体与时间的关系，一般流动可以分为稳态流动和非稳态流动(瞬态流动)。稳态流动是指流体的流动与时间变量无关，计算域内任意一点的物理量不随时间的变化而变化。从数学角度上讲，就是物理量对时间的偏导数为零。而非稳态流动是指流体的流动随时间的变化而变化，物理量是时间的函数。

1.2 稳态计算结果

CFD计算模型见图2，模型包含了蜗壳、固定导叶、活动导叶、转轮、尾水管及T管，选取高质量网格进行划分，网格数量约800万个。

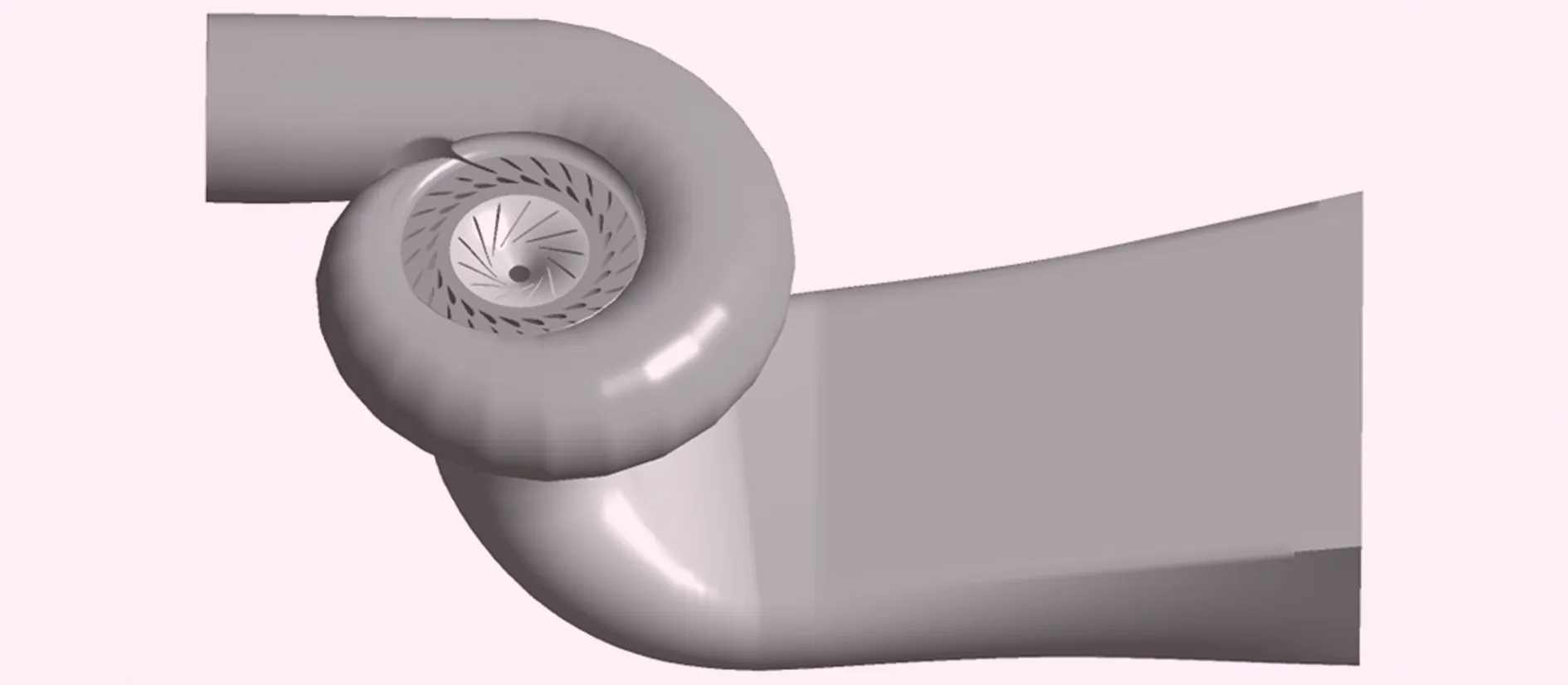
图2 CFD计算模型图

以50%负荷工况为例，有、无T管时尾水管压力分布见图3，可见尾水管内增加T管后，肘管内的低压区消失，压力分布变得均匀。在此部分负荷工况下，尾水管内有空腔涡带产生，增加T管后，尾水管内涡带被打散。

1.3 非稳态计算结果

增加T管后对机组进行CFD瞬态分析，同样以50%负荷工况为例，不同时刻尾水管内的压力分布见图4。可见在1个旋转周期R内，尾水管内的压力分布趋势变化比较明显。后续会对T管进行动应力计算，在尾水管过流面上施加此随时间变化的水压力，得到随时间变化的应力曲线，进而进行疲劳寿命评估。

其次，构建完整的植物群落结构研究体系。针对不同区域、不同场地的城乡环境，将研究视角放在“点”“线”“面”的逐级深化研究，深入研究民居单体与聚落群体之间、植物特性与植被群体组合之间的植物搭配文化，完善本地民居的植物群落结构的搭配文化。

图3 50%负荷工况下，有、无T管时尾水管压力分布图

2 尾水管静强度计算

增加T管后，对尾水管进行静强度校核，流道内的水压力分布来自1.2小节CFD稳态计算结果。

计算50%负荷工况时(T管应力分布见图5)，最大应力23.6 MPa，出现在B区;60%负荷工况时，最大应力27.0 MPa，亦出现在B区;100%负荷工况时，最大应力8.5 MPa，出现在A区。计算结果汇总见表1。

结论：尾水管材料为Q235B，其屈服强度为235 MPa。T管材料为不锈钢S304，其屈服强度为205 MPa。根据表1计算结果，尾水管及T管静强度满足设计要求。

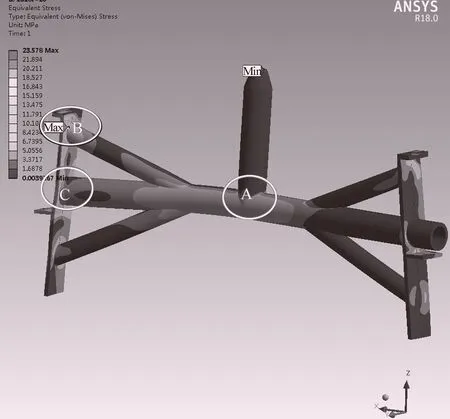
图5 T管应力分布图

3 尾水管动应力计算及疲劳评估

根据第2节计算结果，增加T管后，得到了A、B、C(见图5)3个待关注的危险区域。首先，采用瞬态计算法，在尾水管的过流面上施加随时间变化的压力场(压力场来自1.3小节计算结果)，计算得到整个尾水管的应力分布；其次通过后处理提取A、B、C区域的应力分布曲线；最后，对尾水管T管进行疲劳评估，以确保其疲劳寿命满足要求。

50%负荷工况时，经过瞬态计算，得到了A、B、C关注区域的应力分布，见图6。类似的，不同负荷工况下，A、B、C关注区域的应力分布见图7、8。

各个关注位置的平均应力及应力幅值汇总见表2。

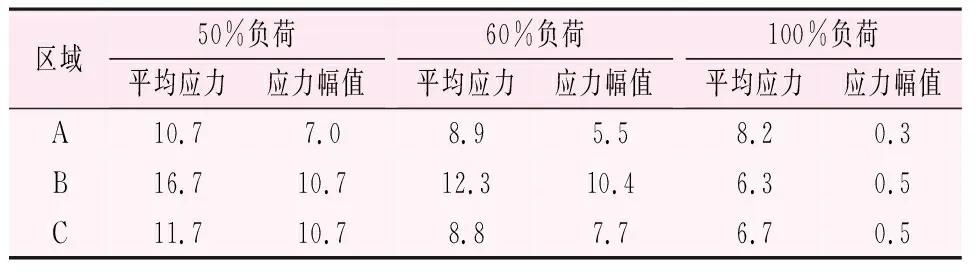
表2 平均应力和应力幅值结果汇总表 /MPa

现用Goodman疲劳极限线图[9]进行疲劳评估，Goodman图线假设疲劳极限线是经过对称循环疲劳极限点和静强度极限点的一条直线，其表达式方程为：

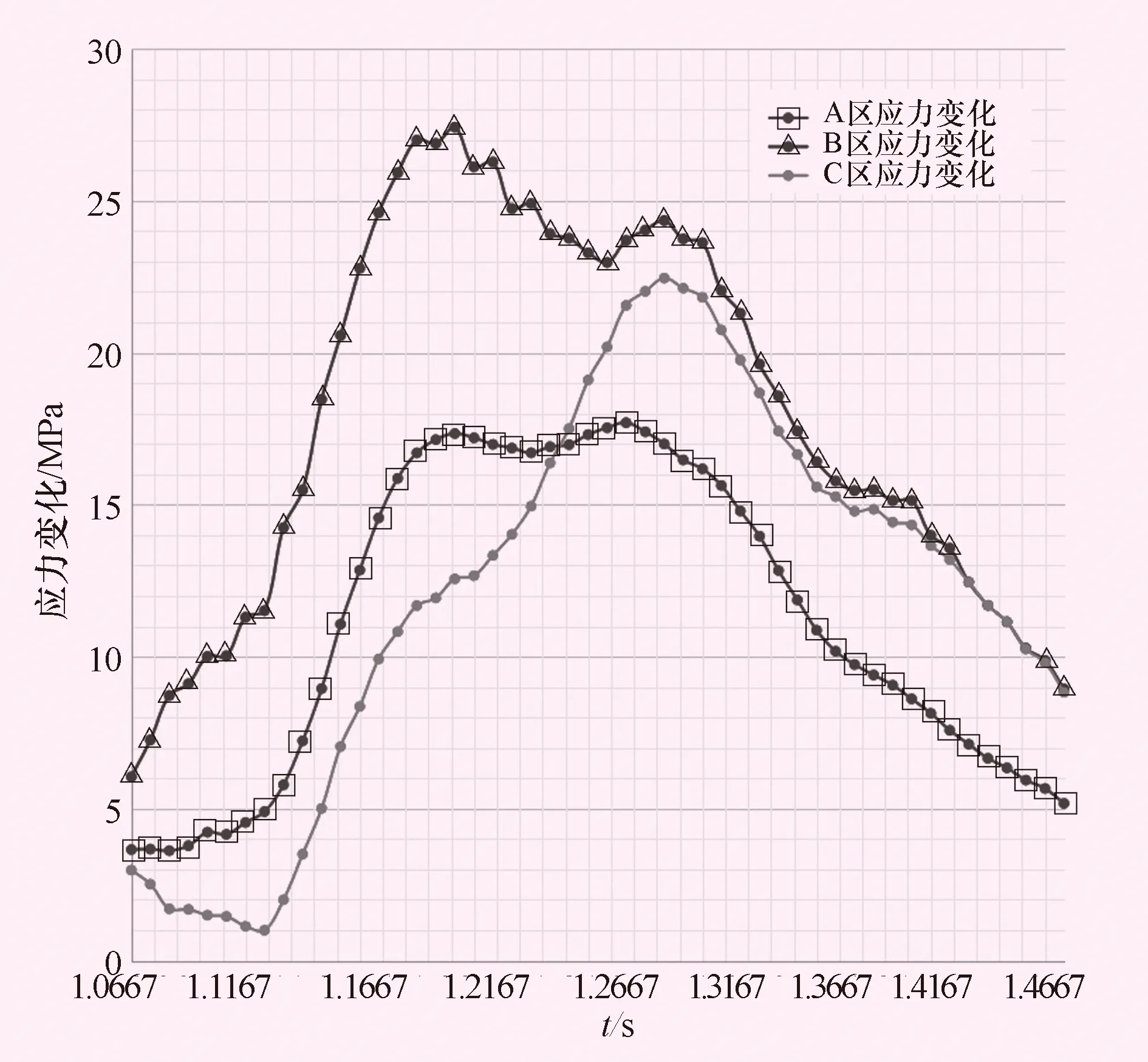
图6 50%负荷工况时，A、B、C关注区域的应力分布图

图7 60%负荷工况时，A、B、C关注区域的应力分布图

图8 100%负荷工况时，A、B、C关注区域的应力分布图

(4)

式中：σb为材料的强度极限；σa为平均应力；σm为应力幅值；σ-1为材料的对称循环疲劳极限。

上述Goodman图线是针对材料进行评价，使用时需要考虑修正系数，变换到具体的结构上。即，需要考虑尺寸系数、腐蚀系数、缺口系数对结构的影响，进而求出结构(此处为T管)的疲劳极限。

结构的疲劳极限计算公式为：

σw=σw0ξ1ξ2/β

(5)

式中：σw0为材料疲劳极限；ξ1为尺寸系数；ξ2为腐蚀系数；β为缺口系数。

T管材料为不锈钢S304，屈服强度σs=205 MPa，抗拉强度σb=500 MPa。T管材料的疲劳极限σw0=98 MPa。尺寸系数取值ξ1=0.55。腐蚀系数ξ2=1；缺口系数β=1。

根据相关试验结果，需考虑疲劳安全率取值f=1.5。则，结构的疲劳极限σw=98×0.55/1.5=35 MPa。

根据有关文献[10]，应力波形对疲劳强度的影响较小，所以在一般的疲劳强度设计中，不考虑应力波形对疲劳寿命的影响。

由此作出修正的Goodman曲线如图9。A、B、C评估点均位于Goodman曲线左下方，表示结构设计合理，T管不会发生疲劳失效。

图9 Goodman曲线图

腐蚀及应力集中同时作用的疲劳极限见表3，则材料的疲劳极限取为98 MPa。

结论：根据Goodman线图，A、B、C区域评估点均位于Goodman曲线左下方，表示结构疲劳强度设计合理，T管不会发生疲劳失效。

4 结 论

(1) 在尾水管内增加T管补气后，成功地消除了转轮下方的异常压力脉动，使机组能够安全稳定并网。

(2) 对机组进行稳态CFD分析，计算得到的水压力分布施加在尾水管流道面上。采用有限元法对尾水管进行静强度计算，计算结果表明尾水管刚强度满足要求。

(3) 对机组进行非稳态CFD分析，计算得到的水压力分布施加在尾水管流道面上。采用有限元法对尾水管进行动应力计算并对危险区域进行疲劳评估，计算结果表明尾水管及T管疲劳强度满足要求。

5 说 明

(1) 本次刚强度及动应力计算结果，是基于尾水管和T管完全焊透的情况下得到的。如果焊缝质量和本报告的计算模型达不到等强度要求，则无法保证实际T管的刚强度和疲劳寿命。所以，实际操作过程中，设计师应对焊缝质量提出相应的要求。

表3 腐蚀环境及应力集中同时作用的疲劳极限表

(2) 根据本文计算结果，尾水管在部分负荷工况下的应力波动相对最优工况差。鉴于上下游水位及自然丰枯年对河流水量的影响，设计时T管亦满足其在部分负荷工况下安全运行的要求。