色彩感知中的脑电信号多域特征选择算法研究

李 庆 薄 华

(上海海事大学信息工程学院，上海 201306)

1 引言

当人眼感知不同的色彩时，其脑电信号(Electroencephalography， EEG)在波形、幅度等特性上存在着一定的差异。早期在通过脑电信号对色彩感知的研究中，主要是采用目测脑电图来寻找不同脑电信号之间的差异。然而随着电子计算机技术的飞速发展，脑电信号分析进入了计算机分析的时代，通过计算机分析不同的脑活动所反应出的不同脑电特性，来对色彩感知加以分类识别。Muhammad Masud Rana[1]等将时域统计特性和频域特性有效的结合，提取时域统计特性的均值、最大值和频域特性的功率谱密度，对绿色、蓝色、红色和黄色四种颜色进行识别分类，识别正确率较单个域的特性有所提高。Suchada Tantisatirapong[2]等采用幅度平方相干分析(Magnitude-squared Coherence, MSC)算法来研究脑电信号的稳态视觉诱发信号，发现红色和绿色分别在theta和alpha频带上有最大的MSC系数，以此系数作为特征向量来对这两种颜色进行分类，结果表明MSC系数能够有效的将红色和绿色区分。

EEG信号是非平稳、非线性的随机信号[3]，小波能量能够反应EEG信号在各个频率的能量情况。Bony Thomas[4]等采用小波变换(Wavelet Transform, WT)的方法，提取脑电信号的小波能量和熵进行色彩观测识别，取得了较好的识别正确率。刘冲[5]等利用小波变换提取脑电信号各频段的能量作为特征向量，使用K-近邻法进行脑电信号分类，最大正确率达到85.7%。

研究表明，在分析脑电信号上采用小波变换技术，利用小波变换发掘各小波的特性作为分类器的输入，能够有效的将脑电数据分类。但就如何充分的挖掘脑电信号的时域特性，并将其与小波能量融合，有效的将基于不同色彩感知中的脑电信号分类，目前相关的研究还不多见。本文将采用16导脑电数据，对感知红、绿、蓝三种颜色的脑电进行分析，结合时域统计特性偏度(Skewness)、峰度(Kurtosis)与小波能量作为特征向量，采用基于随机森林(Random Forests, RF)的特征提取算法，筛选出最佳的特征组合方式，实现基于色彩感知中的脑电信号识别。

2 实验数据来源

实验所用的数据采集设备为16导的Neuroscan脑电放大器，采样频率为1000 Hz，16个电极在头皮的分布如图1所示。本文所用作分析的数据已经进行了一些预处理，比如去除眼电(EOG)和滤除大于50 Hz的工频干扰[6]，并将最终的脑电信号存储为matlab能够识别的格式。

实验志愿者为4名年龄在22到25岁的研究生，2男2女，要求每个志愿者身心健康、无任何精神类疾病病史。采集环境处于安静的实验场所；志愿者在采集数据前要求将头皮洗净，采集过程中保持头脑清醒。采集前用酒精对脑电采集仪的电极进行清洁。

图1 电极位置示意图Fig.1 Position of electrodes

采集过程中，首先让志愿者处于闭眼静心的状态下测一组10 s数据作为参考组，然后通过屏幕对红、绿、蓝三种颜色进行播放，每种颜色停留30 s，三种颜色之间穿插10 s黑屏状态，三种颜色每循环一次有120 s的过渡时间让志愿者放松平静，并让志愿者写下每次测试的状态评估表。按照上述采集步骤，分别采集4个志愿者的脑电信号，以1 s长度的信号为一组样本，最终采集到有效样本591组，红色样本196组，绿色样本196组，蓝色样本199组。

3 脑电信号的特征提取与选择方法

3.1 时域统计特征

时域统计分析通常作为处理大量数据的一种方法，能够客观地描述一组数据与历史数据间的关联。脑电信号作为一种典型的非线性、非高斯的随机信号，一般的时域统计特征：最大值、最小值、均值、协方差等并不能很好描述脑电信号的这些特性，而偏度、散度作为衡量信号的不对称性与陡峭性的统计量(二则均是与正态分布进行比较)，能够很好的描述脑电信号的非线性与非高斯性这些特性，因此本文将采用偏度、峰度作为脑电信号的时域统计特征。

偏度是描述数据集概率分布不对称性的一种度量，其不对称性的衡量是与正态分布进行比较。公式(1)用于计算数据集的偏度。当偏度为0时，表示数据集的分布与正态分布的偏斜度相同；偏度大于0时，表示数据集的分布与正态分布相比是正偏或右偏；偏度小于0时，表示数据集的分布与正态分布相比是负偏或左偏[7]。偏度的绝对值越大表示偏斜度越大。

(1)

峰度是用于描述数据分布的陡缓程度，其陡缓程度的衡量也是与正态分布进行比较。可以用公式(2)来计算数据集的峰度。当峰度为0时，表示数据集的分布与正态分布的陡缓程度相同；峰度大于0时，表示数据集的分布与正态分布相比更为陡峭，称其为尖顶峰；峰度小于0时，表示数据集的分布与正态分布相比更为平缓，称其为平顶峰[7]。峰度的绝对值越大表示数据集分布形态的陡缓程度与正态分布的差异越大。

(2)

图2给出了591组脑电信号样本每一导数据上的平均偏度值分布情况。可知，在C4导联上感知三种不同颜色的脑电信号在偏度值上有明显的区别，且在感知绿色时脑电信号的偏度最大，感知红色时脑电信号的偏度最小。图3为峰度值的平均分布情况，该特征出现与偏度值类似的现象，同样是在C4导联上有明显的区别，但在该导联上，峰度值最大的为感知蓝色的脑电信号，最小的仍然为感知红色的脑电信号。

图2 16导脑电信号的偏度统计量Fig.2 The statistical measures of skewness for sixteen channels’EEG signals

图3 16导脑电信号的峰度统计量Fig.3 The statistical measures of kurtosis for sixteen channels’EEG signals

3.2 小波能量

人的眼睛在看某种颜色时，大脑对应的视觉联络区的脑电δ节律(1～4 Hz)、 θ节律(4～7 Hz)、α节律(8～13 Hz)、 β节律(14～30 Hz)会出现相应的变化[8]。根据这一特征，可以提取脑电信号这四个节律的能量值来分析感知到不同色彩的脑电信号的区别。而小波变换具有多分辨率特性，可以按实际要求调整时间窗和频率窗，来获取不同频带的信号分量[9]，因此可以使用小波变换对脑电信号进行分析。

连续小波变换(Continuous Wavelet Transform, CWT)定义为：

(3)

不同于傅里叶变换，小波变换有两个变量：尺度变量a(scale)和平移变量τ(translation),尺度变量和平移变量分别能够调节小波基函数的伸缩和平移[10]。

而在实际应用中，为了便于计算机的处理，需要将连续小波进行离散化。设实验采集的离散脑电信号为x(n)，离散小波变换可以用公式(4)表示：

,j,k∈Z

(4)

其中，ψ(n)为小波基函数，j,k分别为小波的频域分辨率和时域平移量。采用Mallat算法对信号进行分解，用公式表示为：

(5)

L为信号的分解层数，AL为第L次分解后低频逼近系数，Dj为不同尺度变换下的细节系数。

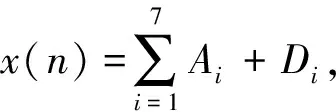
(6)

图4～7是所采集到的591组16导脑电信号的小波能量均值的分布情况。由此可知，delta节律上的能量在Fp1和F3导联上有明显的区别，thelta节律上的能量在P4和O1导联上有明显的区别，alpha节律上的能量在O2导联上有明显区别，beta节律上的能量则在Fp1导联上有明显区别。

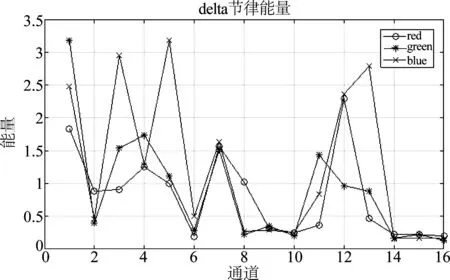
图4 16导脑电信号的delta节律能量Fig.4 Delta band energy for sixteen channels’EEG signals

图5 16导脑电信号的thelta节律能量Fig.5 Thelta band energy for sixteen channels’EEG signals

图6 16导脑电信号的alpha节律能量Fig.6 Alpha band energy for sixteen channels’EEG signals

图7 16导脑电信号的beta节律能量Fig.7 Beta band energy for sixteen channels’EEG signals

3.3 随机森林的特征选择算法

通过上述的时域统计特征提取方法，可以提取到2×16=32维的特征；频域特征提取方法，可以提取4×16=64维特征，特征维数总和为96维，而由图1～6可知并不是所有的特征都对分类有帮助，特征之间往往存在冗余的特征和异常的特征，这些特征通常都会降低分类器的识别率，基于此本文提出采用基于随机森林(Random Forest，RF)算法的特征选择方法。该方法是以特征向量子集的熵值为依据，评价每个特征对最终分类效果的贡献度，从而选出最优的特征向量子集。在研究过程中将使用CART决策树来构建随机森林，即使用Gini系数来划分特征。Gini系数反映的是数据集的不纯度，Gini系数越小，则数据集的不纯度越低，选取的特征对数据的分类效果越好[11]。原始数据集D的Gini系数计算如公式(7)所示：

(7)

其中k(k=1，2…，|y|)为数据类别，pk表示数据集D中第k类样本所占的比例。

而对于给定的脑电信号样本集D，假设有K个类别，第k个类的样本个数为Ck，则样本D的Gini系数表达式如(8)所示：

(8)

假设样本集D中的特征A能够把样本分成D1和D2两部分，则在基于特征A的条件下，样本集D的Gini系数的表达式可以进一步表示为：

(9)

随机森林的每一棵决策树，都是对特征向量进行采样，然后计算当前的Gini系数，每一棵树的非叶子节点都有一个Gini系数，通过Gini系数作为特征重要性排序的依据，每当一颗决策树生长完成后都可以得到各个节点的重要性排序。建立多棵决策树构成森林，生成多个特征重要性排名，通过“投票”机制选取前m个特征构成特征向量集。

4 AdaBoost分类算法

实验所采集的脑电数据包含了大脑感知不同色彩状态下连续变化的脑电信息[12]，且这些数据属于数值型数据，因此可以采用自适应增强算法(Adaptive Boosting, AdaBoost)来对脑电信号进行分类。AdaBoost算法属于一种提升(boosting)学习算法[13]，其提供的是一种算法框架，可以使用在机器学习中所了解的各种弱分类算法来构建子分类器，通过将多个弱分类器进行加权融合形成一个具有很高精度的分类器，该算法同时具有结构简单、易于理解，泛化能力强等优点，因此本文采用该算法对脑电信号进行分类。AdaBoost算法的具体流程如下：

步骤1 初始化训练数据的权值D1。每个训练样本的初始权值为1/N。

D1=(ω11,ω12,…,ω1i,…,ω1N),

(10)

步骤2 使用具有权值的训练样本Dm进行学习，产生弱分类器，并计算该弱分类器分类误差率。

a)弱分类器：Gm(x):χ→{-1,+1};

(Gm(xi)≠yi)。

步骤3 更新训练样本的权值。提高错分样本的权值，降低正确分类样本的权值，将更新后的训练集执行步骤2。

Dm+1=(ωm+1,1,…,ωm+1,i,…,ωm+1,N)

(11)

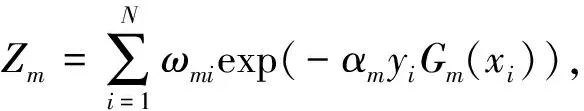
步骤4n次迭代更新，产生n个弱分类器，计算各个弱分类器的权重。

(12)

步骤5 对这n个弱分类器进行加权融合，产生最后的结果分类器。

(13)

本文将采用logistic回归算法构造弱分类器，并对训练样本的权值进行50次迭代更新。

5 结果与分析

在训练分类器时采用10折交叉验证，即将样本数据集随机分成10等份，每次拿出9份作为训练样本，1份用作测试样本。图8为使用随机森林特征选择算法提取出不同维数的特征向量子集对脑电信号的识别率分布图，可知最优的特征向量子集的维数为6维。

图8 不同维数的特征向量子集的识别率Fig.8 The recognition rate of feature vector subsets with different dimensions

表1为不同特征向量集下对不同色彩感知的脑电信号识别的平均正确率。

表1 不同特征向量集下分类的平均正确率

在表1中，单独采用时域统计量偏度和峰度作为特征向量来识别不同色彩感知中的脑电信号时，使用AdaBoost分类器平均分类正确率可达到55.3%。单独采用小波能量作为特征向量时，平均分类正确率达到67.5%。可以发现小波能量作为特征要比偏度、峰度作为特征识别率上要提高10%左右，这是由于小波能量所蕴含的脑电信号的信息量上要比偏度和峰度要多。当二者进行结合时，平均分类正确率达到75.2%，分类效果要优于使用单一类型的特征量。而采用本文所提出的随机森林特征选择算法，提取最优的特征组合：C4导的偏度和峰度、FP1导delta节律能量、P4导thelta节律能量、O2导alpha节律能量和Fp1导beta节律能量，识别率提高10%左右，这说明该方法能够提取出不同色彩感知的脑电信号间的最大差异性信息，从而达到提升分类效果作用。

本文的实验方法与其他文献的方法进行比较，如表2所示。实验比较过程中，实验的数据均为所采集到的591组脑电数据，实验所用到的分类器均为使用logistic回归算法经过50次迭代更新得到的AdaBoost分类器。

表2 不同文献所使用的特征分类结果对比

表2中，采用文献[1-2,14-16]所使用的特征进行分类，分类效果最好的为文献[16]所使用的小波熵和自回归模型搭配的特征组合方案，平均分类正确率可达到78.8%；分类效果最差的为文献[14]所使用的方案，该方案使用自回归模型作为特征，平均分类正确率仅仅达到70.8%；而使用本文的方法来进行分类，平均分类正确率皆高于其他文献，可以更好的识别感知不同色彩的脑电信号。

6 结论

本文针对基于色彩感知中的脑电信号分类的问题，提出将偏度、峰度统计量与小波能量特征进行结合，采用基于随机森林算法的特征选择方法提取最优的特征向量子集，输入到AdaBoost分类器中进行学习，并与单一类型的特征量进行比较。结果表明：1)偏度、峰度统计量与小波能量组成的特征向量能够有效的将色彩感知中的脑电信号进行分类，平均分类正确率达到85.07%，识别效果要优于单一类型的特征量；2)本文提出采用基于随机森林特征选择算法提取最优的特征向量子集，达到提升分类器分类效果，通过实验对比证明该算法是有效的；3)本文虽以三种色彩感知为研究对象，但其使用的特征提取与选择算法仍适用于四种或者更多种色彩感知的研究中，所以下一步的工作将围绕更多种色彩感知中的脑电信号识别进行展开。从脑-机接口的实时性来说，在采用本文所提出的特征选择算法提取最优的特征向量子集的同时，应尽可能在保证分类的正确率方面通过空间变换将特征向量子集映射到低维空间中进一步降低特征向量集的维度，缩短分类模型的训练时间，因此后期也将围绕这方面的工作进行研究，以便能够实现对色彩感知中的脑电信号的在线识别，这也是作者对后期研究工作的展望。