赵固二矿回采巷道非对称变形数值模拟分析

郭林峰

(中国矿业大学(北京)资源与安全工程学院，北京市海淀区，100083)

随着开采深度的增加，深部回采巷道围岩变形问题愈加严重。近年来，一些学者针对深部巷道围岩变形机理和控制技术做了大量研究，取得丰厚的研究成果。王虎胜等对不同煤柱宽度下沿空掘巷围岩应力分布特征进行了分析。黄万朋从巷道围岩本身的性质出发分析巷道非对称变形，认为巷道断面内围岩结构的非对称性导致巷道非对称变形。以往学者对于巷道非对称变形主要从巷道围岩本身性质和巷道围岩应力分布的角度分析，然而针对区域主应力场偏转导致的巷道非对称变形鲜有研究。本文针对赵固二矿11071工作面运输巷非对称变形的问题，采用理论分析与数值模拟结合的方法，推导出研究区域主应力场偏转的数值模拟边界加载条件表达式，并以此为前提对该巷道围岩区域主应力场偏转不同角度时的塑性区形态特征进行了分析。

1 工程概况

赵固二矿位于焦作煤田东部、矿井产量180万t/a，主采煤层为二1煤层，厚度6.0～6.59 m，平均6.32 m，煤层结构简单，煤质变化很小，煤类单一，层位稳定。11071工作面采用分层开采，顶板采用全部垮落法管理。该工作面东北侧为未开采的实体煤，西南侧为已回采结束的11050工作面，11071工作面运输巷与11050工作面采空区间隔30 m煤柱，该巷道埋深约700 m，沿煤层顶板掘进，巷道断面形状为矩形，尺寸为4800 mm×3300 mm(宽×高)，巷道净断面15.84 m2。巷道布置平面图如图1所示。

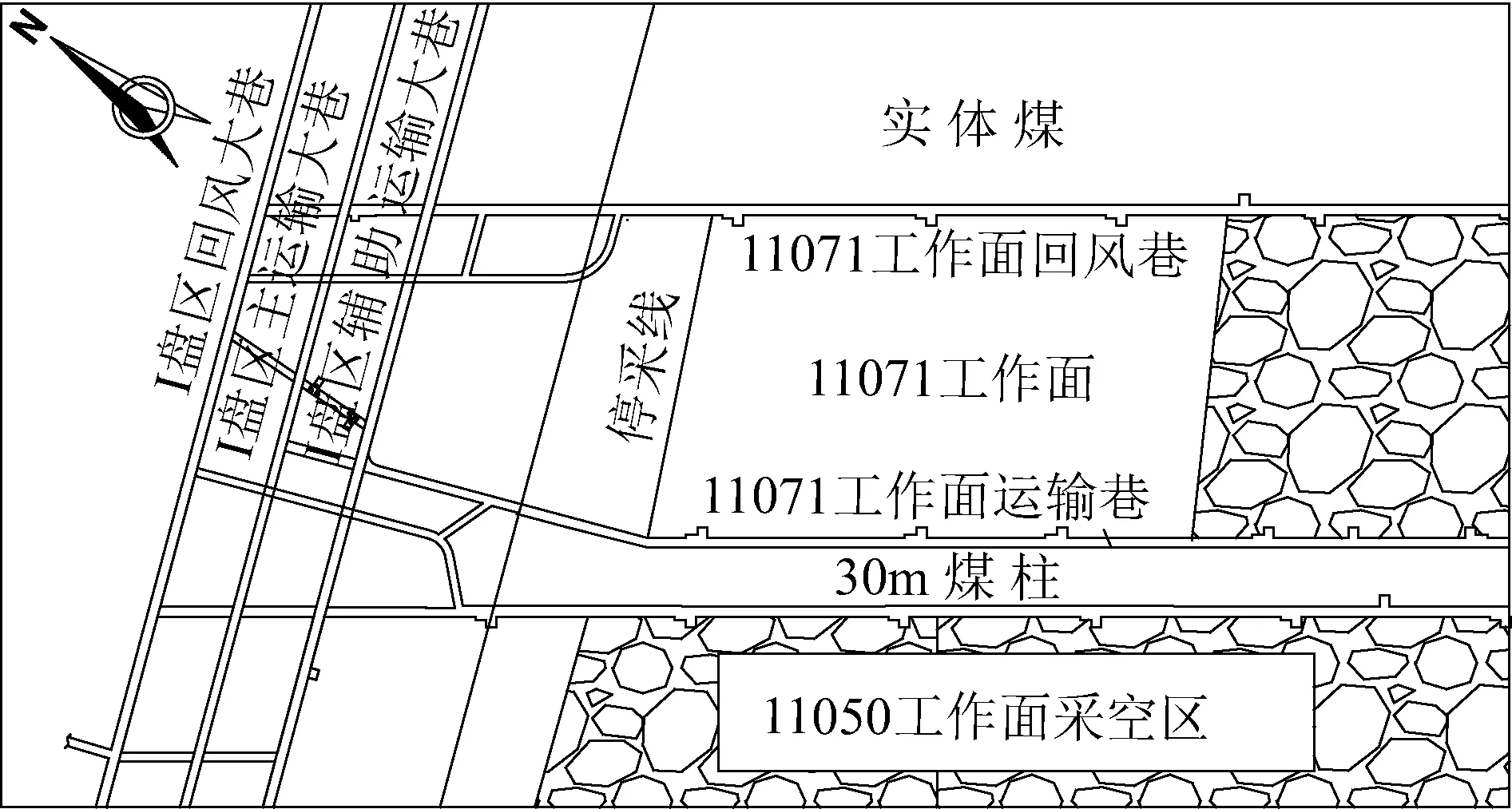
图1 11071工作面运输巷布置平面图

2 11071工作面运输巷围岩非对称变形特征

由于巷道埋深较大，并且紧邻11050工作面采空区，在工作面回采期间，11071工作面运输巷矿压显现剧烈，具有以下特征：顶板下沉量较大，尤其巷道靠近煤柱侧顶板下沉严重；底臌现象突出，尤其巷道靠近煤壁侧底板底臌量较大；两帮发生收敛，两帮收敛量与顶底板移近量接近，巷道整体断面收缩量较大；大量锚索破断，支护体失效。

为满足运输和通风要求，11071工作面运输巷已进行多次返修作业，累计扩帮约2.5 m，卧底约1.7 m，以确保工作面正常生产。巷道变形轮廓图如图2所示。

由于回采巷道直接为采煤工作面服务，距离开采扰动源较近，是受采动影响最剧烈的一类巷道。煤层的开采引起围岩应力重新分布，巷道原来的应力状态也发生改变。工作面向前推进过程中，直接顶冒落形成垮落带，基本顶破断后回转下沉使得上覆岩层压力和自重向深部岩体转移，巷道靠近采空区侧围岩受到上覆岩层传递的倾斜方向的力，导致回采巷道区域主应力场方向发生偏转。

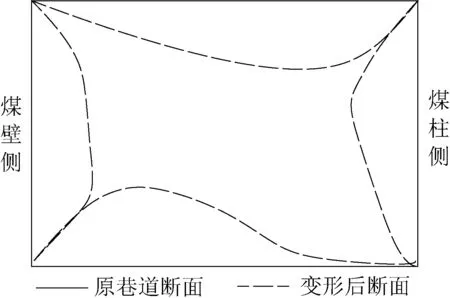
图2 巷道变形轮廓图

3 数值模拟边界加载条件分析

采用数值模拟方法对巷道围岩进行稳定性分析时，通常在巷道周边一定范围内建立有限元模型，以往学者在对模型加载时一般不考虑区域主应力场发生偏转，其受力状态如图3(a)所示。X面只受到水平应力作用为主平面，水平应力为最小主应力；Y方向为巷道轴向，一般认为水平面两个方向的应力相等；模型Z面只受到垂直应力作用为主平面，垂直应力为最大主应力，考虑采动影响后，垂直应力大小等于支承压力。具体加载表达式为：

(1)

式中：SXX、SYY、SZZ——分别为X面、Y面、Z面的正应力；

P1、P3——分别为模型最大、最小主应力；

K——支承压力系数，一般取2～4；

γ——岩石容重，取2.5 kN/m3；

H——巷道埋深，m；

λ——侧压系数。

在实际条件下，巷道围岩由于受到采动应力或者断层和褶曲等地质构造的影响，加上地下应力环境的复杂和不确定性，使其区域主应力场发生偏转。主应力的偏转必然导致巷道受力状态发生改变，改变后的巷道受力状态如图3(b)所示。区域主应力场偏转后，主平面相应发生偏转，模型X、Z面均会出现剪应力。在进行数值模拟给模型加载时，通常将应力加载到模型边界上，即模型的X、Y、Z面上，因而计算各个面上的应力状态就非常必要。

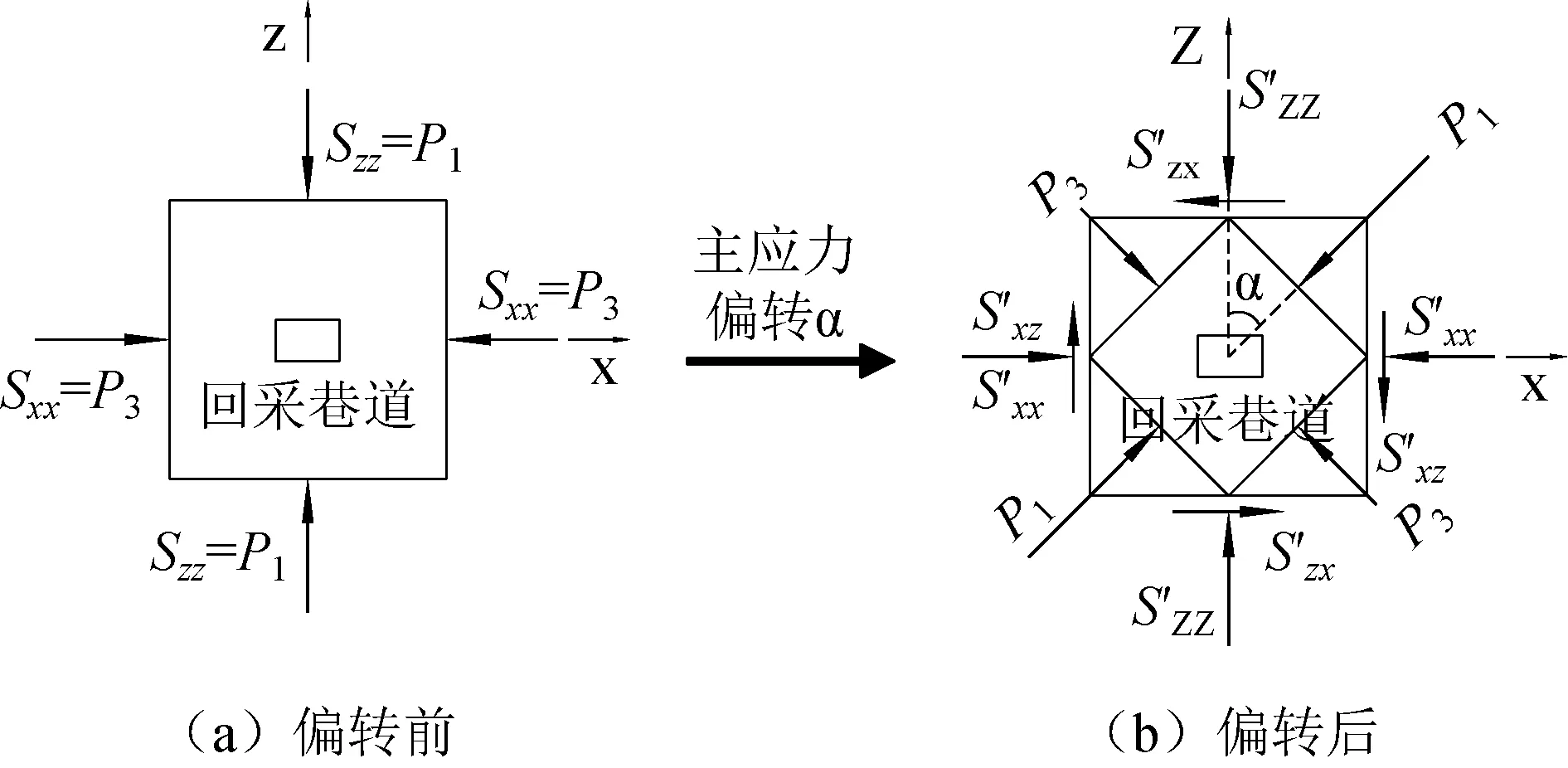
图3 区域主应力场偏转前后巷道受力分析

根据材料力学中莫尔应力圆方程，可得偏转角度为α时主应力P1、P3与X、Z面应力的关系式：

(2)

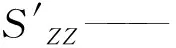
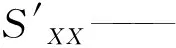
将式(2)变换得区域主应力场偏转α角度后X、Z面应力表达式：

(3)

在区域主应力场偏转前后巷道轴向平面应力状态没有发生变化，Y面仍为主平面。结合式(1)和式(3)可得回采巷道数值模拟边界加载条件表达式：

(4)

4 数值模拟分析

根据赵固二矿11071工作面运输巷的工程地质条件，采用FLAC3D建立的三维数值计算模型，破坏准则采用M-C模型。模型中岩层划分按照实际所处层位划分，其几何尺寸为50 m×1 m×55 m，计算模型共20800单元和262305个节点。模型加载时，巷道埋深取700 m，围岩泊松比取0.4，岩石容重取2.5 kN/m3，K取2。将各参数代入式(4)中，计算结果见表1。岩石力学参数如表2所示。数值模拟结果如图4所示。

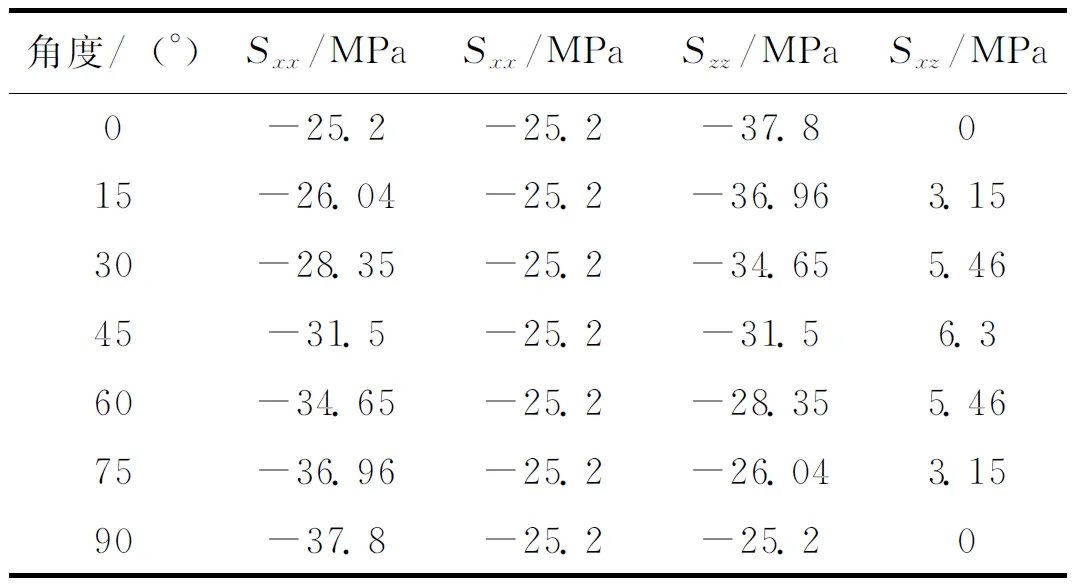
表1 主应力不同偏转角度下的加载条件

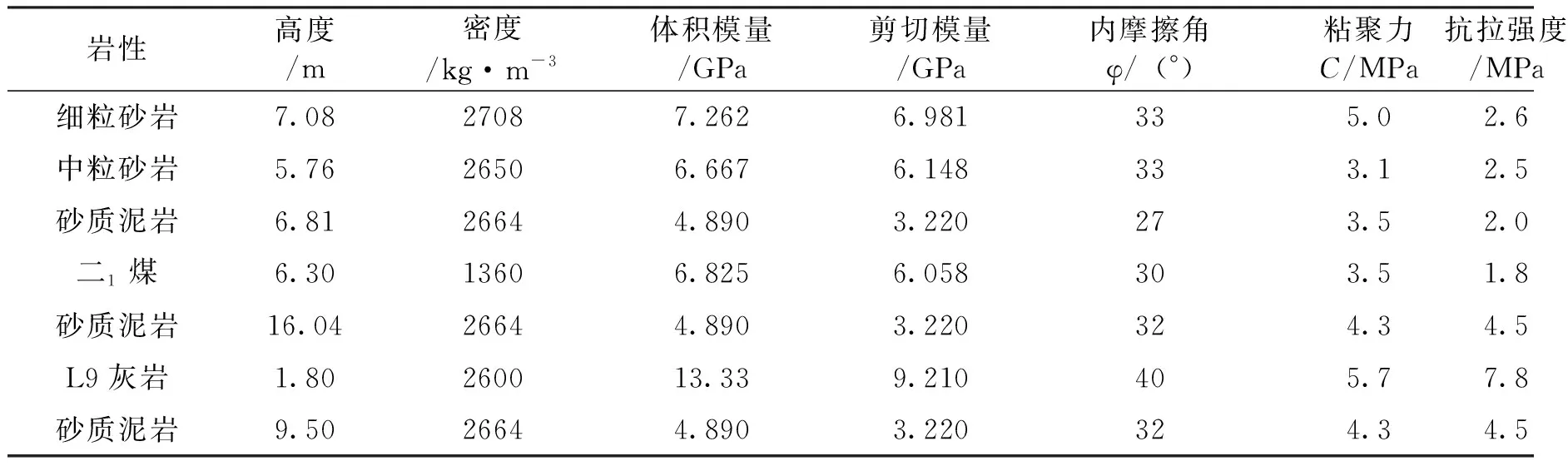
表2 岩石力学参数

图4 不同偏转角度下巷道围岩塑性区范围

由图4可以看出，当区域主应力场未发生偏转时，顶板中央位置的塑性区破坏深度为0.5 m，顶板两侧的破坏深度为1.5 m,底板破坏情况同顶板类似,两帮破坏深度接近，塑性区范围均为拱状，两帮塑性区中部最大破坏深度为2.0 m。此时破坏主要发生在两帮以及顶底板两侧，巷道围岩塑性区整体呈对称分布。

当区域主应力场偏转15°时，相比于未偏转时的塑性区形态，顶板中央位置的塑性区破坏深度增加为1 m，顶板左侧(靠近实体煤)塑性区破坏深度减少0.25 m，右侧(靠近煤柱)塑性区破坏深度增大0.25 m；底板左侧塑性区破坏深度增大0.25 m，右侧塑性区破坏深度减小0.25 m；两帮最大破坏深度未发生变化，但右帮形态与标准拱状出现偏差，右帮上部塑性区大于下部塑性区深度。此时破坏主要发生在两帮及左侧底板和右侧顶板，巷道围岩塑性区形态不再呈对称分布。

当区域主应力场偏转30°时，顶板左侧破坏深度明显小于右侧，左侧破坏深度为0.5～1 m，右侧破坏深度为1.75 m；底板左侧破坏深度明显大于右侧，左侧破坏深度为2 m，右侧破坏深度为0.5～0.75 m；左帮仍为拱状，但右帮上部塑性区深度为1.75 m，大于下部塑性区深度0.75～1.5 m。此时破坏主要发生在两帮及左侧底板和右侧顶板。

当区域主应力场继续偏转至45°时，与偏转30°时的塑性区形态相比，尽管顶底板和两帮的最大破坏深度没有增加，但是顶底板的塑性区范围明显扩大，两帮塑性区范围有所减小，顶板塑性区明显表现为左低右高，底板则表现为左深右浅。围岩塑性区形态表现为明显的不对称性。此时顶底板破坏加重，两帮破坏减少，但破坏仍然发生在两帮及左侧底板和右侧顶板。

当区域主应力场偏转至60°时，与偏转45°时的塑性区相比，顶板最大破坏深度小幅度增大至2.25 m，但形态由左低右高逐渐向拱状发展；底板最大破坏深度增大至2.5 m，同样由左深右浅向拱状发展；左帮塑性区范围进一步减小，最大破坏深度为1.5 m，右帮塑性区范围明显减小，最大破坏深度减小至1.25 m。此时两帮的破坏减少，顶底板破坏加重。

当区域主应力场偏转至75°时，顶底板与两帮塑性区范围均有所减小，顶底板最大破坏深度均为2 m，且形态均类似拱状；两帮上下部破坏深度差值减小，左帮塑性区最大破坏深度为1 m，右帮为0.75 m。此时破坏主要发生在顶底板岩层。

当区域主应力场偏转90°时，顶底板塑性区形态均为拱状，最大破坏深度为2 m；两帮塑性区形态均为梯形状，最大破坏深度均为1 m。此时破坏主要发生在顶底板岩层中，巷道塑性区形态呈明显对称分布。

综合上述分析，在区域主应力场偏转不同角度时，巷道塑性区分布形态随之发生改变，导致塑性区最大破坏深度处于巷道围岩的不同位置。因此，区域主应力场偏转角度的不同影响巷道围岩出现不同的变形特征。在区域主应力场偏转0°～90°时，随着偏转角度的增大，围岩塑性区形态由明显的对称分布逐渐变为非对称分布，之后再次趋于对称。在区域主应力场偏转小于30°时，两帮的破坏程度大于顶底板，顶板塑性区主要分布在煤柱侧，底板塑性区主要分布在煤壁侧。在区域主应力场偏转30°～45°之间时，顶底板塑性区范围增大，但两帮的破坏程度仍略大于顶底板。在区域主应力场偏转45°～60°之间时，两帮与顶底板最大破坏深度相当，顶板最大破坏深度由煤柱侧向顶板中部发展，底板最大破坏深度由煤壁侧向底板中部发展。在区域主应力场偏转60°～90°之间时，破坏主要发生在顶底板，两帮塑性区范围不大。

因此，通过以上分析可以发现，赵固二矿11071工作面运输巷围岩变形破坏特征与区域主应力场的偏转有关。当巷道围岩区域主应力场偏转角度在45°～60°之间时，该巷道出现两帮收敛量与顶底板移近量接近、煤柱侧顶板下沉严重、煤壁侧底板底臌量较大的变形特征，如图5所示。

图5 回采巷道围岩非对称变形破坏特征

5 结论

(1)将材料力学中的莫尔应力圆方程应用到巷道区域主应力场的计算中，推导出了回采巷道考虑区域主应力场偏转的数值模拟边界加载条件表达式。

(2)赵固二矿11071工作面运输巷非对称变形与区域主应力场的偏转有关。通过数值模拟分析发现，区域主应力场偏转角度的不同影响巷道围岩出现不同的变形特征，当巷道围岩区域主应力场偏转角度在45°～60°之间时，该巷道出现非对称变形特征。