“过山车”模型的前世今生

湖北

徐 进

过山车是游乐场的常见设施，乘坐过山车可以体会运动的惊与险，为了确保游客的生命安全，需要设计者对各种情况进行精心设计、准确计算。为了使学生能初步解决这类问题，人教版必修2第80页专门设计了一道相关习题，平时考试中也常以过山车为载体考查圆周运动中的各种情况。为此，笔者对此类模型的前世今生进行归纳、总结、拓展。

【教材母题】游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来，如图1。我们把这种情况抽象为如图2的模型：弧形轨道的下端与竖直圆轨道相接，使质量为m的小球从A点沿弧形轨道上端滚下，小球进入圆轨道下端B点后沿圆轨道运动。实验发现，只要h大于一定值，小球就可以通过圆轨道的最高点。如果已知圆轨道的半径为R，h至少要等于多大？不考虑摩擦等阻力。

小球从A点运动到最高点C的过程中，只有重力做功，由机械能守恒定律得：

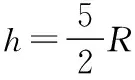
为了更透彻地理解“过山车”模型，需要将其前世进行还原。

【模型前世情景还原1】如图3所示为游乐场中过山车的一段轨道，P点是这段轨道的最高点，A、B、C三处是过山车的车头、中点和车尾。假设这段轨道是圆轨道，各节车厢的质量相等，过山车在运行过程中不受牵引力，所受阻力可忽略。那么过山车在通过P点的过程中，下列说法正确的是 ( )

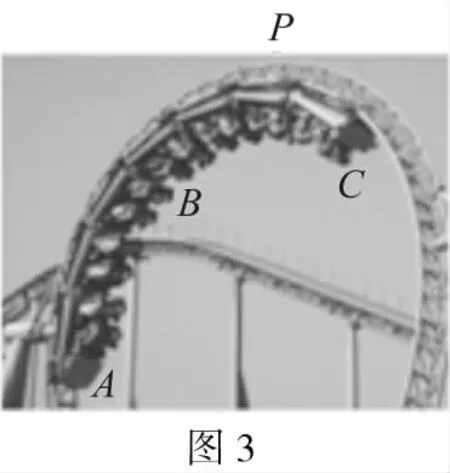
A．车头A通过P点时的速度最小

B．车的中点B通过P点时的速度最小

C．车尾C通过P点时的速度最小

D．A、B、C通过P点时的速度一样大

【解析】过山车在运动过程中，受到重力和轨道支持力作用，只有重力做功，机械能守恒，动能和重力势能相互转化，则当重力势能最大时，过山车的动能最小，即速度最小，根据题意可知，车的中点B通过P点时，重心的位置最高，重力势能最大，则动能最小，速度最小，故B正确。

【模型前世情景还原2】如图4所示，露天娱乐场空中列车由许多节完全相同的车厢组成，列车先沿光滑水平轨道行驶，然后滑上一固定的半径为R的空中圆形光滑轨道，若列车全长为L(L>2πR)，R远大于一节车厢的长度和高度，那么列车在运行到圆形光滑轨道前的速度至少要多大，才能使整个列车安全通过固定的圆形轨道(车厢间的距离不计)。

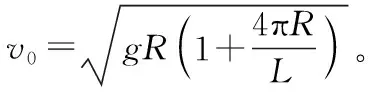
弄懂“过山车”模型的前世是解决这类问题的前提，拓展其今生、应用其今生是关键。

【模型今生拓展1】如图5所示，竖直平面内光滑圆轨道半径R=2 m，从最低点A有一质量m=1 kg的小球开始运动，初速度v0方向水平向右，重力加速度g取10 m/s2，求：

【无惊无险】(1)小球做往复运动的条件；

【有惊无险】(2)小球做圆周运动的条件；

【危险事例】(3)若初速度v0=8 m/s，求小球离开圆轨道时的高度及速度大小。

【解析】(1)当小球恰好运动到与圆轨道中心等高处时，

(2)当小球恰好能到达最高点时，由重力提供向心力，此时速度最小，有：

从A到B的过程中，根据动能定理得：

解得：v0=10 m/s

所以小球能到达最高点B的条件是：v0≥10 m/s。

根据几何关系得：

所以离开圆轨道的位置离A点的距离为H=R+h=2.8 m。

【模型今生拓展2】如图6所示，水平的粗糙轨道与竖直的光滑圆形轨道相连，圆形轨道间不相互重叠，即小球离开圆形轨道后可继续沿水平轨道运动。圆形轨道半径R=0.2 m，右侧水平轨道BC长为L=4 m，C点右侧有一壕沟，C、D两点的竖直高度h=1 m，水平距离s=2 m，小球与水平轨道间的动摩擦因数μ=0.2，重力加速度g取10 m/s2。小球从圆形轨道最低点B以某一水平向右的初速度出发，进入圆形轨道。

(1)若小球通过圆形轨道最高点A时给轨道的压力大小恰为小球的重力大小，求小球在B点的初速度大小；

(2)若小球从B点向右出发，在以后的运动过程中，小球既不脱离圆形轨道，又不掉进壕沟，求小球在B点的初速度大小的范围。

从B到A过程，由动能定理可得：

(2)情况一：若小球恰好停在C处，对全程进行研究，由动能定理可得：

解得：v1=4 m/s

小球刚好通过最高点A时，有：

从B到A过程，则有：

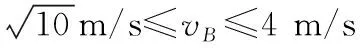
情况二：若小球恰能越过壕沟，则有：

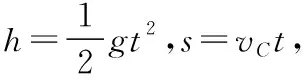
所以当vB≥6 m/s，小球越过壕沟。

情况三：若小球刚能运动到与圆心等高位置，则有：

得v4=2 m/s

所以当vB≤2 m/s时，小球又沿圆轨道返回。综上，小球在B点的初速度大小的范围是：

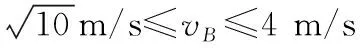
(1)小球在从P开始运动到C点过程中的最大动能；

(2)要使小球在圆轨道上运动的过程中不脱离圆轨道，释放点P离B点的距离应该为多少？

【解析】(1)设小球通过C点时的速度为vC，根据牛顿第二定律得：

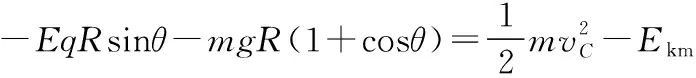
故小球在从P开始运动到C点过程中的最大动能为：

(2)由第(1)问可知，要使小球不脱离轨道，距离足够远，能过C点；则

由动能定理，小球从释放到C点有

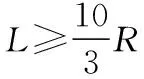
距离较近，沿轨道返回，设最高点为M点，如图8所示，由分析可知，M点合力方向垂直OM，小球从释放到M点，由动能定理可得：

Eq(L+Rcosθ)-mgR(1+sinθ)≤0