基于自适应模糊器的飞行器轨迹跟踪控制

马耀名 吕玉恒

(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125100)

0 引 言

旋翼类飞行器能够进行垂直起降、悬停、曲线循迹[1-2]等多种复杂的空间运动，具有快速性、灵活性、精准性等特点。近几年，飞行器空前巨大的市场前景而备受学者的关注。

飞行器可进行遥控和自主飞行，并具有较好的精确性、快速性、抗干扰性等特点。飞行器具有两种空间坐标系六种相关联的自由度，却只有四种控制输出，是典型的欠驱动系统[3]，其具有多输入多输出、非线性、强耦合等特点，采用模糊、自适应、观察器、滑模控制、内外双闭环等控制算法[4-10]。

文献[11]采用双闭环滑模控制系统，并在外环自适应、内环加入干扰观测器，使飞行器具有较好的抗干扰性和跟踪精度。

文献[12]针对飞行器惯性参数不确定的情况，提出了一种滤波补偿的参数不确定自适应轨迹跟踪控制。在位置、姿态控制器的基础上添加了线性微分跟踪器以及惯性参数估计器，基于输入输出位置、姿态稳定性理论构造的控制律和惯性参数估计律，导出的姿态信号再运用线性微分跟踪器进行指令动态补偿，避免了轨迹跟踪控制对时标分离的依赖。

文献[13]针对带有模型参数不确定和风微扰状况,提出了一种全局动态鲁棒性控制策略,设计了模型预测控制器来实现直线运动部分的动态实时控制。引入全局鲁棒滑模控制方法,来稳定四旋翼飞行器在参数不确定和风微扰情况下的旋转姿态行为和直线运动。

飞行器多进行户外勘测，考虑到近地效应、桨叶挥舞、阵风等外界干扰的影响，对多种力学模型的对比分析[14-18]，采用欧拉-拉格朗日动力学模型，因此飞行器必须具有抗外界干扰的鲁棒性。本文设计了基于滑模自适应控制的轨迹跟踪自适应控制算法，提高了系统的灵敏度，完成了高精度的轨迹跟踪控制。

1 飞行器运动模型

如图1所示，四旋翼飞行器由十字交叉的四个直流无刷电机提供动力，通过改变螺旋桨的转速进而完成飞行器的升降、翻滚、航偏等飞行动作。同时飞行器的空间运动将通过惯性坐标系转换到刚体坐标系的姿态角变换上，如当W1≠W3,W2=W4将进行俯仰，W2≠W4,W1=W3时将进行翻滚，W1=W3≠W2=W4时进行航偏，当W1～W4之和垂直方向的升力与重力的大小决定升降变换。

图1 四旋翼飞行器结构图

如图1所示，建立飞行器在惯性系下受力、位置、加速度之间的等式关系。在刚体坐标系下的角度、角加速度、转矩之间的等式如下[11]：

(1)

(2)

(3)

式中：C( )和s( )分别代表余弦函数、正弦函数。

J是刚体惯性张量I在惯性坐标系中的表示:

(4)

C为科里奥及离心力项[19],计算公式为：

(5)

dF=[dx,dy,dz]T,dΓ=[dφ,dθ,dψ]T分别代表气流对飞行器的干扰力和干扰力矩。

Fi为各个电机所产生的升力：

(6)

(7)

由于空气阻力螺旋桨产生的反转力矩为:

(8)

Γ为系统中间控制输入:

(9)

2 控制器设计

如图2所示，飞行器的控制系统可分为三部分：(1) 控制信号发生器；(2) 外环位置子系统自适应控制器和姿态子系统控制；(3) 位置和姿态子系统。发生器产生飞行器所期望的飞行轨迹的位置和ψ期望姿态角，经由外环位置控制器产生θ、φ期望姿态角，并传递给内环姿态控制器由内环消除外环误差；位置和姿态子系统用来产生新的位置和姿态角等信息并反馈给位置控制形成闭环。

图2 四旋翼飞行器系统结构图

2.1 位置控制器及其子系统的设计

定义跟踪误差为：

ep=p-pd

(10)

由式(1)、式(9)可得位置子系统的误差方程：

(11)

式中：

UP=U1Re3

(12)

(13)

设计控制器UP：

(14)

(15)

将式(11)、式(14)代入式(13)得：

(16)

Lyapunov函数为：

(17)

(18)

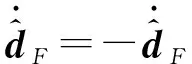
(19)

把式(16)、式(18)、式(19)代入式(17)得:

(20)

通过虚拟控制输入Up计算实际的升力U1和姿态子系统中间指令信号Θd。

由式(3)可将Up=U1Re3可写成：

Upx=U1(CφSθCψ+SφSψ)

(21)

Upy=U1(CφSθSψ-SφCψ)

(22)

Upz=U1CφCθ

(23)

把式(23)分别代入式(21)、式(22)进行组合变换可得俯仰、翻滚的期望角及实际的位置控制器U1：

(24)

(25)

(26)

2.2 姿态控制器设计

航偏角信号ψd为给定的指令信号，与位置跟踪系统产生的俯仰、翻滚的期望角，作为姿态控制器的期望，用于消除角度误差，同时考虑到模型的不确定性和外界非结构性干扰力矩的影响，可将式(2)变为：

(27)

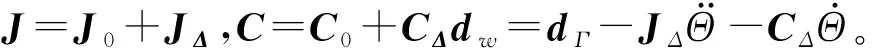
跟踪误差信号:

(28)

滑模函数为:

(29)

由式(26)、式(28)可得姿态误差子系统：

(30)

设计姿态控制器为：

(31)

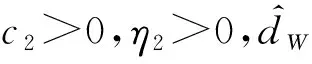
设计模糊自适应控制器，降低干扰的影响。

式中：NB为负大，NM为负中，ZO为零，PM为正中，PB为正大。

1.5}，子集中两边是高斯隶属函数，中间是三角隶属函数，如图3和图4所示。

图3 φ姿态角模糊输入的隶属函数

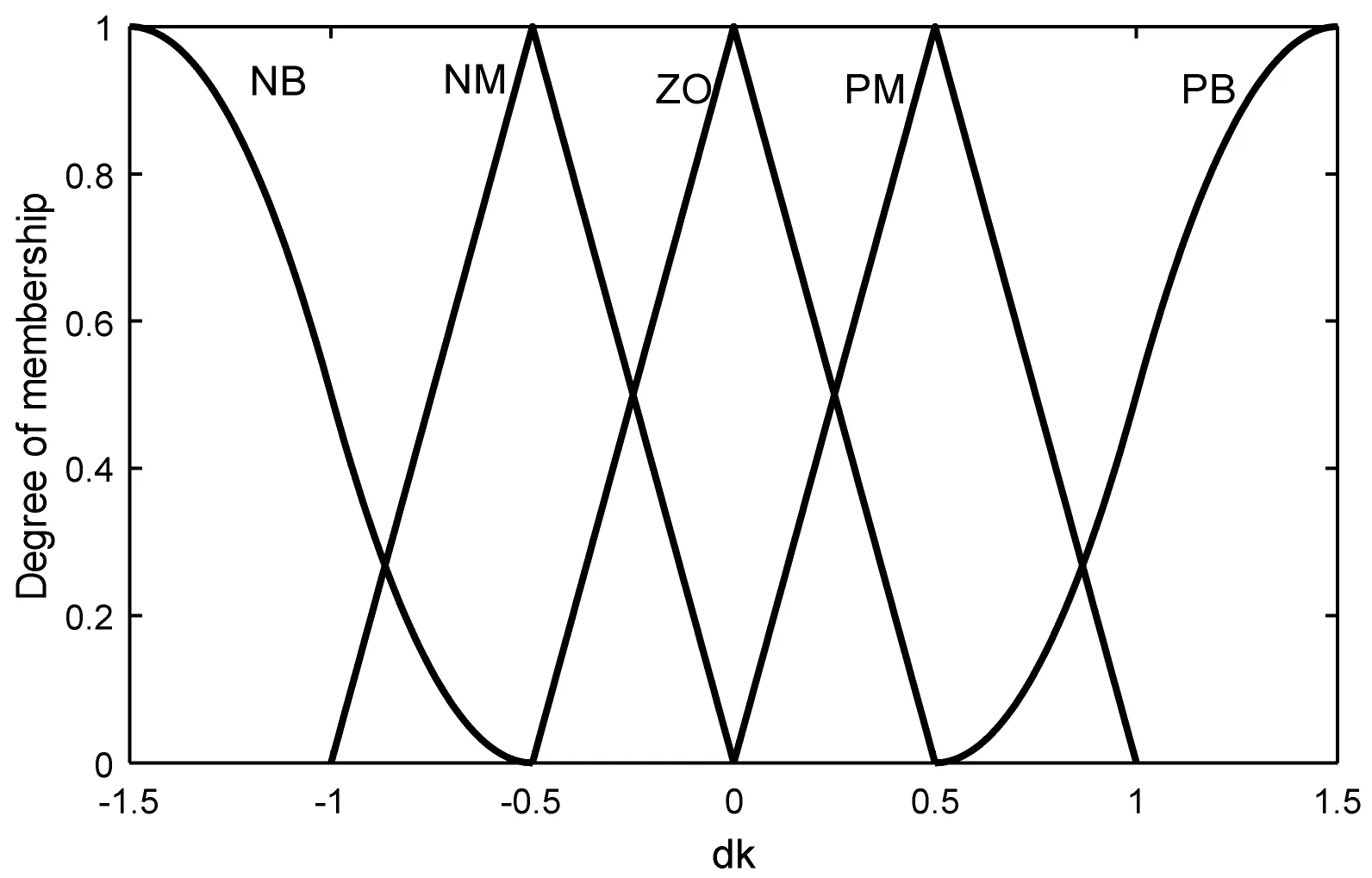
图4 φ姿态角模糊输出的隶属函数

模糊规则设计如下：

模糊输出的表达式为：

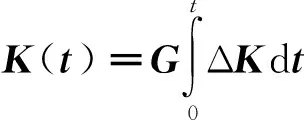
(32)

(33)

(34)

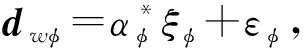
同理转变成三维姿态角的对应向量。

(35)

(36)

(37)

定义干扰估计误差:

(38)

(39)

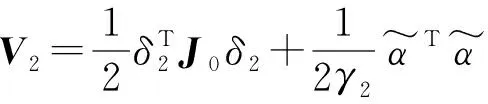
(40)

(41)

把式(30)、式(31)、式(38)、式(41)代入式(40)得:

(42)

当η2>ε,由式(36)可得：

(43)

姿态子系统稳定。

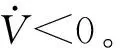
3 仿真及结果分析

I=diag(0.004,0.004,0.008)

半径为L=0.5 m,气动干扰力：

dF=[0.2sin(0.1πt),0.2cos(0.1πt),

0.2cos(0.1πt)]

干扰力矩为：

dΓ=[0.3sin(0.1πt)+0.1,0.4cos(0.1πt)+0.1,0.5sin(0.1πt)+0.2]

位置控制器参数为:

利用Matlab仿真软件，在Simulink中建立系统模型，在s函数中编写各个模块的程序，设计进行30 s的仿真。

仿真结果如图5-图8所示。

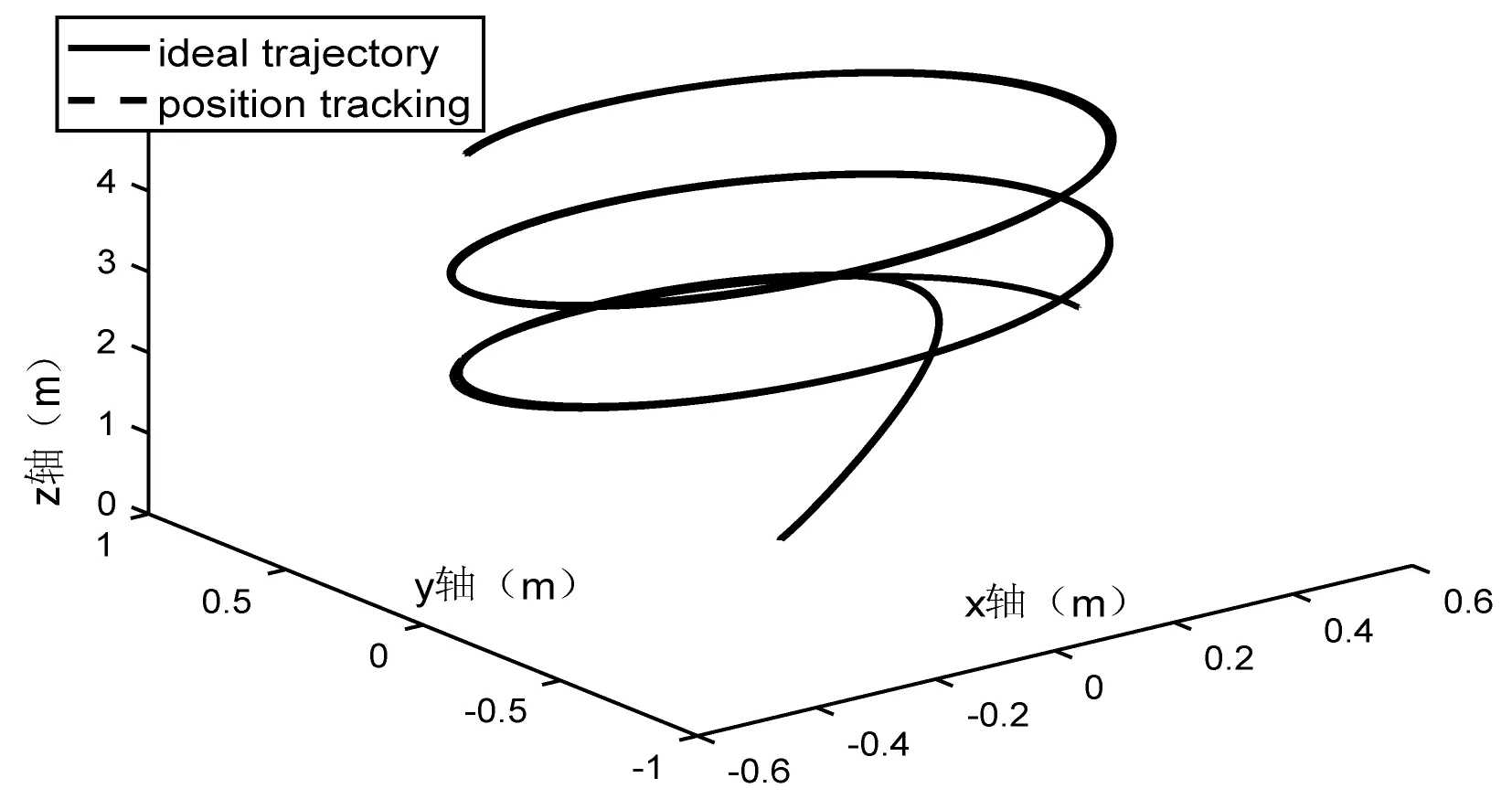
图5 三维轨迹

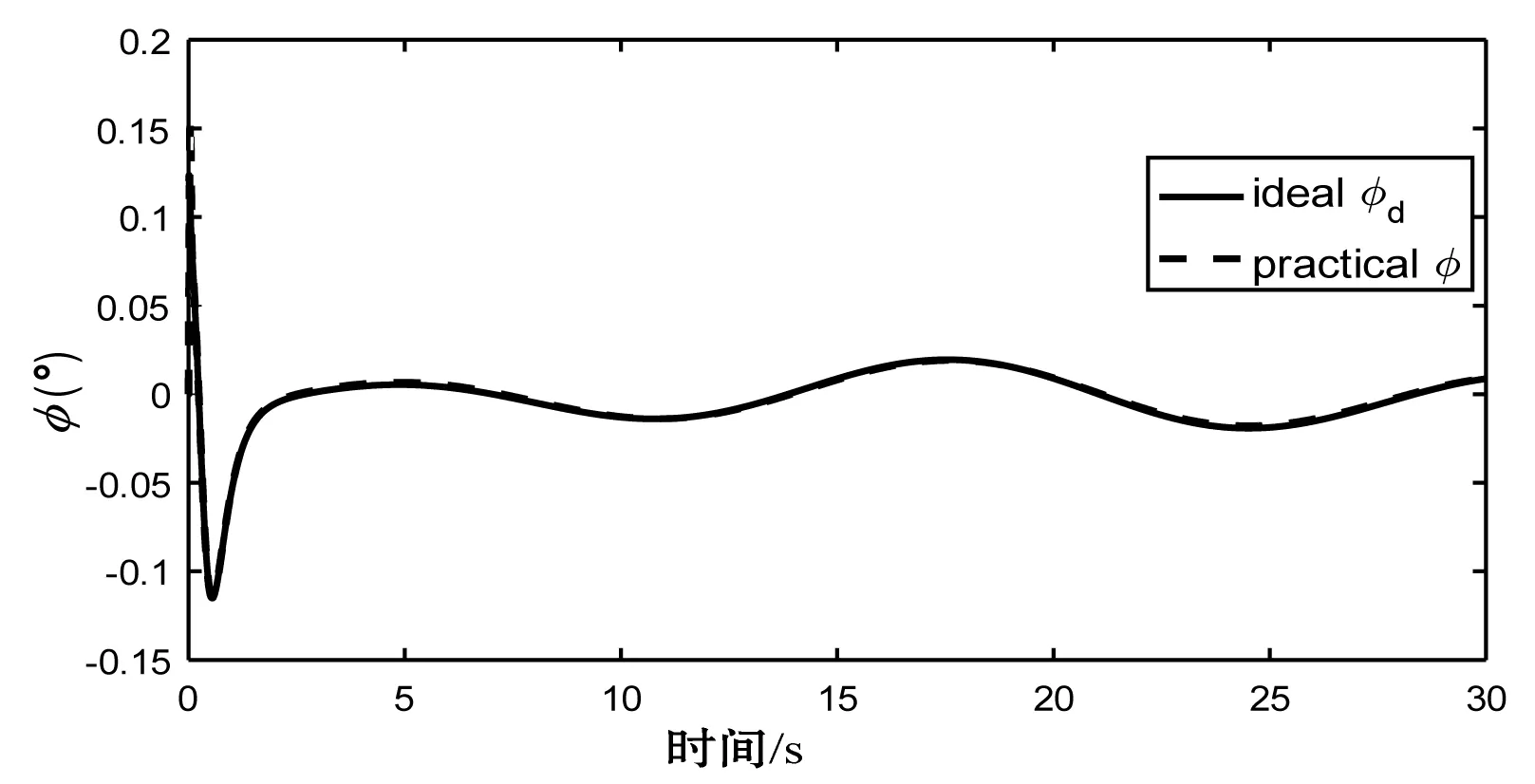
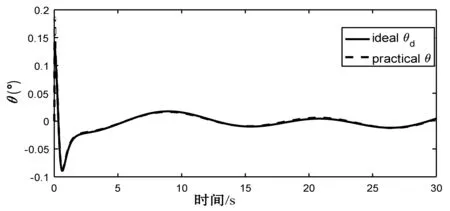
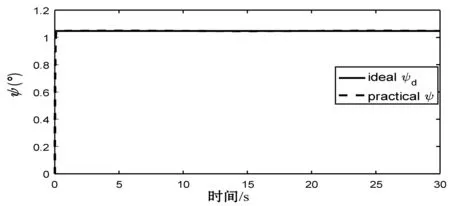
图6 姿态角输出

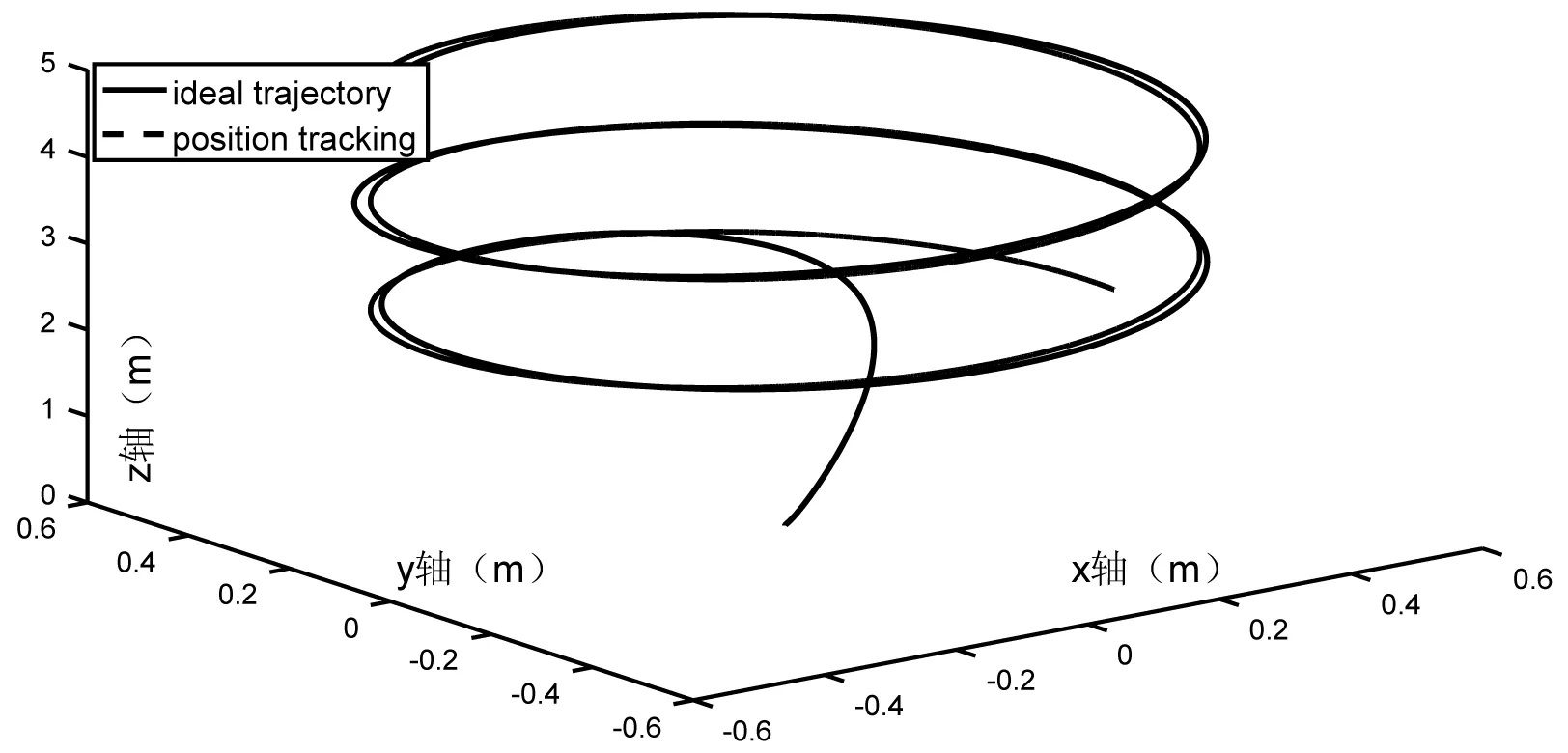
图7 对比算法的三维轨迹

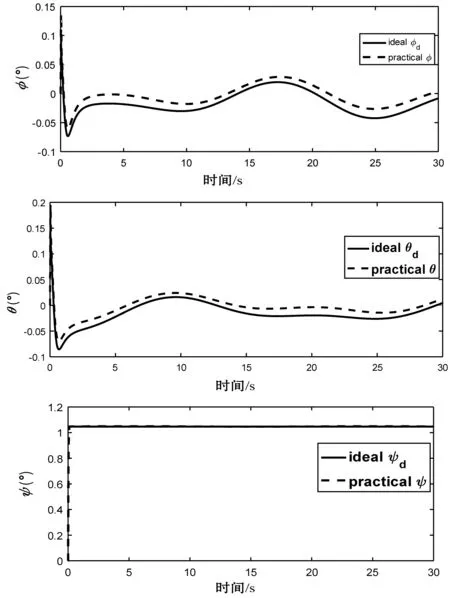
图8 对比算法的姿态输出

图7、图8为对比算法的仿真，和本文有相同的力学模型、系统结构和控制算法参数，同样采用了内外双闭环滑模控制算法，但位置控制器没有添加自适应控制律和姿态环没有加入模糊自适应控制律，其他控制器参数与本文都相同。

从图5、图7对比可以看出，图5在1.7 s时趋于稳定，图7在2.5 s时趋于稳定，说明加入算法后提高了飞行器的快速性。且仿真期间，在加入干扰的情况下，图7的x、y轴存在上下2 cm的误差，而(图5)改进算法后将误差缩小到了0.2 cm。从图6、图8的对比中可以看出，模糊自适应算法提高了姿态角控制器的跟踪中间信号的精度。

4 结 语

针对轨迹跟踪类飞行器，设计一种高精度的自适应算法，通过自适应控算法，减少外界干扰的影响；并设计一种模糊自适应算法，进一步地消除气动干扰和转动惯性误差等，从而减少滑膜抖振的影响。理论分析和仿真都表明，所设计的控制器具有较好的稳定性和抗干扰能力,这种基于模糊自适应控制策略对于飞行器克服外界及转动干扰具有较好的参考意义。