一种准平稳相干信号的DOA估计算法

张辰锐 王剑书 雷 涛

1(吕梁学院物理系 山西 吕梁 033000) 2(西北工业大学电子信息工程学院 陕西 西安 710129) 3(陕西科技大学电气与信息工程学院 陕西 西安710021) 4(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)

0 引 言

波达方向估计(DOA)是阵列信号处理的一项重要课题，并且广泛应用于雷达、声呐和通信等领域[1-3]。从多重信号分类(MUSIC)算法[4]提出开始，国内外学者对平稳信号的子空间高分辨DOA算法进行了深入的研究。本文的兴趣在于准平稳信号QSS(Quasi-stationary signals)的DOA估计算法研究。准平稳信号是统计量在一定短时间内保持不变但会随着时间片段变化的一类信号[5]，例如:语音、音乐和一些机械信号通常被认为是准平稳信号。机场鸟声监测，麦克风阵列和地面声目标监测等环境都有QSS的DOA估计的实际应用，从而受到广大学者的重视。

2010年，Ma等[5]提出一种针对QSS的Khatri-Rao(KR)子空间的方法，该方法利用QSS信号的短时平稳的特点，构造了新的数据模型，获得了比普通MUSIC算法更高的角度分辨率。方法中提出的协阵列(co-array)的概念、对于非均匀线阵nested array[6-7]、co-preme array[8-9]等以及基于高阶累积量(HOC)的DOA估计[7]都具有重要的意义。然而，当信号源相干时，源信号的协方差矩阵不再为对角矩阵，KR子空间模型的构造将失效。对于相干源的DOA估计问题，前人也进行了深入的研究。20世纪80年代，Shan等[10]提出了空间平滑(SS)方法，通过缩小均匀线阵有效阵列孔径，解决了相干源导致的协方差矩阵秩缺失的问题。前后向空间平滑(FBSS)的发展扩大了SS方法的阵列孔径，提升了自由度[11-12]。2005年，Han等[13]提出一种通过构造Toeplitz矩阵并利用类旋转不变技术(ESPIRIT)的方法求解的DOA估计方法。2007年，Ye等[14]对此进行改进，重新构造了矩阵模型，提升了自由度。2010年，Choi[15]通过特征向量方法(EVM)和相关向量方法(CVM)分别构造前向后向向量，并使用类ESPIRIT方法求解DOA，其中EVM方法在全相干源环境下具有很好的效果。上述相干源DOA估计方法一般假设源信号为平稳信号，噪声为不相关的高斯白噪声，实际环境中，噪声可能包含部分干扰源信号，可能具有一定的相关性，这将导致上述相干源DOA估计算法的性能下降。

本文针对准平稳相干源和相关噪声的环境，提出一种基于KR子空间和前后向空间平滑(FBSS)的DOA估计方法。该方法首先利用接收信号各帧的协方差矩阵构造Toeplitz矩阵，然后将这些矩阵利用KR子空间方法构造一个新的模型，最后利用FBSS方法进行DOA估计。同时，该方法将非相干子空间处理(ISSM)方法[15]进行了扩展，可进行宽带阵列信号模型的准平稳相干信号的DOA估计。仿真实验表明，本文方法具有较高的检测概率和较低的均方根误差(RMSE)，同时也验证了本文方法对于宽带阵列信号模型的有效性。

1 窄带阵列信号模型

考虑由2N+1个各向同性的阵元组成的均匀线阵，其阵元位置记为-N,-N+1,…,0,…，N。假设存在K个远场窄带信号源入射到上述阵列，源信号记为s(t)=[s1(t),s2(t),…,sK(t)]T，阵元接收到的信号记为x(t)=[x-N(t),x-N+1(t),…,xN(t)]T，阵元接收的噪声为v(t)=[v-N(t),v-N+1(t)，…,vN(t)]T，则接收信号模型为：

x(t)=As(t)+v(t)

(1)

式中:A=[a(θ1),a(θ2),…,a(θK)]为阵列流型矩阵，a(θk)=[e-j2π(-N)d sinθk/λ,e-j2π(-N+1)d sinθk/λ,…,e-j2πNd sinθk/λ]T,θk为第k个信号的来向，λ为源信号的波长，d为均匀线阵的阵元间距，且等于源信号的半波长。

这里对源信号与噪声作如下假设：

1) 假设源信号的数目已知，且每个信号的来向不一样。

2) 假设源信号为准平稳信号，且各个源信号之间可能相干。

3) 假设噪声信号为平稳信号，与各个源信号不相关，但各阵元接收的噪声信号可能具有相关性。

由于源信号为准平稳信号且相干，噪声相关，传统的相干源DOA估计算法的性能可能会下降甚至失效。

2 算法描述

2.1 帧内处理

对接收信号x(t)按采样后的数据长度L进行分帧，认为帧内信号为平稳信号，则第m帧的信号的协方差矩阵为：

Rx,m=E{xm(t)xm(t)H}=ARs,mAH+C

(2)

式中：Rs,m为第m帧内源信号的协方差矩阵，C为噪声信号的协方差矩阵。使用Rx,m的第n行元素构造Toeplitz矩阵：

(3)

式中：n=-N,-N+1,…,N，则上式可以写为：

Wn,m=ArDn,mArH+Cn

(4)

式中：Ar=[ar(θ1),ar(θ2),…,ar(θK)]为阵元0,1，…,N组成的子阵列流型，ar(θk) = [1,e-j2πd sinθk/λ,e-j2πNd sinθk/λ]T，Dn,m为矩阵ARs,m的第n行元素构成的对角矩阵，Cn如下：

(5)

式中：C(n1,n2)为C在(n1,n2)位置的元素，n1,n2=-N,-N+1,…,N。

将协方差矩阵各行构造的Toeplitz矩阵累加起来，构造成新的Toeplitz矩阵：

(6)

2.2 DOA估计

通过KR子空间和FBSS方法进行DOA估计。首先对Wm向量化：

ym

(7)

式中：vec(·)为按列向量化运算，⊙为KR乘积[5]运算，dm=diag(Dm)。令Y[y1,y2,…,yM]，则：

(8)

式中：Ψ=[d1,d2,…,dM]，1M=[1,…,1]T∈M。

对于准平稳信号，一个普遍合理的假设：矩阵[Ψ,1M]∈M×(K+1)是列满秩的[5]。

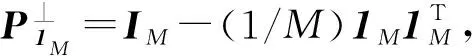
(9)

令Φ则：

Z=BΦ

(10)

式(10)与信号模型式(1)有类似的结构，将Φ的每一行视作一路源信号，将B视作阵列流型，则Z为该阵列流型下的接收信号。式(10)通过计算消除了噪声项，所以该模型不仅能处理不相关的高斯白噪声，而且对未知的相关噪声也具有很好的抑制效果。由于B其行有冗余，则Z的行也有冗余。消除Z中重复的行，并将各行按阵列流型A排列可以得到：

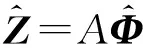
(11)

式中:E=diag[e-j2πd sinθ1/λ,e-j2πd sinθ2/λ,…,e-j2πd sinθK/λ]。则有：

(12)

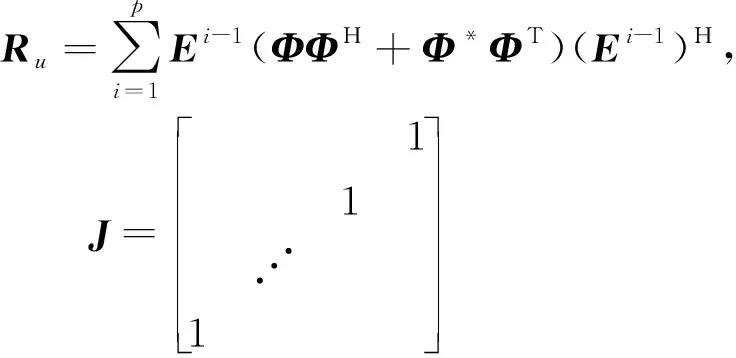
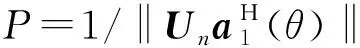
3 宽带阵列信号模型处理

准平稳信号在现实中多为宽带信号，这里提出宽带阵列信号模型的DOA方法。第n个阵元接收的信号用各个源信号的时延混合表示：

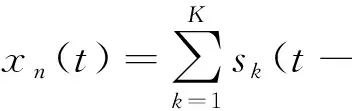
t=0,1,2,…

(13)

(14)

式中：NSTFT为短时傅里叶变换的窗口长度，f∈[-1/2,1/2]为归一化频率。对xn(t)进行STFT，并令

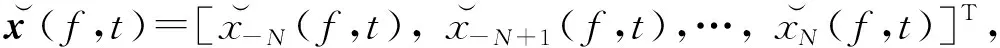
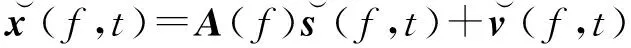
(15)

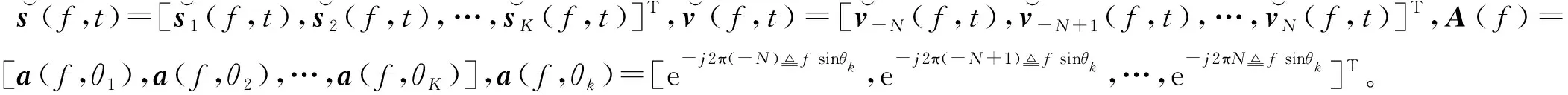
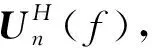
(16)

式中：f1和f2分别为处理的最小归一化频率和最大归一化频率。搜索空间谱函数式(15)谱峰位置则可得宽带源信号的来向。

4 仿真分析

4.1 窄带阵列信号模型实验

使用检测概率和均方根误差(RMSE)来对算法进行评价。定义DOA的“正确检测”：一次实验中检测到的所有的DOA值分别与其对应的真实DOA值误差不超过2°。检测概率定义为：蒙特卡洛实验中正确检测的实验次数与总实验次数的比值。RMSE定义为蒙特卡洛实验中正确检测实验的DOA估计的均方根误差：

(17)

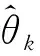
实验一：信噪比(SNR)与噪声相关系数对算法的影响。使用9元均匀线阵，N=4，源信号使用准平稳的拉普拉斯分布的信号，来向分别为-40°、-20°、0°、15°、30°、50°。各阵元添加的噪声为具有相关性的高斯白噪声。源信号每一帧长度为150，帧数为150，前5个源信号互为相干信号，第6个信号为独立信号。对于各信噪比与噪声相关系数分别进行500次蒙特卡洛实验，本文方法(记为KR-FBSS)与FBSS方法、改进的Toeplitz结构方法[13](记为TBD)、EVM和CVM方法的实验结果如图1所示。从图1可以看出，在各组相关噪声条件下，本文方法具有最好的检测概率，随着噪声相关系数增加，对比方法的检测概率下降较明显，而本文方法检测概率下降并不大。

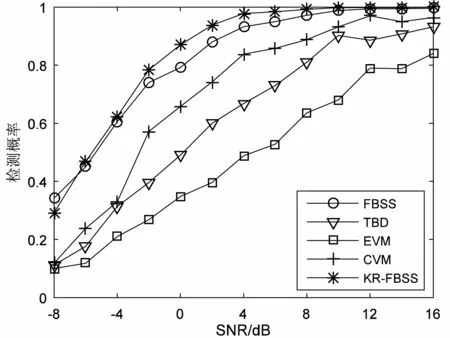
(a) 噪声相关系数0.01

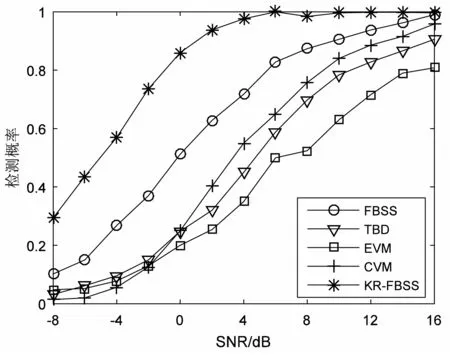
(b) 噪声相关系数0.05

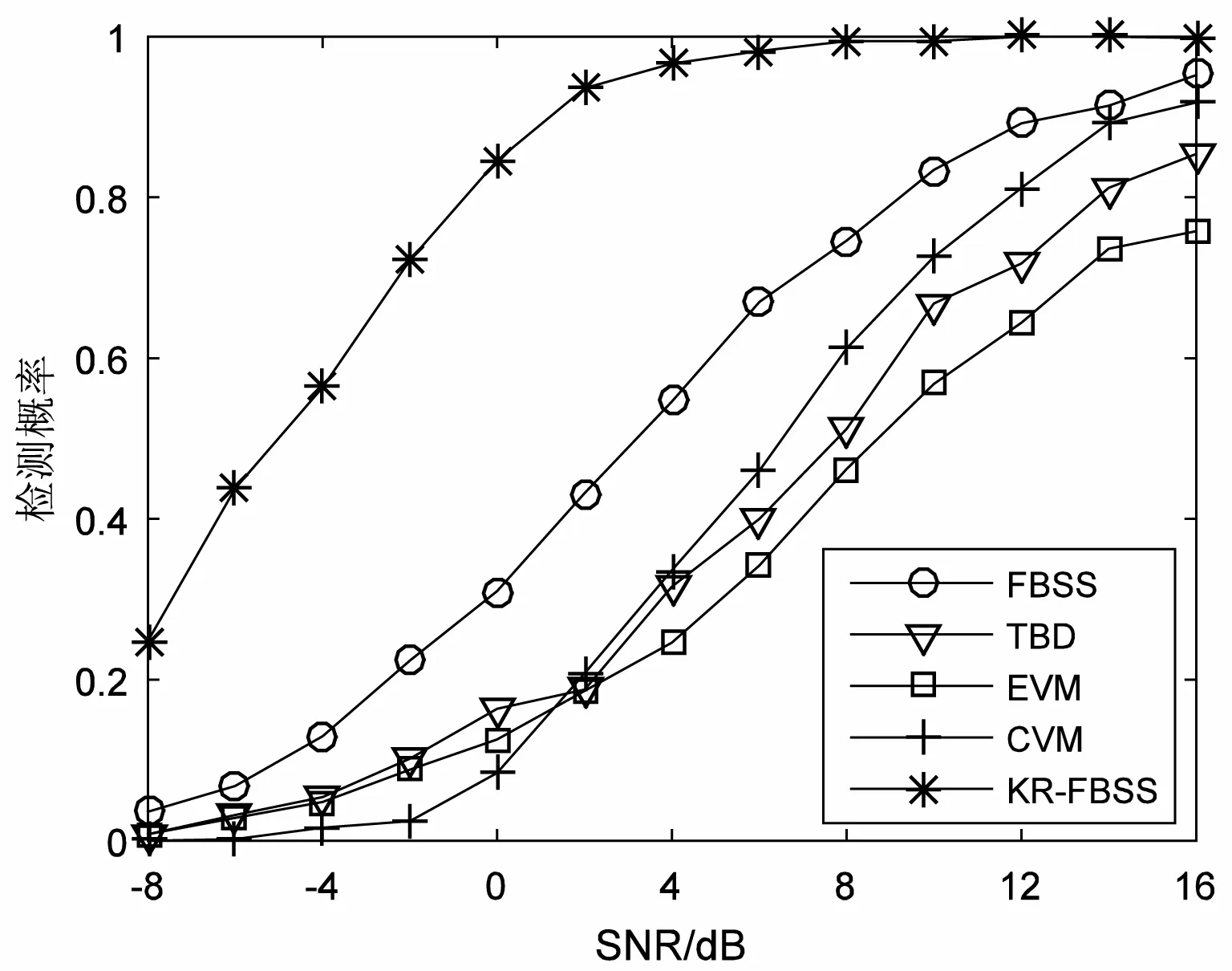
(c) 噪声相关系数0.1

(d) 噪声相关系数0.2 图1 不同信噪比和噪声相关系数下检测概率

实验二：相近的DOA值的估计性能。与实验一使用一样的阵列结构，使用两个相干的准平稳拉普拉斯分布的信号源，帧数和帧长度均为150，来向分别为3.2°和8.6°。各阵元添加噪声为相关的高斯白噪声，相关系数为0.1。在各信噪比条件下分别进行500次蒙特卡洛实验，实验结果如图2所示。可以看出，本文算法具有更高的检测概率和更好的RMSE表现。

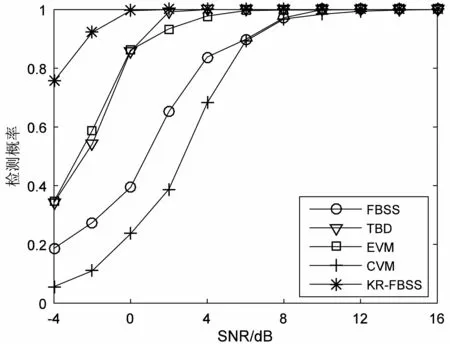
(a) 不同SNR下的检测概率

(b) 不同SNR下的RMSE 图2 相近的DOA值估计性能

实验三：分帧长度与帧数对DOA估计的影响。与实验二使用一样的阵列结构和源信号，在各阵元添加相关系数0.1的高斯白噪声噪声，SNR为6 dB，在不同相关系数和不同帧长度与不同帧数条件下分别进行500次蒙特卡洛实验，实验结果如图3所示。可以看出，随着帧长度和帧数增加，RMSE更小，为保证RMSE尽量小，帧长度和帧数目均不宜太小，同时也可以看出噪声相关系数对本文算法影响较小。

(a) 帧长度变化，帧数为150

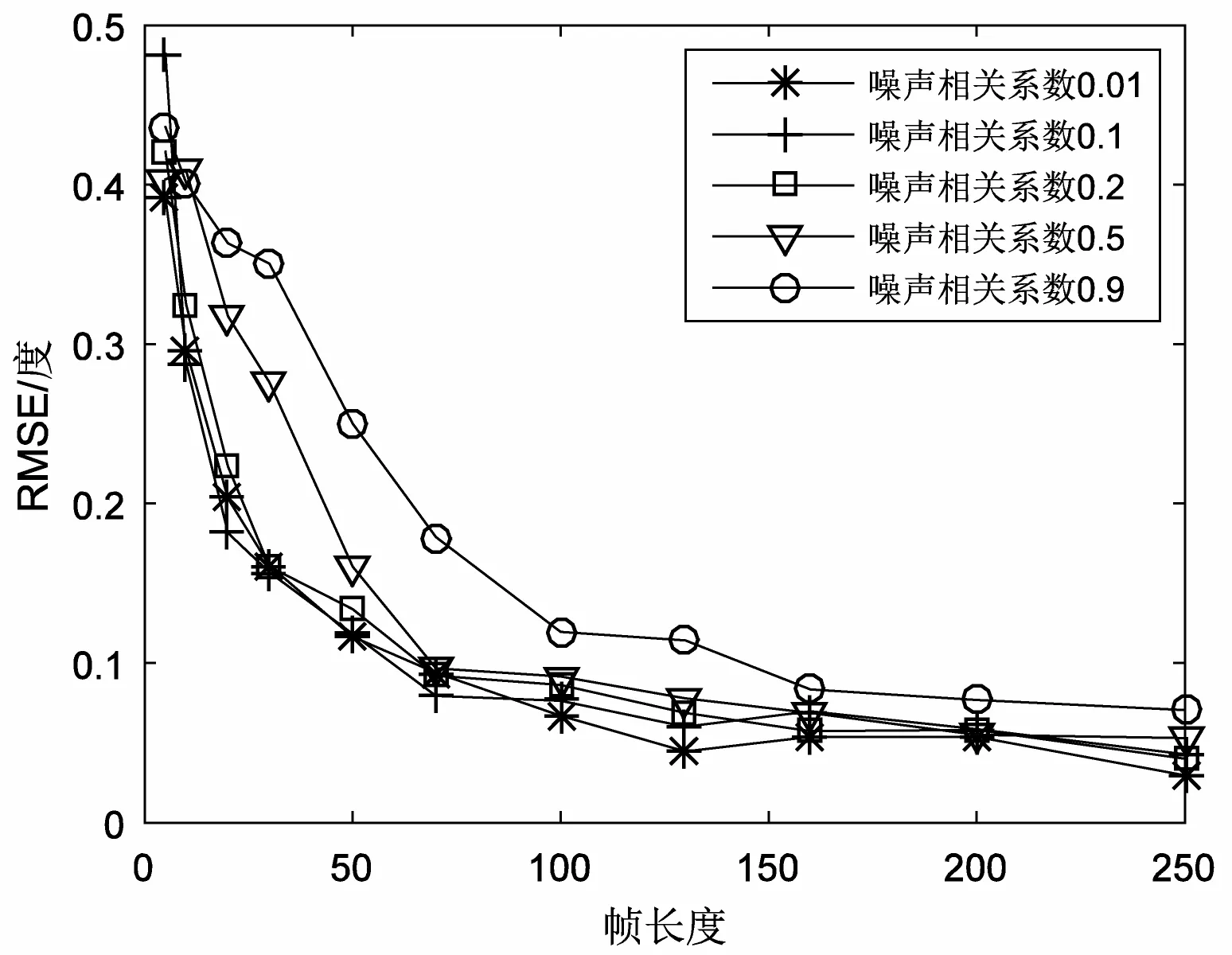
(b) 帧数变化，帧长度为150 图3 帧长度和帧数对RMSE的影响

4.2 宽带阵列信号模型实验

阵列与4.1节一致，使用4路相干的语音信号作为源信号，来向分别为-40°、-20°、0°、30°。源信号采样频率为8 000 Hz，各阵元添加信噪比为6 dB的高斯白噪声，相关系数为0.1。对比的方法为相干子空间处理方法[16](CSSM)和文献[17]的方法(CSSM-PM)。选取的频率范围为500～2 000 Hz，并离散为25个频带，两种方法使用的预估计DOA值都采用真实DOA值，聚焦矩阵的构造均使用RSS方法[16]。空间谱实验结果见图4，可以看出本文的方法能分辨所有源信号的DOA值，CSSM-PM方法只能勉强分辨源信号的DOA，并且存在伪峰，CSSM方法则不能分辨。其中CSSM-PM方法要求相关噪声的协方差矩阵具有Toeplitz结构，然而这一条件多数情况下也很难满足。

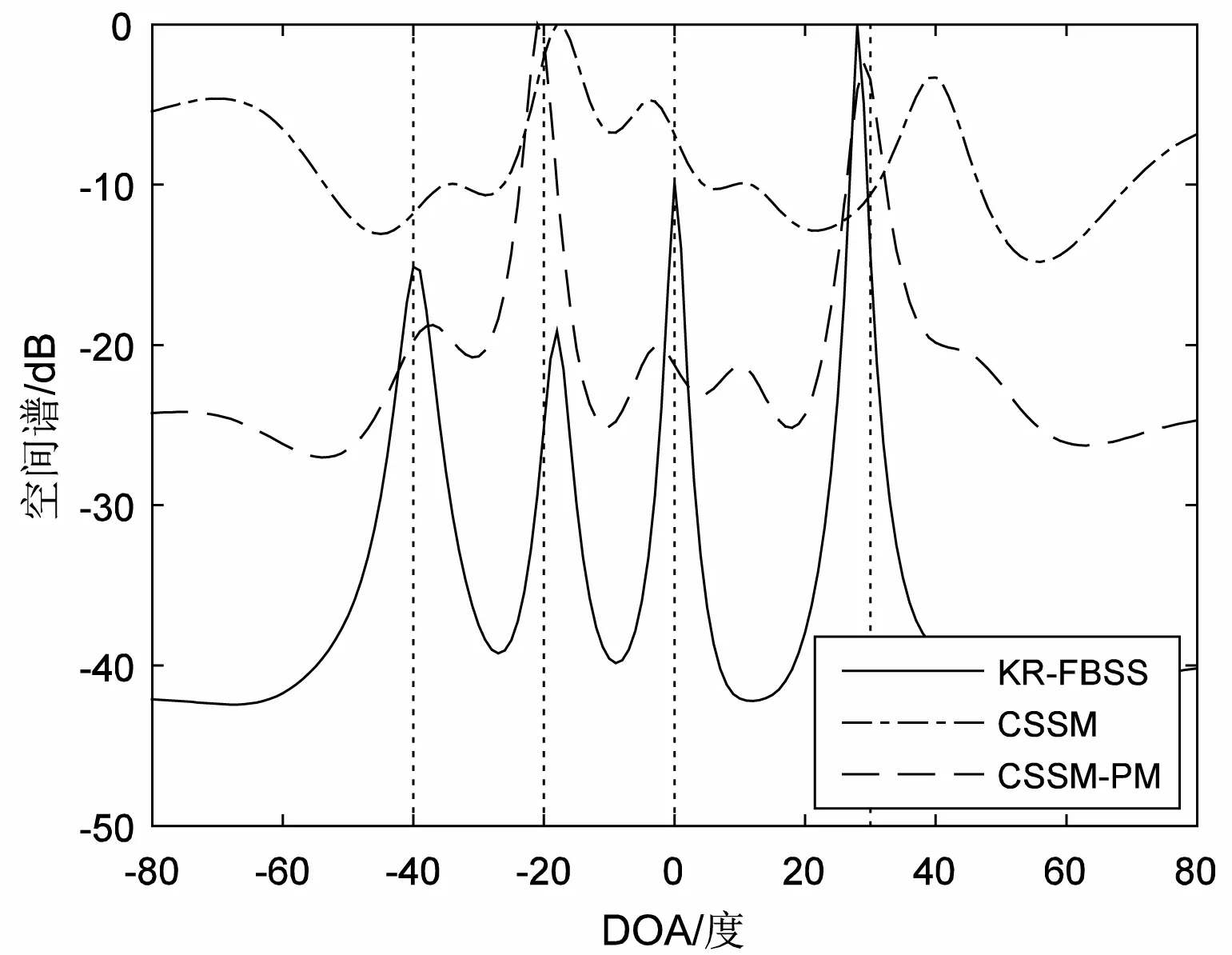
图4 宽带DOA估计空间谱

5 结 语

在准平稳信号源和相关噪声环境下，本文研究了采用Khatri-Rao(KR)子空间和前后向空间平滑理论的波达方向估计方法。与常见前后向空间平滑方法及Khatri-Rao子空间等方法相比，具有更高的检测概率和更低的均方根误差。同时，由于实际环境中的噪声可能包含部分干扰源信号，可能具有一定的相关性。本文算法通过利用KR子空间方法将各帧Toeplitz矩阵组合成新的信号模型，因此对相关噪声有较强的适应性，比常见相关算法表现更好，且在噪声相关系数变化下均有接近或较好的性能表现。此外，算法的RMSE分别随着SNR、帧长度和帧数的增加而变小，同时算法对宽带阵列信号模型也具有一定的有效性。