基于MPC的永磁同步电机最优滑模控制
郑江平 李 超
1(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105) 2(山东医学高等专科学校附属医院 山东 临沂 276000)
0 引 言
永磁同步电机PMSM具有体积小、结构简单、转动惯量较小、过载能力强等多方面的优点,现如今已被大量运用于新能源汽车、航空航天、机器人等许多工程领域。常规的PID调节方式已经远不能满足高性能的控制需求,对于交流PMSM控制系统的研究具有重要的现实意义[1-4]。
随着现代的非线性控制方法的不断发展,许多先进的控制方法已经实现PMSM的良好控制性能。然而,在调速过程中系统往往存在不确定性干扰,从而影响系统的稳定性。针对PMSM调速系统存在的不确定性干扰的扰动观测器的研究,越来越受到研究人员的关注。文献[5]提出一种针对多输入输出控制系统干扰抑制问题的非线性干扰观测器。文献[6]设计了一种基于标准扩张状态观测器的控制方法,仅适用于一类单输入单输出的系统不可或缺的链相匹配的不确定性。文献[7]针对匹配的干扰/不确定性干扰,利用适当扰动补偿增益,研究了一种新颖的复合控制方法,用来抵消“不匹配”的集总干扰的输出通道,该策略适用于非线性磁悬浮悬挂系统。减弱了这类非匹配扰动的限制,增强了非线性扰动观测器方法的适用性,但是在许多系统中,仍然会受到一定的限制。
滑模控制SMC(Sliding Mode Control)的特点在于系统进入滑动模态过程不会受到系统内部参数摄动和外部扰动的影响,且响应速度快。文献[8]将线性滑模控制运用到PMSM系统的控制中,其结构简单而且响应速度快,获得了良好的控制效果。文献[9]研究了一种基于非线性滑模面的PMSM自适应滑模控制策略,采用自适应方法进行参数校正,有效地整定控制增益参数,削弱了调速系统中的抖振现象。
本文针对PMSM调速系统存在的不确定性扰动和传统的线性滑模的控制增益较大易存在抖振现象的问题,研究了一种的基于模型预测控制(MPC)的PMSM最优滑模控制方法。以MPC控制器作为电流控制内环,结合最优控制与滑模控制各自的优势,设计最优滑模速度控制器,抑制了转速的超调量,提高了系统的启动性能。设计了扰动观测器并对系统进行前馈补偿,有效地抑制了不确定性扰动,削弱了系统的抖振现象,提高了调速系统的抗扰性能。运用李雅普诺夫理论证明了控制系统的稳定性。仿真结果验证了该方法的有效性。
1 PMSM的数学模型
以表贴式PMSM为被控电机,假定永磁体无阻尼作用且空间磁场分布为正弦分布,不计涡流与磁滞的损耗的情况下,PMSM在同步旋转d-q坐标系下的动态数学模型为:
(1)
PMSM转矩方程为:
Te=pψfiq
(2)
PMSM运动方程为:
(3)
式中:ud、uq分别表示为d、q轴的电压分量;id、iq分别表示为d、q轴的电流分量;Ld、Lq分别表示d、q轴电感;R为电机定子绕组的电阻;ω为电机的电角速度;φf为永磁体与定子交链磁链;Te为电磁转矩;J为转动惯量;TL为负载转矩;p为极对数。
2 预测电流环的设计
2.1 建立电流预测模型
考虑实际工程应用中数据处理过程要求模型离散化的思想,选择采样周期为T=0.1 ms。由式(1)电流方程离散化可得:
(4)
(5)
将式(5)简化可得电流环的预测模型为:
ΔI(k+1)=AmΔI(k)+BmΔu(k)
(6)
y(k)=CmΔI(k)+y(k-1)
(7)
由此得到模型预测方程为:
Y=LΔI(k)+ΦΔu
(8)
式中:
Y= [y(k+1|k)y(k+2|k)y(k+3|k) …
y(k+NP-1|k)]T
式中:y(k+i|k)为在控制器k时刻对k+i时刻的预测输出值;ΔU为未来的控制变量。Np为预测时域,Nc为控制时域。这里,Np=10,Nc=3。
2.2 反馈校正
由于系统存在着外部扰动和模型失配的影响,所以对电流进行反馈校正。采用电流转速误差直接对预测输出进行补偿,补偿量为实际运行电流和预测输出电流的误差。对比k-1时刻的系统变量预测值和实际值的关系,可得到其存在的预测输出误差:
ε(k)=y(k)-yP(k)
(9)
式中:yP(k)为k时刻的模型输出值。
在第k时刻,对预测误差ε(k)进行修正,得到其电流矢量的修正值为:
ym(k+1)=yP(k)+δε(k)δ∈[0,1]
(10)
式中:δ为偏差补偿参数。
2.3 滚动优化
为了获得控制系统预测电流的最优控制,消除逆变器的开关时间的限制,本文选取二次评价函数为:
JM=min{δy[(ym(k+1))-Rt(k+1)]2+
R[ΔU(k)]2}
(11)
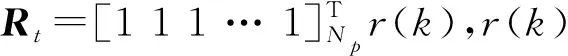
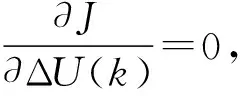
由于:
u(k)=u(k-1)+Δu(k)
(12)
最后,迭代得出最优的控制变量ud(k)、uq(k)。
3 最优滑模控制器的设计
为了提高控制系统的动态性能,结合最优控制与滑模控制各自的优势,研究了最优滑模速度控制器。
取PMSM系统的状态变量为:
(13)
由式(2)、式(3)可得:
(14)

(15)
取线性滑模面为:
s=cx1+x2
(16)
式中:c为常数且c>0。
c值大小将会影响到滑动模态的动态品质及其渐进稳定性。因此选取最优的c尤为重要。
当系统在切换面上运动时,
cx1+x2=0
(17)
因此滑动模态方程表示为:
(18)
设定系统的优化性能指标函数为:

(19)
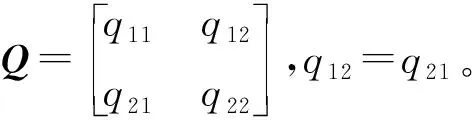
由于系统进入滑动模态运动时,滑模运动与系统控制量无关,则式(19)的末项可以忽略不计。于是:

(20)
因此,二次型整理后为:
(21)
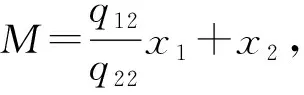
于是性能指标函数修改为:
(22)
则对应的滑动模态方程调整为:
(23)
利用二次性能指标最优控制求解法,根据李卡提方程:
(24)
可求解出P,因此推出切换函数c的值为:
(25)
为了提高控制系统的动态品质,这里选择指数趋近律,其表达式为:

(26)
式中:k>0,ε>0。
于是,可得出:
(27)
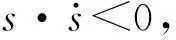
为了降低系统的不连续性,削弱系统的抖振,这里利用F(s)替换符号函数,F(s)的具体表达式为:
F(s)=2/(1+e-αs)-1
则可得到最优滑模速度控制器的控制量为:
(28)
4 扰动观测器的设计
在速度控制的过程中,若对系统的不确定扰动进行观测,进而通过观测值对系统的扰动前馈补偿,则在滑模控制中存在的不连续项将会降低,取得削弱抖振效果。
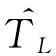
(29)
式中:g为常数。图1为扰动观测器结构框图。
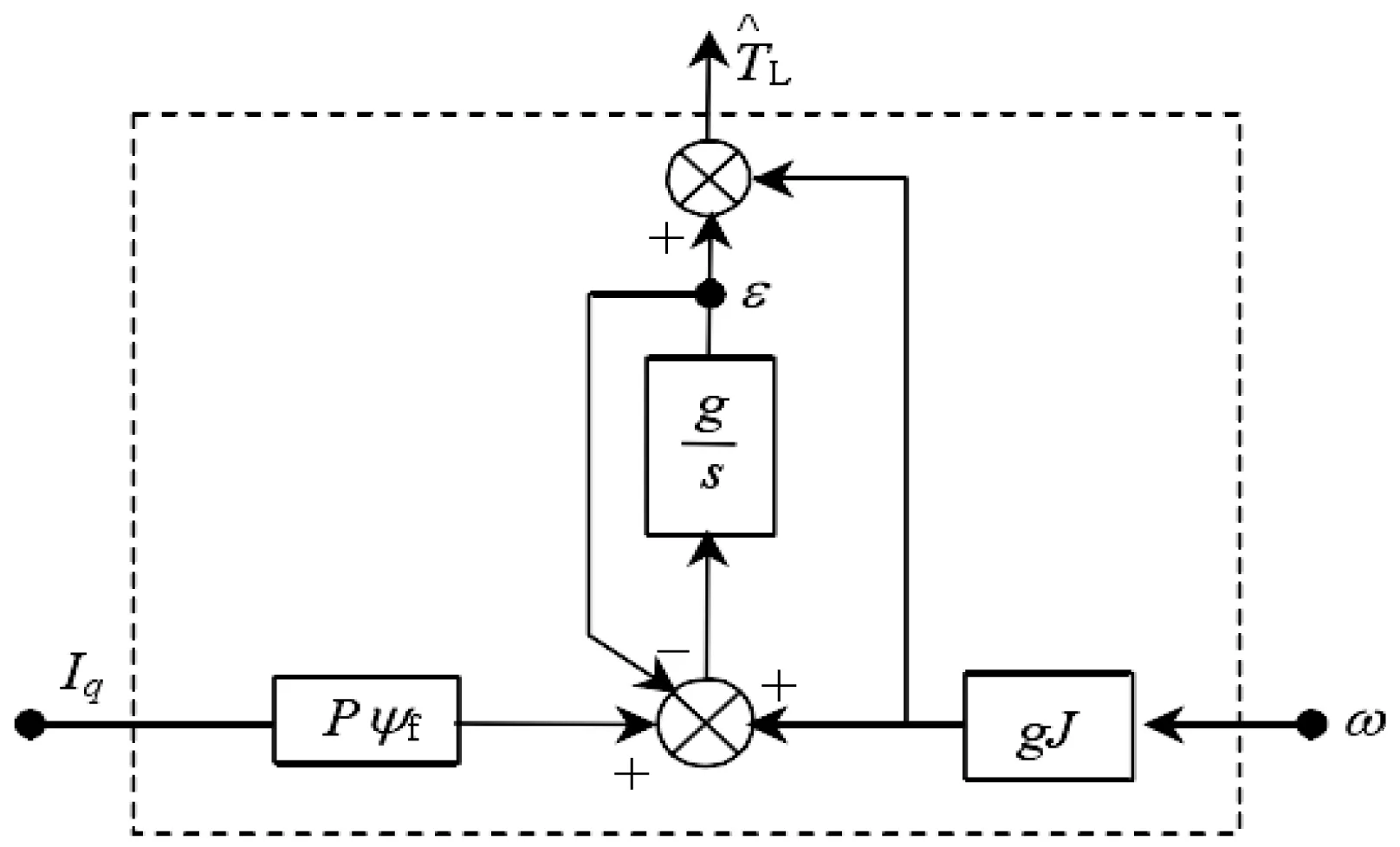
图1 扰动观测器结构框图
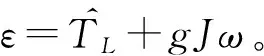
(30)
则:
(31)
求得:
ΔTL=ae-gt
(32)
式中:a为常值,观测误差ΔTL随时间递进按指数的规律趋近于0,观测器的趋近速度受g的大小影响。
于是,将扰动观测器的输出前馈至电流调节器的输入,得到最终的电流给定为:
(33)
式中:k为扰动观测器的作用系数,k>0。
5 仿真及实验验证
为了检验本文提出的策略的有效性,采用MATLAB/Simulink搭建了电机调速系统的仿真模型。选用PMSM的参数如表1所示,系统的控制框图如图2所示。
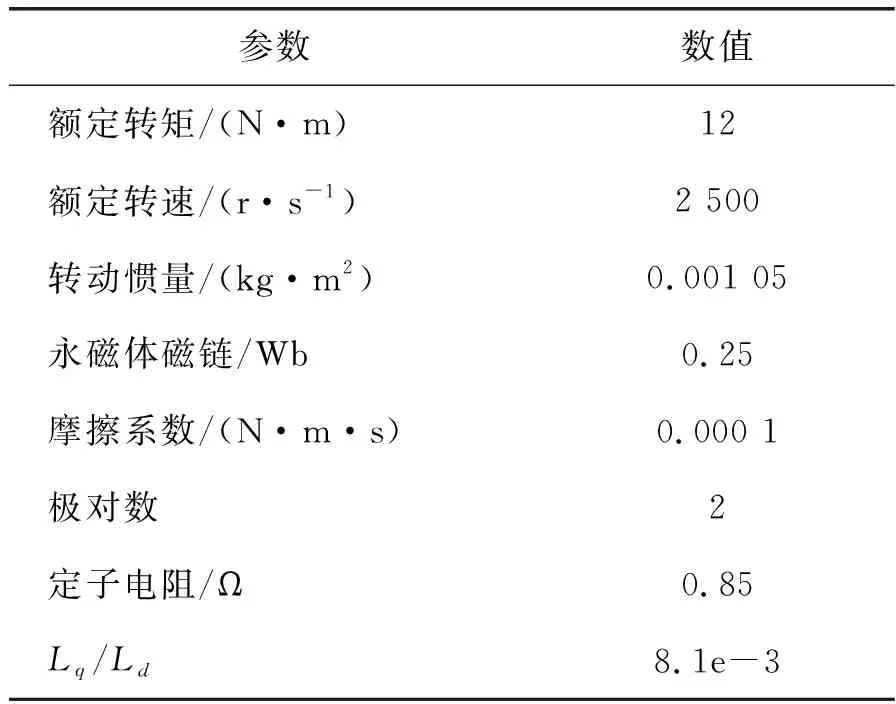
表1 永磁同步电机的主要参数
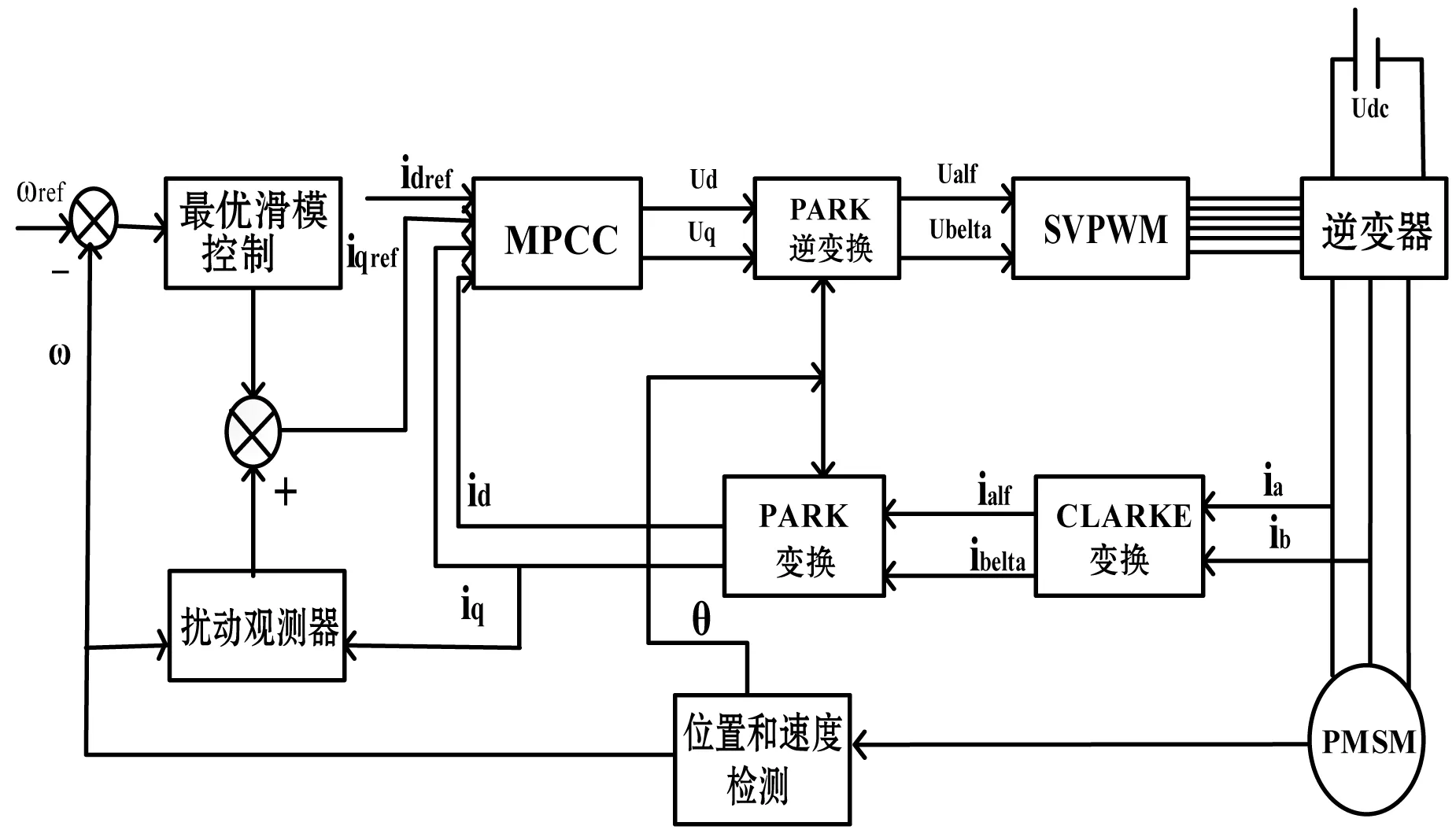
图2 PMSM调速系统的控制框图
图3为本文算法与常规的PI进行对比的转速空载响应曲线。系统初始给定转速为100 rad/s,从图中曲线可看出,基于MPC的PMSM最优滑模控制的控制方法启动平稳无超调,有效地提高了系统的启动性能。
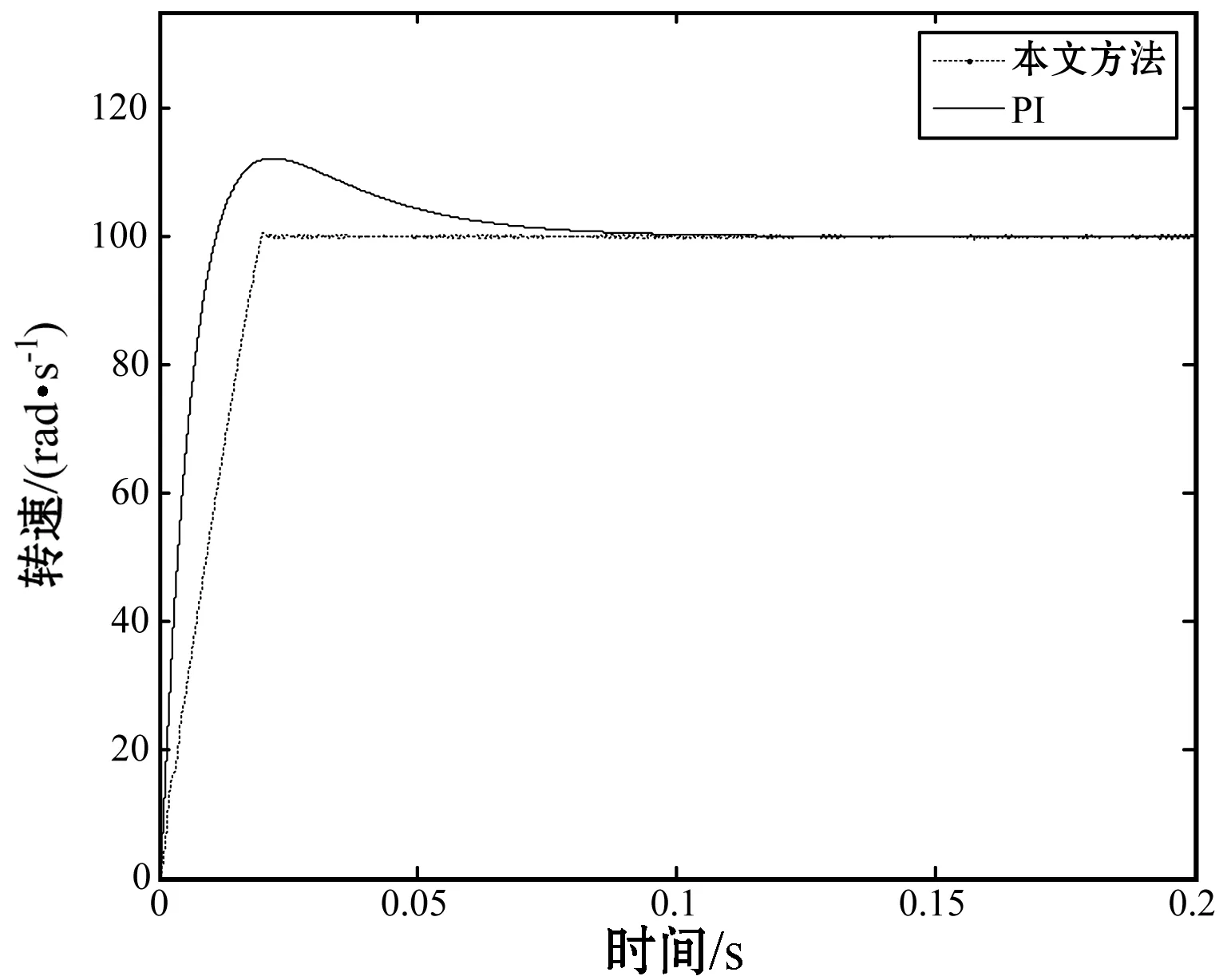
图3 空载响应曲线
图4为负载扰动时电流波形曲线。可以看出本文方法在系统受到扰动时,电流纹波较好,电流动态性能稳定。
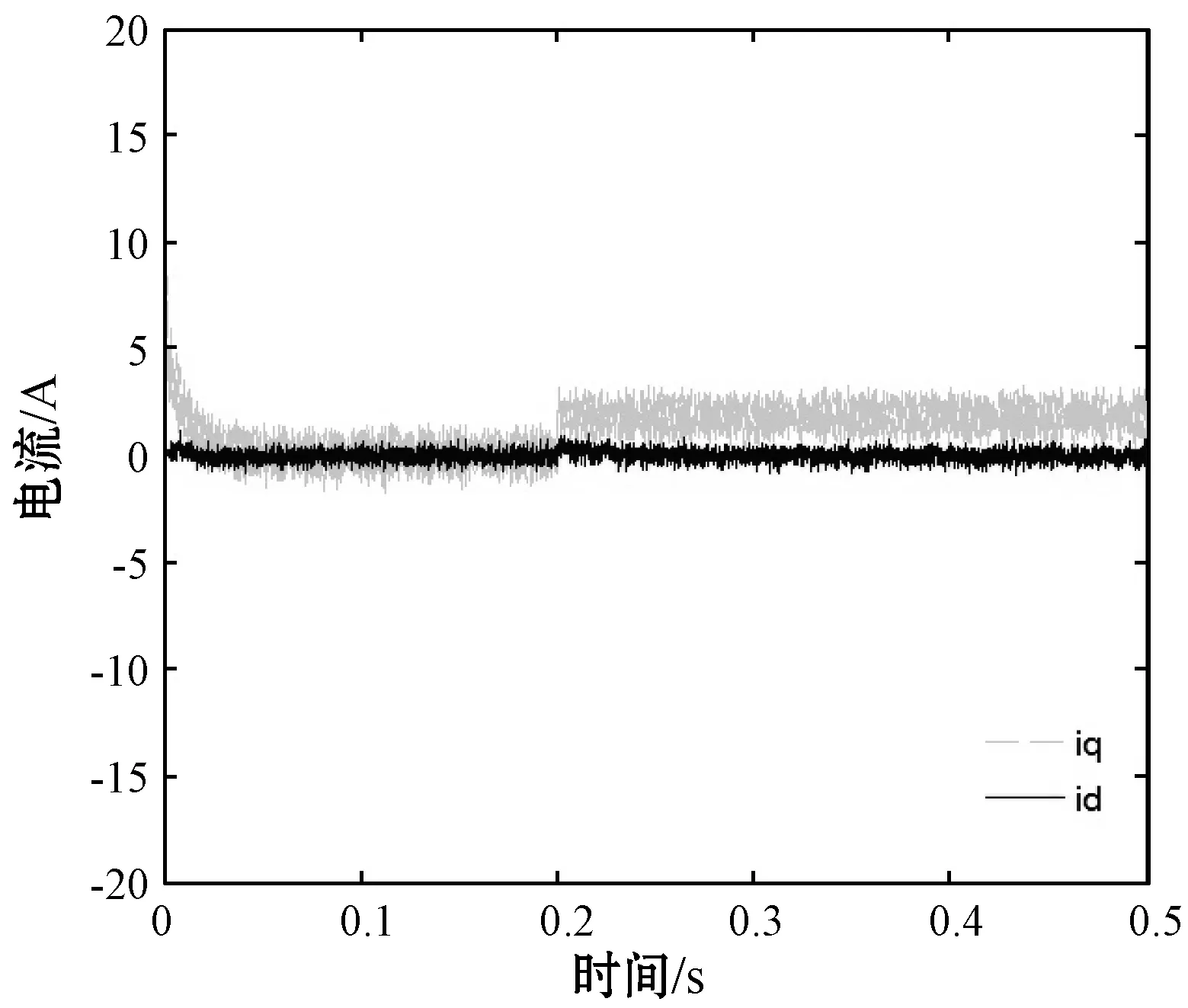
图4 受扰动时电流响应曲线
从图5的对比中可以看出,本文控制方法在系统阶跃给定时的转速响应快速且无抖动,有效地削弱了系统存在的抖振现象,实现了较好的控制效果。
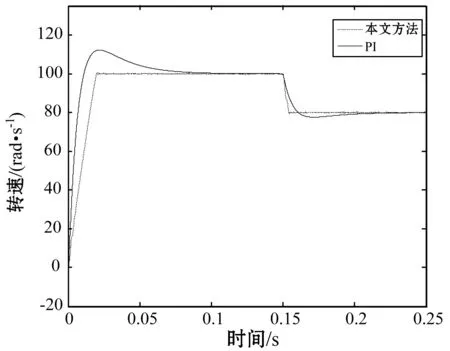
图5 阶跃给定时速度对比曲线
图6为本文控制策略与PI控制器在加载时的速度对比曲线。对比显示本文策略在系统加载过程中,转速受外部扰动时的波动较小,表现出较强的鲁棒性。
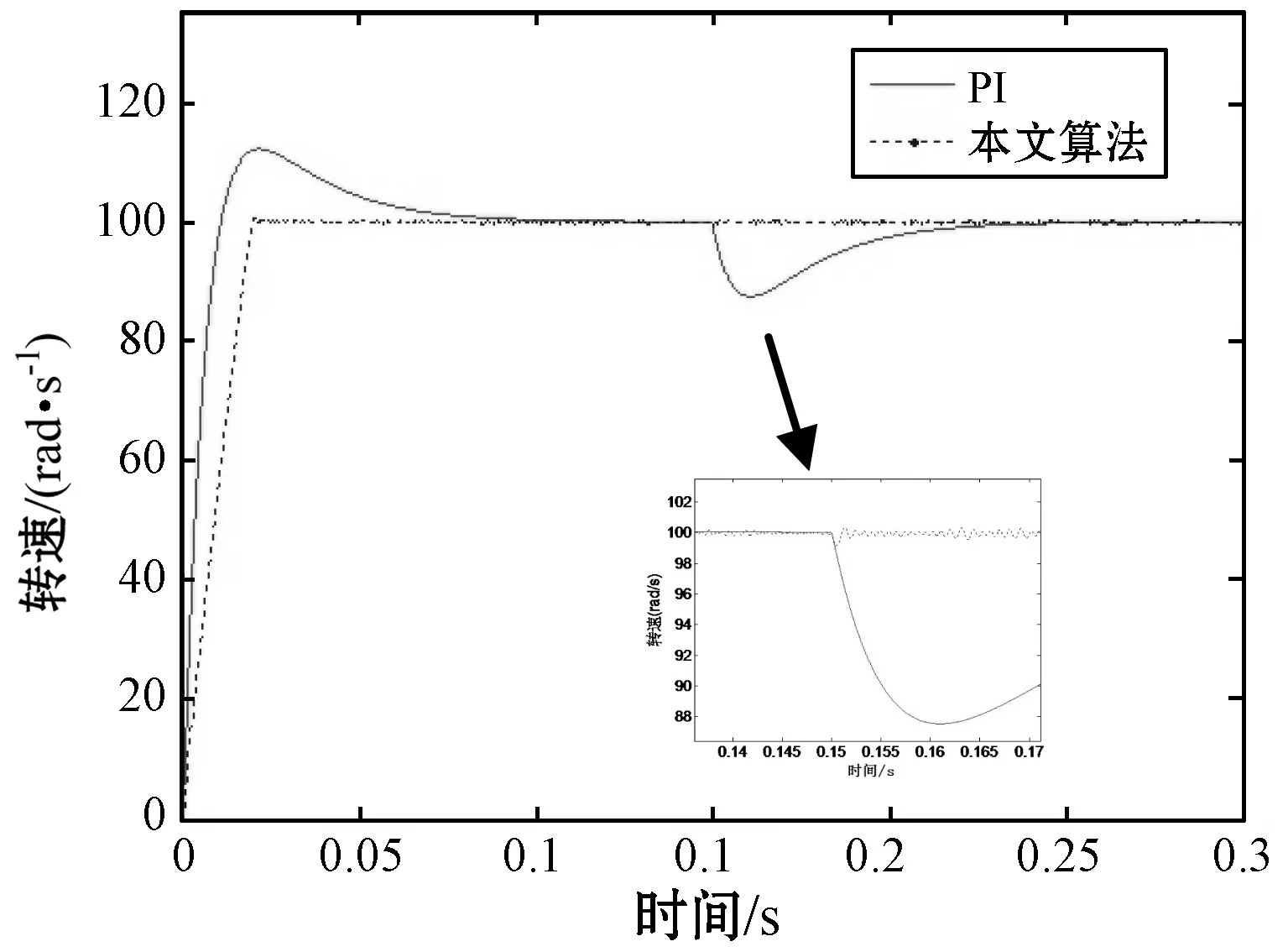
图6 加载时速度响应曲线
图7为扰动实际值与估计值对比曲线,当在t=0.2 s时,突加3 N·m的负载扰动,然后在t=0.4 s时,将转动惯量由电机J=0.000 105 1变化为0.000 205 1。由图中可以看出,扰动观测值很好地跟随了实际扰动值曲线,达到了较为理想的效果。
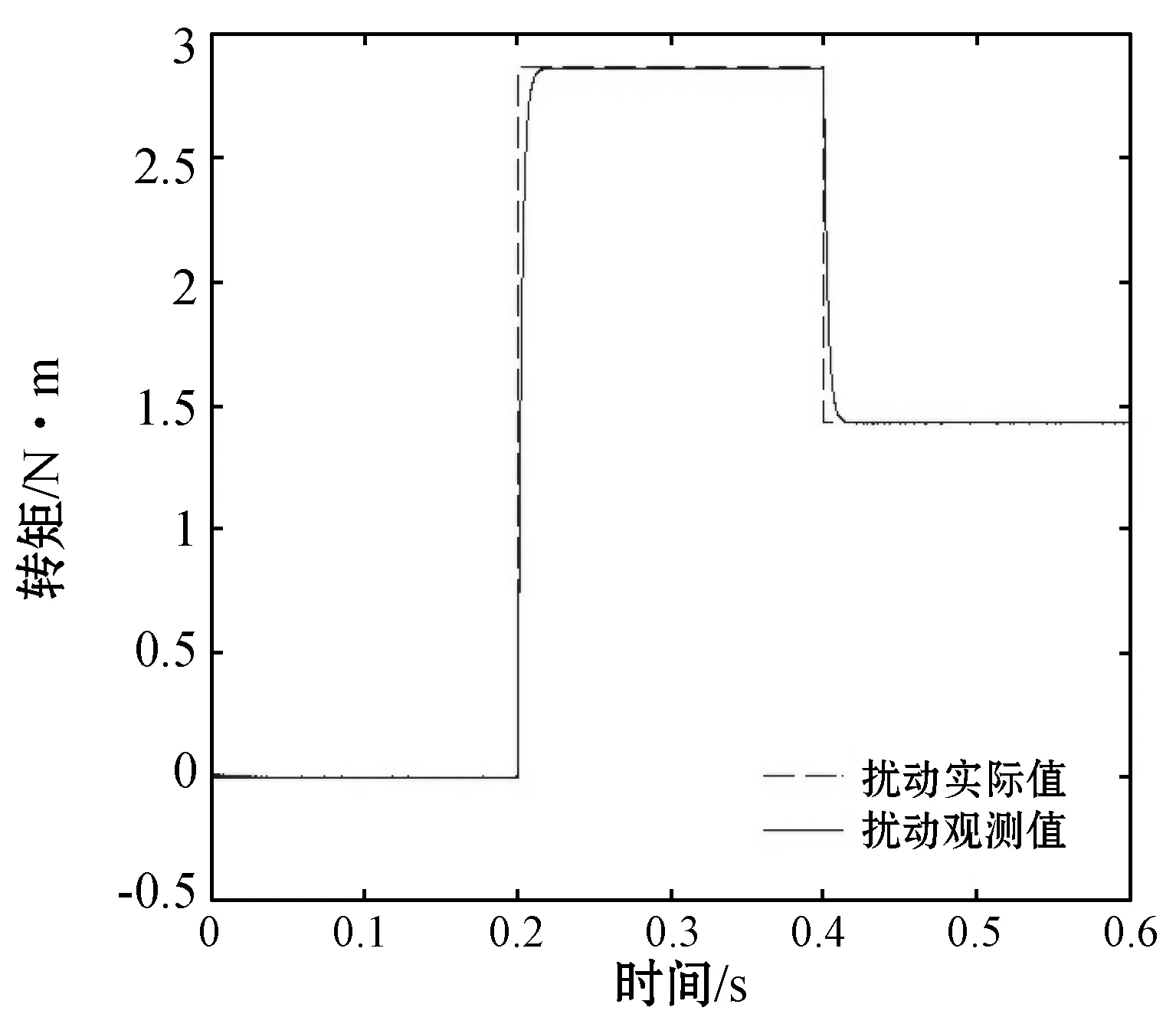
图7 扰动实际值与估计值对比曲线
6 结 语
本文研究了一种新的基于模型预测控制(MPC)的PMSM最优滑模控制策略。以模型预测电流控制作为控制内环,针对PMSM调速系统存在的不确定性干扰,设计带扰动补偿的最优滑模速度控制器,有效抑制了超调,提高了系统的启动性能,改善了调速系统的鲁棒性。并采用李雅普诺夫理论证明了控制系统的渐进稳定性。仿真结果验证了该方法的有效性。

