自适应尺度的双边纹理滤波方法

王 辉，王 悦，刘畅祖，庄珊娜，曹俊杰

(1．石家庄铁道大学信息科学与技术学院，石家庄050043; 2．大连理工大学数学科学学院，辽宁大连116024)(*通信作者电子邮箱wanghui19841109@163．com)

0 引言

结构保持的纹理平滑在计算机视觉和图形学的很多应用中起着重要的作用，例如，细节编辑、色调映射、特征边提取和图像分割等。近些年来，对结构保持的纹理平滑的研究得到了越来越多的关注［1－11］，然而，这依然还是一个比较具有挑战性的问题，因为将纹理和结构区分开很困难。

目前，大多数结构保持的纹理平滑方法利用图像上矩形片的统计量来区分纹理和结构，例如，双边纹理滤波(Bilateral Texture Filtering， BTF)［1］、相 对 全 变 分 (Relative Total Variation，RTV)［3］、相 应 图 像 特 征 的 协 方 差 (Region Covariances，RC)［4］等。由于矩形片的边长对于所有像素都是固定的，因此选择合适的矩形片边长很困难，如果边长取值比较小就不能够有效去除纹理，如图1(b)所示;相反，如果边长取值比较大，就会将一些细小的尖锐结构平滑掉，如图1(c)所示。图1(d)中本文参数为T=0．9 m，niter=5。

图1 本文方法与单尺度双边纹理滤波的比较Fig．1 Comparison between the proposed method and single-scale bilateral texture filtering

借鉴图像分割、目标跟踪和滤波等工作中自适应尺度的选取方法，本文提出了一种自适应尺度的纹理平滑方法，使得每个像素可以根据局部信息进行自适应地选取最合适的矩形片边长，这样可以在保持图像结构的同时有效去除纹理，如图1(d)。相对于以前自适应尺度的纹理滤波方法［10－11］，本文方法取得更好的结果。

1 相关工作

1．1 结构保持的纹理平滑

传统的保持特征边的图像平滑方法主要是基于颜色对比度，将对比度低的细节平滑，而保持具有高对比度的特征边。由于纹理的对比度往往比较高，从而上述方法不能够有效地去除纹理。

Subr等［2］将细节定义为给定尺度下的极值包络曲面之间的差，利用局部极值(Local Extrema，LE)可以在一定程度上去除纹理。Xu等［3］对于每个像素定义了一种称之为相对全变分的度量来区分图像中的纹理和主要结构，其中像素上的相对全变分是以该像素为中心的矩形区域中梯度的一个统计量。文献［4］中提出了一种加权平均的保持结构的纹理平滑方法，其中两个像素之间的相似性是由以像素为中心矩形片上一些特征的协方差矩阵的相似性决定的。

基于图像上最小生成树距离的滤波方法也用到保持结构的纹理平滑中［6，9］。有的结构保持的纹理平滑方法先通过高斯滤波平滑掉图像中的纹理，然后利用特定的策略来恢复出图像中的主要结构［5，7－8］。Zhang 等［7］提出旋转引导滤波(Rolling Guidance Filter，RGF)，先利用高斯滤波去除纹理，然后利用双边滤波进行边缘恢复。

上述纹理平滑方法中所用的矩形片边长对于所有像素都是固定的:若边长取值较大，图像过平滑;若取值较小，不能去除纹理。为此，本文提出一种自适应的纹理平滑方法，在纹理均匀区域采用较大的矩形片边长，结构边缘区域采用较小边长的矩形片。

1．2 自适应尺度选取

在计算机视觉和图像处理中，自适应尺度的方法已经广泛应用于图像分割和滤波等应用中［10－16］，其中比较常用的是Linderberg［12－13］提出的尺度空间方法。它先对图像进行高斯滤波，得到不同尺度的图像;然后根据尺度图像的梯度或拉普拉斯等微分量为每个像素选取最优尺度。比如，对图像进行斑点检测时，每个像素的最优尺度为具有最大归一化拉普拉斯的尺度。本文基于该方法，利用尺度图像上归一化后的梯度和拉普拉斯的线性组合来自适应地选取矩形片边长，从而进行自适应的纹理平滑。

Lin等［10］提出利用矩形片上梯度的统计量来区分纹理与主要结构，给定一个矩形边长，如果统计量小于给定阈值，则选择该边长，否则选取比给定边长小2的矩形片边长。这种从两个尺度中进行选择的自适应方法，它的结果很大程度上依赖于事先给定的边长，如果给定边长取得不合适会出现纹理未平滑或者过平滑的现象。在双边纹理滤波［1］的基础上将从x、y方向计算相对全变分改为从不同角度进行计算，然后利用标准化后的整体平滑度(Collective Fatness，CF)为每个像素选择最优的矩形片边长［11］。文献［17－18］则根据图像中噪声点选择滤波窗口的尺度，然后利用中值滤波进行滤波。本文借鉴经典的尺度空间理论［12－13］，在给定候选边长集中为每个像素自适应地选取矩形片边长，然后利用双边纹理滤波进行图像平滑，最后取得比CF更好的结果。

2 自适应尺度选取

给定一幅图像I，对图像进行自适应选择尺度前，需要先对图像进行高斯滤波［12－13］，得到尺度图像 L(x，y;σ):

其中:gσ为高斯函数，参数c为常数2．1214，Kj∈K，其中K为给定的σ候选参数集。

本文采用Linderberg［12－13］提出的尺度图像归一化的一阶导数和二阶导数的线性组合，

对于每个像素，按照K中元素的顺序，计算相应的σ与ΔLσ，如果ΔLσ小于阈值T，则选择该像素尺度为σ，纹理平滑时矩形片边长kσ=round(3σ)(若其为偶数，kσ=kσ+1)，否则，选取K中下一个元素的ΔLσ与T进行比较。本文借鉴文献［10］中降序思想对图像进行自适应选取矩形片边长，K={2．5，2，1．5，1，0，－1，－ 2}，可选取的矩形片边长集为Kp={15，13，11，9，7，5，3}，其中包含了纹理平滑时常用的矩形片边长，从而对于不同的纹理图像，可选取合适的矩形片边长，既可以保持图像的边缘结构又可以去除纹理。

本文中阈值与σ相关，在每个尺度下首先计算输入图像ΔLσ的平均值mσ，然后对所有尺度下mσ求平均值得到m。一般情况下，阈值T的取值范围为［0．5 m，1．5 m］时即可取得不错结果，对于大多数纹理图像，阈值T=0．9 m时可以取得很好的结果。

对于彩色图像，先分别计算像素p在RGB三个颜色通道上的偏导 Lx、Ly、Lxx、Lyy、Lxy，然后利用三个通道的和计算ΔLσ，进而找到合适的矩形片边长。

3 双边纹理滤波

本章简单地介绍结构保持的双边纹理滤波方法，具体细节请参见文献［1］。给定一幅灰度图像I，双边纹理滤波方法主要包含以下两个步骤:

步骤1 给定纹理图像平滑时的矩形片边长k，利用片漂移的策略生成纹理描述的图像G'用来引导步骤2中的双边滤波。对于每一个像素p，在k2个k×k的包含p的矩形片中，最能描述该像素纹理信息的矩形片Ωq具有最小的相对全变分(mRTV):

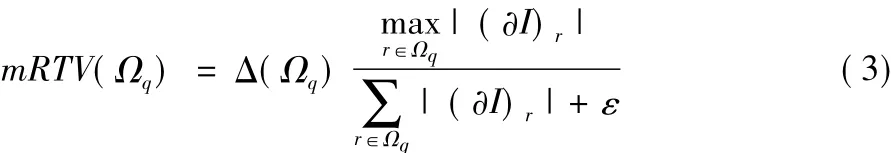
其中:Ωq是以像素q为中心的k×k的矩形片，|(I)r|=是像素r∈Ωq上梯度的模，参数ε=10－9是为了避免除数为0，Δ(Ωq)是灰度范围:

其中:Imax(Ωq)和Imin(Ωq)分别代表矩形片Ωq上像素灰度值中的最大值和最小值。

像素p上代表性的纹理矩形片Ωq选好后，引导图像G在p上的灰度值定义为Ωq上像素灰度值的平均值，记为Bq，即Gp=Bq。最后，为了避免噪声的敏感性，引导图像G'在p上的灰度值定义为Gp和Bp的线性组合:其中:，参数σ固定为5k。

步骤2 得到引导的纹理描述图像G'后，对于原始图像I上的引导的双边滤波为:

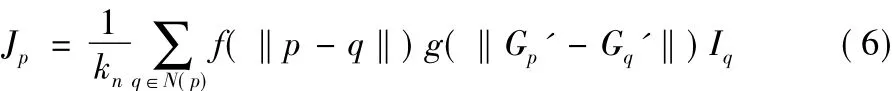
其中:kn是归一化项;N(p)是以p为中心的s×s矩形片中的相邻像素;f和g是两个高斯函数 f(x)=对应的参数分别为δs和δr。

在上述算法中，一些参数固定为s=2k－1，δs=k－1，δr=0．05sqrt(c)，其中c为引导图像中颜色通道的数目。一般来说，一幅图像需要迭代3～5次才能得到理想的结果。对于彩色图像，先对RGB三个通道上分别计算式(3)中的相对全变分，然后利用它们的和在每个通道上进行片漂移，得到一幅彩色的引导图像G'。

4 本文算法

本文提出的自适应尺度的双边纹理滤波主要分为两部分:自适应地选取矩形片的边长和进行自适应的双边纹理滤波。算法1描述了本文自适应的双边纹理滤波方法的一次迭代过程，对应的中间结果如图2所示。其中，图2(b)为自适应尺度的选取结果，其中在图像的边缘结构处选取较小的矩形片边长，在纹理区域选取较大边长，图2(c)为双边纹理滤波时的引导图像，图2(d)为第一次迭代的结果，图2(e)为最终结果。图2(e)中参数为T=0．9 m，niter=5。

首先，从 K={2．5，2，1．5，1，0，－1，－2}候选集中，为每个σ计算尺度图像归一化的一阶导数和二阶导数的线性组合ΔLσ，并与阈值进行比较，选取小于阈值的ΔLσ，从而为每个像素自适应地选取最合适的 σ，进而根据 kσ=round(3σ)选择最合适的矩形片边长，这样既可以在纹理均匀区域采用较大边长的矩形片，又可以在结构边缘区域采用较小边长的矩形片，具体方法见第2章。

然后，对每个像素及其选择的矩形片边长进行自适应的双边纹理滤波。传统的双边纹理滤波［1］中矩形片边长k对于所有的像素都是固定的，而本文方法中，矩形片边长kp是根据图像的局部信息，从相应的候选矩形片边长集中自适应地选择合适的边长，如图2(b)所示。在此基础上与传统双边纹理滤波类似，计算它们的相对全变分，利用片漂移得到引导图像，再根据式(6)中的双边纹理滤波得到最终的平滑结果。图3将本文与其他纹理平滑方法中引导图像进行比较，通过对比，可以看出本文的引导图像在去除纹理的同时能更好地保持图像的边缘结构。图3参数为CF:σ=5，BTF:k=5，niter=5，本文方法:T=0．5 m，niter=5。

图2 自适应尺度双边纹理滤波方法的中间过程Fig．2 Intermediate process of adaptive scale bilateral textture filtering method

图3 本文引导图像与其他保持结构方法引导图像的比较Fig．3 Guidance image comparison between the proposed method and other structure-preserving methods

算法1 自适应尺度的双边纹理滤波。

输入 图像I和按降序排列的候选参数集合K={2．5，2，1．5，1，0，－1，－ 2}。

输出 纹理平滑后的图像J。

通过式(1)得到L(x，y;σ)，利用式(2)得到图像归一化后的一阶导数和二阶导数的线性组合ΔLσ

if ΔLσ＜ T

kp=kσ，跳出循环

end if

end for

end for

利用kp计算引导图像在p上的像素值

以G'为引导图像对I进行引导的双边滤波，得到平滑后图像J

与原有的双边纹理滤波类似，参数δr固定为δr=0．05×sqrt(c)，其中c为引导图像中颜色通道的数目，s=round(2kaver－1)，δs=kaver－1，kaver为每个图像所用矩形片边长的平均值。本文算法需要用户选择的参数为:阈值T和迭代次数niter，一般来说，T=0．9 m，迭代3～5次可以得到比较理想的结果。

5 实验比较与应用

在实验中，采用Xu提供的图像集［3］进行测试，其中包括十字绣、涂鸦艺术图、瓷砖镶嵌艺术图等。本文所有实验均在Matlab R2012a下进行，使用中央处理器是Intel Xeon CPU E5-2620 v3的台式电脑。本文需要计算图像在每个σ下的一阶导数和二阶导数的线性组合进行自适应尺度选择，然后在自适应尺度下进行引导的双边纹理滤波，所以本文方法时间主要消耗在得到自适应的引导图像和进行双边纹理滤波，迭代一次所用时间如表1所示。

在图1和图4～6中，本文自适应尺度的双边纹理滤波方法与一些经典的保持结构的纹理平滑方法进行了比较，例如传统的双边纹理滤波(BTF)［1］、局部极值(LE)［2］、相对全变分(RTV)［3］、区域协方差(RC)［4］、旋转引导滤波(RGF)［7］、保持边缘结构的整体平滑度(CF)［11］。通过实验结果比较，可以得出本文方法在去除纹理的同时，更好地保持图像的边缘结构，图7为本文方法更多的实验结果。图4参数为RGF:δs=3，k=5，BTF:k=5，niter=5，本文方法:T=0．5 m，niter=5，图5参数为BTF:k=5，niter=3，LE:k=8，RTV:λ =0．02，δ=3，CF:σ =7，本文方法:T=0．9 m，niter=5，图6参数为BTF:k=5，niter=3，CF:σ =5，本文方法:T=0．9 m，niter=5。

表1 本文方法运行时间Tab．1 Running times of the proposed method

5．1 实验比较

双边纹理滤波 本文将传统双边纹理滤波中用于纹理分析的矩形片边长由原来的所有像素共用同一个边进行推广，使每个像素根据局部信息自适应地从候选参数中选择最合适的尺度。通过图1可以看到本文方法能够在去除纹理的同时有效地保持结构，特别是细小的尖锐的结构。原因是本文方法能够在邻近图像结构边的区域自适应地选取具有较小边长的矩形片用于纹理平滑，从而能够有效保持这些细小的尖锐特征。

其他方法 在图4，5中，本文还与其他经典的保持结构的纹理平滑方法进行了比较，从中可以看出本文方法在去除纹理的同时，有效地保持细小的尖锐结构。主要原因是这些方法大都利用以像素为中心的矩形片上的统计量来区分图像中的纹理和结构，并且所有像素共用同一个矩形片边长。这些单尺度的方法为了有效去除纹理，往往把矩形片取得比较大，从而模糊了一些细小的尖锐结构。

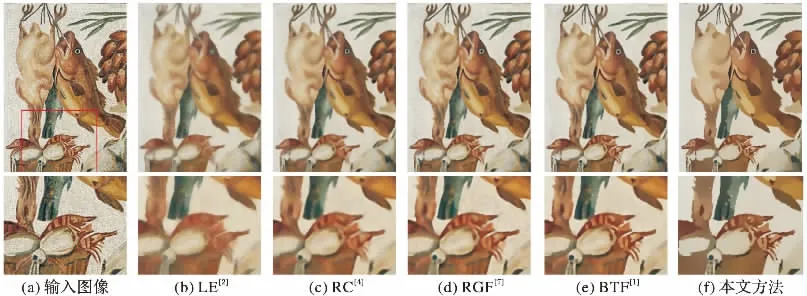
图4 本文方法与单尺度结构保持纹理平滑方法的比较Fig．4 Comparison between the proposed method and single-scale structure-preserving methods

图5 本文方法与经典的结构保持纹理平滑方法的比较Fig．5 Comparison between the proposed method and classical structure-preserving texture smoothing methods

在图5和6中，通过将本文方法与自适应尺度的CF［11］比较，可以看出本文方法效果更好，原因是CF［11］进行尺度选择时，每个像素的尺度与初始尺度相关，当初始尺度较大时，边缘处尺度较大，图像边缘处模糊;反之，初始尺度较小时，纹理均匀区域矩形片尺度也较小，纹理不能有效去除。

5．2 应用

将纹理图像进行自适应平滑后，可以将平滑后的图像应用在许多方面，比如纹理增强、边缘检测等。

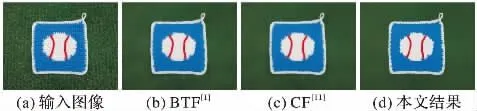
图6 本文方法与BTF和CF方法的比较Fig．6 Comparison between the proposed method，BTF and CF methods

图7 本文方法的更多的实验结果Fig．7 More results of the proposed method

5．2．1 纹理增强

纹理增强可以产生更加清楚的图像细节，获得更好的视觉效果，如图8所示。输入图像I，经过平滑后得到图像J，对纹理图像进行纹理增强，得到图像

其中，λ控制纹理增强的尺度。图8(d)中，λ=2，即对原图纹理增强2倍，从而可以清楚地看出原图的纹理组成。图8(b)参数为 T=0．8 m，niter=5。

图8 纹理增强Fig．8 Texture enhancement

5．2．2 边缘检测

对纹理图像进行Canny边缘检测时会产生很多噪声，但对平滑后图像进行边缘检测时，由于纹理去除，可以得到理想的结果。如图9所示，对纹理图像进行边缘检测时，图像中枯草和两旁的泥土被检测出来，误以为是边界，如图9(c)所示。运用本文方法进行纹理平滑后再检测边缘，图像中大量的伪边缘被去除，图像的主要结构得到有效检测，结果如图9(d)所示。图9(b)中参数为T=1．5 m，niter=7。

图9 纹理图像边缘检测Fig．9 Edge detection of texture image

6 结语

结构保持的纹理平滑方法的关键是找到一个合适的度量来区分纹理和图像结构，目前大多数方法是利用矩形片上像素的统计量区分纹理和图像的结构，然而矩形片的边长对于所有像素都是固定的，为了能够有效地去除纹理，一般选取一个较大的边长，在此过程中往往会模糊掉小于给定尺度的细小的尖锐特征。本文提出一种自适应尺度的方法，通过对每个像素的局部信息进行统计分析，从候选矩形片参数中自适应地选择最合适的边长，然后进行自适应的双边纹理滤波。实验结果表明，本文方法可以取得不错的效果。