磁性槽楔对笼型感应电机电磁参数及性能的影响

谢颖 武鑫 李飞

摘 要：电机中定子槽嵌入的槽楔由普通的绝缘树脂材料改为磁性槽楔后，电机的电磁性能有一定改变，以一台笼型感应电机为例，对同一电机分别采用普通绝缘槽楔与磁性槽楔进行了磁场、气隙系数、槽漏抗的计算并对比分析。以瞬态磁场为基础，深入分析了磁性槽楔对电机中损耗、转矩、电磁力和电磁振动等性能的影响，并对磁性槽楔在磁场中的受力进行了分析。计算结果表明，磁性槽楔可以有效的改善气隙磁密的分布，降低损耗、电磁力和电磁振动。但同时其导磁性能越高，电机的最大转矩和启动转矩也越小，而且磁性槽楔所受到的磁拉力也就越大，更容易受损，所以要综合各方面因素，选择合适磁导率的磁性槽楔。

关键词：

感应电机；磁性槽楔；气隙磁场；电磁参数；电机性能

DOI：10.15938/j.jhust.2018.03.018

中图分类号： TM343

文献标志码： A

文章编号： 1007-2683（2018）03-0104-07

The Effects on the Electromagnetic Parameters and Performance

by Magnetic Slot Wedge in a Squirrel-cage Induction Motor

XIE Ying， WU Xin， LI Fei

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：Replacing the common insulation slot wedges with magnetic slot wedges in the stator slots can change the electromagnetic performance of motor， so the magnetic field， air-gap coefficient and slot leakage reactance in a squirrel-cage which using common slot wedges and magnetic slot wedges were calculated accurately and compared in this paper. Based on the results of transient magnetic fields， the influences of magnetic slot wedge on surface loss、iron loss、torque、electromagnetic force and vibration were analyzed in depth. Meanwhile， the forces suffered on magnetic slot wedges were also be researched. The results show that the magnetic slot wedge can improve the distribution of air-gap flux density effectively and then reduce the losses、electromagnetic forces and vibration. But the higher relatively permeability it is， the maximum and starting torque of the motor are smaller and the forces suffered on magnetic slot wedge are greater， and the magnetic slot wedges are more easier to be damaged， so when to choose the suitable relatively permeability of magnetic slot wedge， comprehensive factors should be taken into account.

Keywords：induction motor； magnetic slot wedge； air-gap magnetic field； electromagnetic parameters； motor performance

0 引 言

目前高效節能已成为人们关注的焦点，而电机作为工业用电的主要电气设备之一，提高其工作效率能够大力缓解能源浪费和经济损失。一种简单、经济有效的提高电机效率的方法就是采用磁性槽楔代替普通的绝缘槽楔。由于磁性槽楔的相对磁导率高、导磁性能好，它能够有效的缓解由于齿槽结构引起的气隙磁密分布不均匀的现象，进而削弱气隙磁场中的谐波含量，减小损耗、降低电机的温升，减小振动和噪声，延长电机的工作寿命，提高工作效率[1-5]。国内外许多学者在磁性槽楔优化电机的性能方面做了很多研究，例如在文[6]中，作者研究了自制的铁粉层压磁楔对电机性能的影响，发现虽然电机的启动转矩和最大转矩减小，但电机温升降低，电机效率得到提高。还有学者研究发现磁性槽楔可以减小气隙磁阻的变化，削弱磁阻转矩，进而减小转矩脉动，同时磁性槽楔也起到了减小永磁体漏磁的作用[7]。有学者对采用不同材料和工艺的磁性槽楔进行了对比分析，发现使用粒径较小且均匀的磁粉能够改善其力学性能，用热固性树脂包覆磁粉颗粒，可提高磁性槽楔的电磁性能，模压磁楔具有较高的密度和磁性能，层压磁楔具有优异的力学性能[8-10]。文[11]作者研究了磁性槽楔在改善电动机性能上的作用及其在高压电动机中的应用，并分析了应用磁性槽楔时的注意事项。还有学者对电机采用磁性槽楔降低绕组温升做了相关实验，从实验测量结果中发现磁性槽楔对于降低温升有很好的效果[12]。

本文利用有限元法对电机采用普通槽楔与磁性槽楔分别进行瞬态磁场计算，对比分析了采用磁性槽楔前后，电机的气隙磁密、漏抗等电磁参数及损耗、启动性能、电磁力和电磁振动等性能参数的变化规律，同时对电机运行过程中，磁性槽楔的受力情况进行了分析，给出了磁性槽楔对笼型感应电机的性能影响。

1 电机模型及磁场计算分析

1.1 电机参数及假设条件

样机为一台具有转子斜槽结构的Y80M2-2笼型感应电机，其主要参数为：额定功率1.1kW，额定电压380V，定子18槽，转子16槽，转子斜槽角度20°，气隙长度0.3mm，铁心长度80mm。

本文设置槽楔材料属性分别为普通绝缘槽楔和相对磁导率为5和8的磁性槽楔。电机有限元模型如图1所示，对模型及槽楔材料做如下处理：忽略铁心产生的涡流，忽略磁饱和对磁性槽楔相对磁导率的影响，认为其相对磁导率为常数[13]，在额定工况运行条件下，对配有普通槽楔与磁性槽楔的电机进行瞬态磁场计算。

1.2 气隙磁场计算分析

电机使用磁性槽楔后，由于磁性槽楔良好的导磁性能，减小了槽口处的磁阻，有一部分磁通会流经磁性槽楔然后在经过气隙到达转子，缓解了由于齿槽效应带来的气隙磁密分布不均匀的现象，降低了气隙磁场中的谐波分量，进而有效减小谐波含量产生的损耗、振动和噪声。

提取电机运行中一个时刻的气隙磁密，对比三种情况下气隙磁场的变化规律，如图2所示。图3为对气隙磁密谐波分析得到的各次谐波幅值。

从图2和图3可知，磁性槽楔能够较好的减小气隙磁密波形波动，削弱畸变程度，各次谐波含量在一定程度上的都有所减小。而且随着相对磁导率的提高，畸变程度减小的越来越明显。

2 磁性槽楔对电机参数的影响

2.1 气隙系数的计算分析

气隙系数kδ是电机设计中的一个重要参数，表征了由于齿槽的结构存在而使气隙增大的倍数。采用普通槽楔和磁性槽楔的气隙系数计算公式分别为[14]：

Kδ=t1（t1-bt）+4πδln（1+πbt4δ）（1）

Kδμk=εt1（t1-bt）+4πμkδln（1+πbt4μkδ）（2）

ε=t1+10δKδ[（t1-bt）+10δ]（3）

式中t1为定子齿距；bt为定子齿宽；ε为修正系数；δ为气隙长度；μk为磁性槽楔相对磁导率。结合上式对电机采用普通绝缘槽楔和磁性槽楔进行计算，得到对应的气隙系数变化趋势，如图4所示。

普通槽楔时气隙系数kδ=1.733，电机采用相对磁导率为5和8的磁性槽楔后，其气隙系数分别为kδμk5=1.552和kδμk8=1.482，仅为原气隙系数的89.545%和85.52%。可见，随着磁性槽楔磁导率的增加，电机的气隙系数越来越小。这也说明了气隙系数的减小相当于缩短了气隙的有效长度。

2.2 采用磁性槽楔后电机漏抗的变化

使用磁性槽楔会改变主磁通的分布，进入槽楔的磁通量较采用普通槽楔时增多，改变了定子槽漏抗的大小，定子槽漏抗的计算公式如式（4）所示：

Xs=2πfN2μ0l[h23b1+μkh1b1]（4）

式中：b1为槽口宽度；h1為槽口高度；h2为定子槽高；l为铁心长；N为导体数；μ0为真空磁导率。

在电机使用磁性槽楔后，μk为恒大于1的常数，其他参数固定不变。经过计算得到普通槽楔及磁性槽楔的定子槽漏抗如图5所示。

由图5可以看出，定子槽漏抗是随着槽楔相对磁导率的增加而增大，而定子槽漏抗的变化也间接的影响着电机的性能。

3 采用磁性槽楔对电机性能的影响

3.1 磁性槽楔对最大转矩的影响

电机使用磁性槽楔后，电机的最大转矩有一定程度的改变[15]，最大转矩公式如下：

Tmax=m1ΩsU212c[R1+R21+（X1σ+cX′2σ）2]，

c=（1+X1σXm）（5）

式中：U1为电源电压；m1为电机的相数；Ωs同步角速度；R1为定子绕组相电阻；X1σ为定子相绕组漏抗；X′2σ为归算后得到的转子相绕组漏抗；Xm为激磁电抗。

根据式（5）计算得出，普通槽楔时电机的最大转矩Tmax=10.56N·m，最大转矩倍数为2.85；磁性槽楔μk=5时，Tmax=10.16N·m，最大转矩倍数为2.738；磁性槽楔μk=8时，Tmax=9.88N·m，最大转矩倍数为2.577，随着槽楔相对磁导率的提高，电机的最大转矩也随着减小。

3.2 磁性槽楔对电机的启动性能的影响

电机在接通电流启动的瞬间转差率s=1，启动转矩和启动电流公式可表示为如下：

Tst=m1ΩsU21R′2（R1+cR′2）2+（X1σ+cX′2σ）2（6）

Ist=U1Xm+U1（R1+cR′2）2+（X1σ+cX′2σ）2（7）

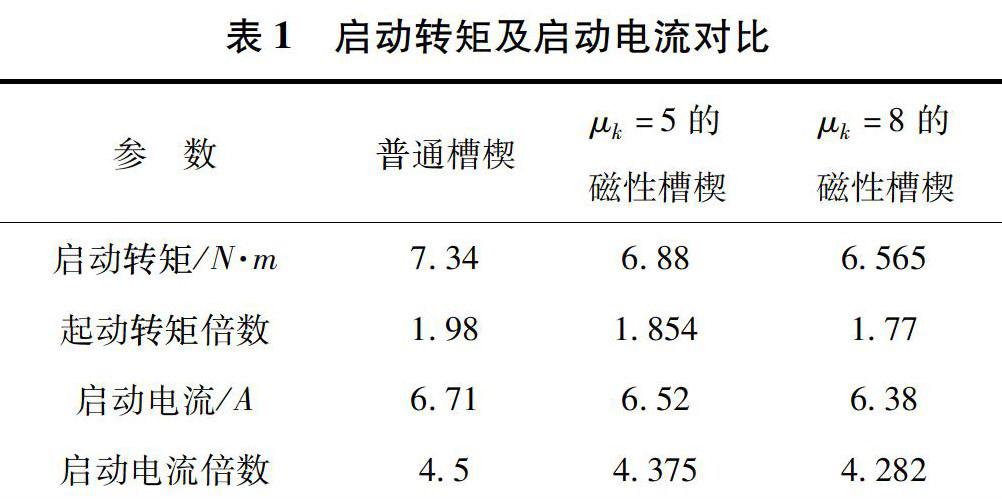
式中：R′2为归算后得到的转子相电阻，经过计算得到启动转矩和启动电流数据如表2所示。

从表中数据可以看出，采用磁性槽楔后，电机的启动转矩及启动电流都降低，并且随着磁性槽楔相对磁导率的提高，其降低的趋势也愈加明显，这对于转矩裕量较小的电机有很大的影响，因此要结合实际情况使用合适磁导率的磁性槽楔。

3.3 磁性槽楔对损耗的影响

3.3.1 表面损耗的变化

在电机运行过程中，由于齿槽结构存在，气隙磁场中的谐波分量会在定子与转子表面感生出涡流，形成了表面损耗[16]，定转子开槽在定转子表面形成的表面损耗计算公式为：

P01=0.5K0（Z2n）1.5（B01t2）2πD1l′t1t1-b01t1（8）

P02=0.5K0（Z1n）1.5（B01t1）2πD2l′t2t2-b02t2（9）

式中：P01、P02为定子表面损耗和转子表面损耗；t1、b01、t2、b02分别为定转子的齿距和槽口宽；D1、lt1、D2、lt2分别为定转子铁心外径和长度；B01为定子齿谐波磁密幅值，由有限元计算所得气隙磁密谐波分解求得；K0为经验参数，对于加工后的硅钢片来说，一般取3-5，本文取为4。不同相对磁导率的槽楔所对应的表面损耗变化如表2所示。

由上表分析得出：当磁性槽楔相对磁导率增大时，表面损耗呈现下降的趋势，而且效果比较明显。这也是由于采用磁性磁楔后，气隙系数减小，氣隙磁场分布得到了改善，削弱了气隙磁场中的齿谐波含量，进而减小了电机的表面损耗，提高了电机的输出功率，电机的效率也得以提升。

3.3.2 磁性槽楔降低铁耗的效果

基于Bertotti铁耗分离公式，可以计算得到单位体积内铁心中所产生的铁耗。Bertotti铁耗分离公式如下所示：

d（Pfe）=kfkhB2mf+σd212dBdt（t）2+kedBdt（t）1.5（10）

式中：kf为叠片系数；kh为磁滞损耗系数；σ为材料电导率；d为叠片厚度；f为电频率；Bm为单元中磁密幅值；ke为附加损耗系数。

本文中为了对比采用磁性槽楔前后定转子的铁耗分布，计算普通槽楔与相对磁导率为5和8的磁性槽楔情况下的瞬态磁场，在t=1s时刻其相应的铁耗密度分布如图6所示。三种槽楔情况下铁耗随时间变化的曲线如图7所示。

在图6中可以看出采用磁性槽楔后定转子铁耗密度分布降低许多，铁耗减小。从图7铁耗随时间变化曲线中可以看出，采用磁性槽楔后，铁耗值明显减小，而且随着磁导率的增大，铁耗减小的越多。

3.4 对电磁力及电磁振动的影响

电机运行过程中，气隙磁场产生电磁力，作用于定转子铁心，产生电磁振动，引起电机振动的主要分量是径向电磁力。分析电磁力及振动的产生原因，能够有效的采取措施削弱电磁振动问题。本文对普通槽楔和相对磁导率为5的磁性槽楔进行电磁力和电磁振动计算分析。

为了简便计算，略去振动阶数高、幅值小的力波分量[17]，由麦克斯韦定律，作用在定子铁心上的电磁力密度可表示为：

pn（θ，t）=b2（θ，t）2μ0=12μ0B212cos（2pθ-2ω1t-2φ0r）+

∑νz∑μzBνzBμz·cos[（μ±ν）θ-（ωμ±ω1）t-（φμr±φνr）]（11）

式中：b（

SymbolqA@

Symbol`@@，

Symbol`@@t）为径向气隙磁密瞬时值；v、

SymbolmA@

Symbol`@@分别为定、转子谐波次数；vz、

SymbolmA@

Symbol`@@z分别为定、转子齿谐波次数[18]。

基于瞬态磁场结果计算得到的气隙磁密，结合式（11）计算了电磁力[19]，提取同一位置的径向电磁力波时域变化曲线，如图8所示。

由图8可以看出，在电机稳定运行中，采用磁性槽楔后电磁力幅值较采用普通槽楔时小，而且波动也较小。

在电机实际运行中，四个地脚是固定不动的，所以在电磁振动计算中，设置四个地脚为零位移的约束状态。将计算得到的电磁力作为激励源，采用按时间循环加载的方式加载到定子齿表面上，在额定工况下进行瞬态动力学计算。在图9中，提取两种槽楔情况下A点的Y方向径向振动位移时域曲线，如图10所示。

由上图看出，采用磁性槽楔后，径向的振动幅值较普通槽楔减小，而且波动也减小许多，这是因为磁性槽楔改善了气隙磁场的分布，有效的降低了径向电磁力波，减小了振动。

3.5 磁性槽楔的受力分析

在电机安全运行中，磁性槽楔会受到齿区磁场对其产生的一种破坏力—磁拉力，它是槽楔磁导率μk大于1的固有特性。分析槽楔的受力情况，有助于分析槽楔损坏的根本原因，可以有效避免磁性槽楔的损坏，延长其使用寿命。

将磁性槽楔表面作为不同导磁率介质的分界面，在分界面上将会产生由导磁率较高介质指向导磁率较低介质的磁拉力[20]，如图11所示。

假设槽内没有磁通流过，磁拉力Fy= 0。由于流经槽楔的漏磁通很小，对其引起的磁拉力Fx1和Fx2忽略不计。所以现在只考虑由于磁场基波作用在磁性槽楔上产生的指向气隙的磁拉力F。拉力F随时间的变化函数为：

Fm=B2δ（μk-12μ0μk）bsin2ωt=12B2δ（μk-12μ0μk）b（1-cos2ωt）（12）

式中：b为槽口宽度；Bδ为气隙磁密；μ0为空气磁导率；μk为磁性槽楔的相对磁导率；ω为电源角频率。相对磁导率为5和8两种情况的磁性槽楔所受的磁拉力变化曲线如图12所示。

从曲线中可以看出，作用在磁性槽楔上的磁拉力F是在一个周期内以两倍工频的规律进行脉振变化的拉力，并且随着时间的变化，拉力 F变化的幅度也非常的大。在相对磁导率为5时，磁拉力的最大值为341.1N/m，而在相对磁导率为8时，其最大值为365.159N/m，这说明随着磁性槽楔导磁性能的增加，其承受的磁拉力也就越大。

4 结 论

本文对同一电机分别采用普通槽楔与磁性槽楔两种情况进行磁场、气隙系数等电磁参数计算及转矩、损耗、电磁力和电磁振动的电机性能研究，得到的结论如下：

1）仿真分析结果表明，磁性槽楔能够使气隙中的磁密分布更加均匀，降低谐波含量，减小气隙系数，因此磁性槽楔可以有效的改善电机性能。

2）电机使用磁性槽楔后，增加了定子漏抗，导致最大转矩、启动转矩和启动电流均减小，而且磁性槽楔在齿区磁场中所受到的磁拉力也随着磁导率的增加而增大，所以对于转矩裕量较小的电机，选择磁性槽楔时，要结合实际情况综合考虑。

3）使用磁性槽楔能够减小电机的表面损耗、脉振损耗和铁耗，可以有效的降低电机温升，提高电机的输出功率和效率，延长电机的使用寿命。

4）采用磁性槽楔后，电磁力波时域波形幅值减小、波动平稳，振动位移波动减小、幅值降低，磁性槽楔能够有效的抑制电机的振动。

参 考 文 献：

[1] 伍庆体.磁性槽楔的研究和应用[J].电机技术，2005（2）：49-51.

[2] 黄鹏程.磁性槽楔降低电机温升的探讨[J].电机技术，2008（3）：16-18.

[3] Kaga A， Anazawa Y， Akagami H. The Efficiency Improvement of Capacitor Motor with Ferrite Magnetic Wedges[J]. IEEE Transactions on Magnetics， 1986， 22（5）：964-966.

[4] Watanabe M， Ide K， Takahashi M， et al. Magnetically Anisotropic Slot Wedges for Rotating Machines[J]. IEEE Transactions on Magnetics，1990，26（2）：407-410.

[5] 孟大偉，刘慧敏，冯守智，等. 发电机用磁性槽楔对电磁参数与性能的影响[J]. 防爆电机，2014，49（3）：1-5.

[6] 李军，刘颖，许自贵，等. 层压磁性槽楔的性能及其对电机性能的影响[J]. 中国电机工程学报，2005，25（16）：126-131.

[7] 张海军，张京军.采用磁性槽楔改善无刷直流电机的气隙磁场[J].华北电力大学学报，2007，34（3）：17-21.

[8] 刘铁梁，陈雷. 电机用磁性槽楔的性能比较与分析[J]. 磁性材料及器件，2011，42（5）： 70-73.

[9] 李军，张龙凤，刘颖，等. 电机节能材料—磁性槽楔[J]. 材料导报，2006，20（7）：71-75.

[10]彭平，岳赟，郑晓泉.磁性槽楔研究进展综述[J].绝缘材料，2013，46（3）：37-40.

[11]顾德军，顾卫东.磁性槽楔在Y2系列高压电动机中的应用[J].电机与控制应用，2009，36（8）：63-65.

[12]姜红.采用磁性槽楔降低电机温升[J].电机技术，2005，4：55-58.

[13]汤蕴璆，梁艳萍.电机电磁场的分析与计算[M].北京：机械工业出版社，2010：304-308.

[14]李军丽，胡春雷. 磁性槽楔在电机节能技术中的应用[J]. 电机与控制应用，2005，32（2）： 57-59.

[15]汤蕴璆，罗应立，梁艳萍.电机学[M].北京：机械工业出版社，2008：175-192.

[16]梁艳萍，陈晶，刘金鹏. 磁性槽楔对高压感应电动机电磁参数和性能的影响[J]. 电机与控制学报，2010，14（3）： 1-5.

[17]代颖，崔淑梅，张千帆. 车用异步电机的电磁振动/噪声分析[J]. 中国电机工程学报，2012，32（33）： 89-97.

[18]陈永校. 电机噪声的分析和控制[M]. 杭州：浙江大学出版社，1987： 78-82.

[19]杨浩东，陈阳生. 分数槽永磁同步电机电磁振动的分析与抑制[J]. 中国电机工程学报，2011，31（24）： 83-88.

[20]王绍禹. 磁性槽楔交流电机[M]. 北京： 水利电力出版社，1987： 24-28.