青连高铁K104+080路基工后沉降预测
冯上朝,刘莎
(陕西铁路工程职业技术学院 测绘工程系,陕西 渭南 714000)
0 引言
作为一种线性工程,高速铁路穿越不同的自然地理、地质单元,岩土类型及物理力学参数的复杂性使路基极易产生工后沉降[1].对路基工后沉降进行预测并在沉降超过一定阈值时分级预警可为高铁安全运行提供信息保障[2].目前,高铁路基工后沉降预测一般采用3种方法,即基于经典土力学的分层总和法、基于本构理论的数值计算法和基于实测数据的预测法.由于路基工后沉降的影响因素较多,路基土的物理力学参数难以精确测定,因此,分层总和法和数值计算法的预测精度受到很大限制[3].基于实测数据的预测法是通过先进监测手段获得路基沉降数据,并基于小波去噪分析、线性回归分析、灰色系统理论分析、人工神经网络或支持向量机等数学模型对路基沉降进行预测,具有预测精度高、计算过程简单等优点.
众多学者采用基于实测数据的预测法开展了沉降预测研究.颜早璜等采用双曲线拟合了路基拓宽荷载造成的路面沉降[4].Yang等以京沪高铁济南段为例,基于线性CCD方法建立了高铁路基沉降预测模型[5].郭健等以武汉某深基坑工程的监测数据为基础,提出了预测工后沉降的小波分析与径向基神经网络混合建模方法[6].肖衡林等分别采用时间对数、泊松曲线和指数曲线方法建立了鄂西某67m高路堤的沉降预测模型[7].谭衢霖等针对某高层混凝土结构建立了改进的BP神经网络、辅助式小波神经网络和嵌入式小波神经网络变形预测模型[8].朱才辉等以某黄土高填方地基为例,建立了基于修正FDA分析的工后沉降计算模型[9].Chen等提出了地下水位下降引发的高铁路基沉降数值计算方法[10].高红等提出了基于小波变换与卡尔曼滤波相结合的RLG降噪方法,并采用GM(1,1)算法建立了沉降预测模型[11].章红兵等基于沉降监测数据,提出了考虑空间效应的紧邻基坑建筑物沉降简化算法[12].
青岛-连云港高速铁路(以下简称青连高铁)部分路基的工后沉降较大,对高铁安全运行产生较大危害[13].本文在借鉴已有研究的基础上,以青连高铁K104+080路基为例,通过设计合理的监测方案开展路基工后沉降监测,在验证GM(1,1)模型、神经网络模型和灰色神经网络模型预测精度的基础上,选取灰色神经网络建立路基工后沉降预测模型,预测了该路基工后沉降量并提出了分级预警方法.
1 路基工后沉降监测方案与数据分析
1.1 工程概况与监测方案
青连高铁是我国“八纵八横”综合运输大通道的重要组成部分,与盐通铁路、连盐铁路、沪通铁路无缝对接,建成后将成为青岛至上海的铁路通道,正线长194.39 km,总投资238亿元.沿线区域自然地貌的地带性差异显著,地质条件复杂,在降雨、冻融作用下,易产生较大工后沉降[13].青连高铁为无砟轨道,根据国内外高铁建设的经验可知,无砟轨道的工后沉降一般不应超过15 mm,否则会对行车安全造成较大危害.青连高铁K104+080路基位于奎山站附近,对该路基工后沉降进行监测和预测对保证高铁安全运行具有重要意义.
该路基从上至下依次为道砟层、水泥改良土层、压实土层、水泥改良土层和挤密桩稳定水泥土层,采用半断面监测方式,监测范围为路基顶面至挤密桩稳定水泥土层顶面以下2 m,采用分层沉降计、单点沉降计和土壤水分计监测路基不同部位的工后沉降、沉降速率和湿度.
(1)分层沉降计:设置3组分层沉降计,每组设置4个监测点,监测点从上至下分别距路基顶面0.5、1.3、3.1和5.9 m.
(2)单点沉降计:设置一组单点沉降计,位于坡脚处,埋深0.2 m.
(3)土壤水分计:设置3组土壤水分计,每组设置3个监测点,监测点从上至下分别距路基顶面1.2、1.7和2.2 m,监测方案如图1所示.
图1 青连高铁K104+080路基监测方案
监测时间从2016年9月1日起~2017年11月16日止,每月1日、16日读取一次数据,读数时间为凌晨3时(此时无列车通过),至今已获取30期、660项监测数据.
1.2 监测结果分析
限于篇幅原因,本文仅以第Ⅰ组分层沉降计为例分析路基工后沉降监测结果并进行路基工后沉降预测.在监测期内,Ⅰ-1、Ⅰ-2、Ⅰ-3和Ⅰ- 4监测点的工后沉降分别为5.07、4.83、4.59和4.35mm,沉降速率最大值分别为第21监测期(2017年7月1日)的0.43 mm、第21监测期的0.36 mm、第22监测期(2017年7月16日)的0.32 mm和第23监测期(2017年8月1日)的0.25 mm.四个监测点的工后沉降在第9、10监测期(2017年1月1日、16日)出现减小趋势,分别减小0.08和0.03 mm.
根据对路基工后沉降监测数据的分析可知,路基工后沉降具有以下规律:
(1)降雨和温缩作用对路基工后沉降影响较大.根据气象资料,该路基所在区域的年均降雨量约为650 mm,其中,7月~9月降雨量约占全年降雨量的60%.路基沉降速率在7、8月达到最大,可见路基工后沉降与降雨量呈显著的正相关关系.路基工后沉降在1月出现减小趋势,主要原因为1月温度较低且降雨量较小,路基土体出现温缩现象,导致路基工后沉降减小.
(2)路基工后沉降具有明显的时空分异特征.沉降量从路基土体上部向下逐渐减小,在沉降发生时间上路基土体下部滞后于土体上部.
2 路基工后沉降预测
2.1 预测方法概述
由于监测时间较短,要明确该路基未来的稳定状况,必须根据已有监测数据开展路基工后沉降预测研究.常用的路基工后沉降预测方法包括GM(1,1)模型和神经网络模型.GM(1,1)模型是由邓聚龙教授提出的,它将待估系统视为部分信息已知、部分信息未知的灰色系统[14].在进行灰色系统预测时,GM(1,1)模型具有对已知序列要求低、计算过程简单等优点,但当预测期较长时,GM(1,1)模型的预测精度出现明显退化.神经网络模型是数据序列预测最常用的方法之一,它通过已知序列对神经网络的训练达到模拟人脑决策过程的效果,具有预测精度高、容错能力强等优点[15],但对模型训练序列要求较高,否则易陷入局部极小值或难以收敛.灰色神经网络模型是GM(1,1)模型与神经网络模型的串联算法,可以克服GM(1,1)模型和神经网络模型的缺点,其基本思路是将GM(1,1)模型预测结果输入神经网络进行训练,待网络稳定且实现收敛后利用训练好的网络进行路基工后沉降预测.
2.2 模型验证
监测期和相应的监测值组成数据对,Ⅰ-1、Ⅰ-2、Ⅰ-3和Ⅰ-4监测点共计组成120个数据对,其中,4个监测点第30期监测数据组成的数据对分别为(30,5.07)、(30,4.83)、(30,4.59)和(30,4.35).分别采用GM(1,1)模型、神经网络模型和灰色神经网络模型开展路基工后沉降预测,将前25期监测数据对作为已知序列,后5期监测数据对作为验证序列.三种模型的验证序列预测值和实测值对比如表1所示.
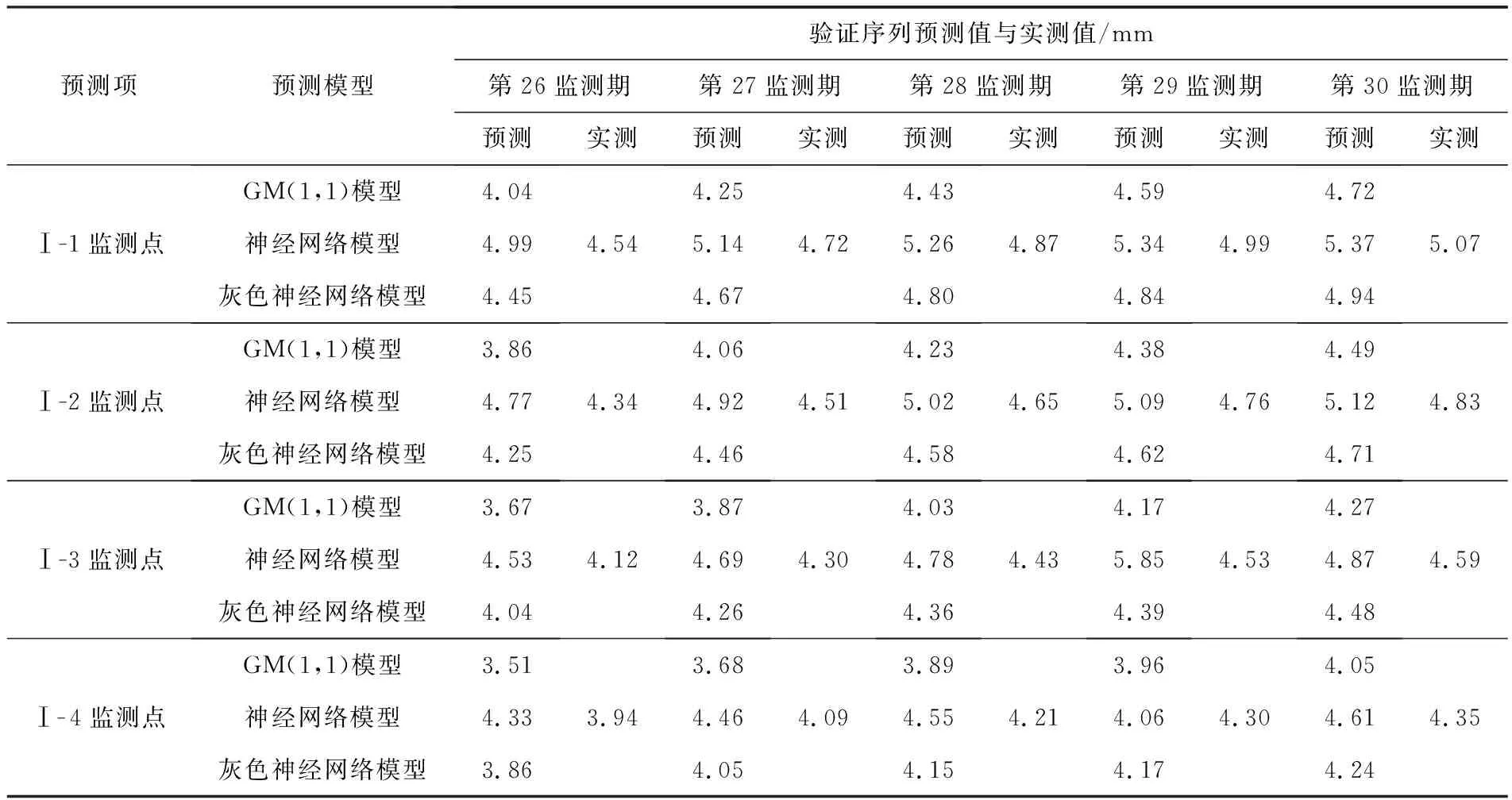
表1 验证序列预测值与实测值对比
由表1可知,GM(1,1)模型、神经网络模型和灰色神经网络模型对应的预测值与实测值最大相对误差分别为11.17%、8.03%和5.46%,预测精度均满足要求.为评判各模型的预测效果,根据表1的数据计算3种模型预测值与实测值的均方误差(Mean Squared Error,MSE),如表2所示.
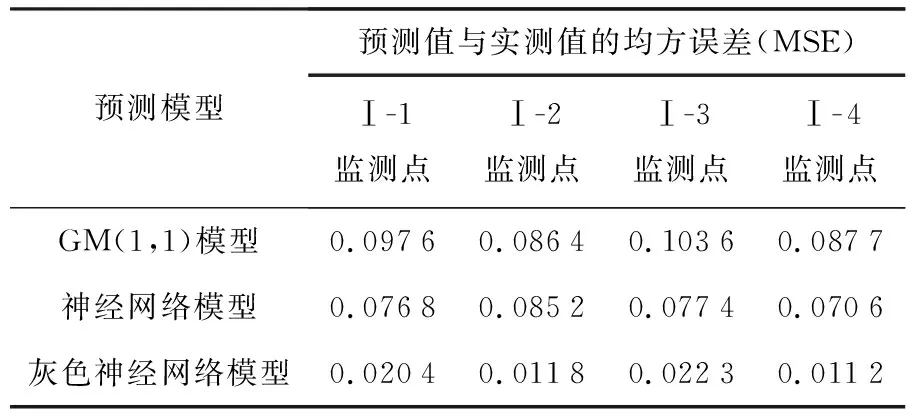
表2 三种模型的均方误差
由表2可知,4个监测点的预测结果中,灰色神经网络模型的预测效果均最好,神经网络模型次之,GM(1,1)模型最差.因此,本文选取灰色神经网络模型预测青连高铁K104+080路基工后沉降.
2.3 预测结果
采用灰色神经网络模型预测青连高铁K104+080路基第31~50监测期的工后沉降,预测结果如表3、图2所示.
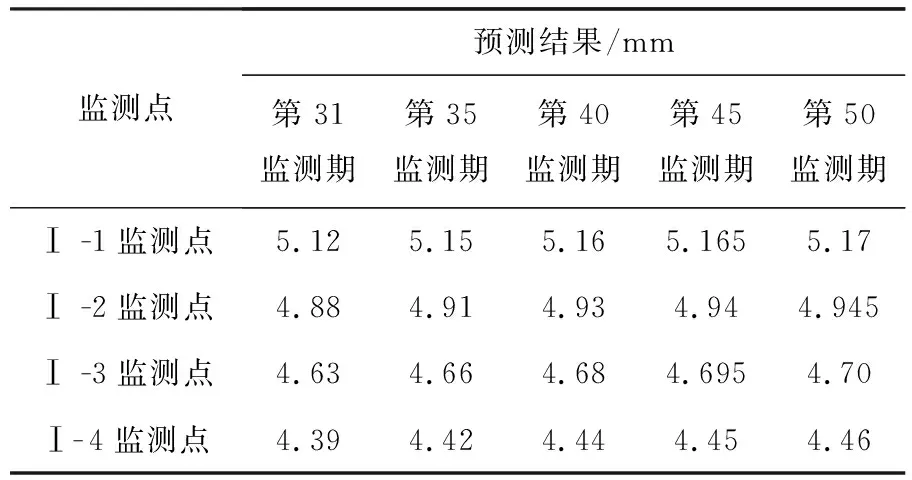
表3 工后沉降预测值

图2 工后沉降预测值
由表3、图2可知,Ⅰ-1、Ⅰ-2、Ⅰ-3和Ⅰ-4监测点的工后沉降预测值在第45监测期以后增量很小,并分别收敛于5.19、4.96、4.71和4.47mm,均远小于15 mm.可见,在没有其他诱发因素作用下,该路基将继续保持稳定状态.
2.4 路基工后沉降预警
第Ⅰ组分层沉降计4个监测点的工后沉降最大值收敛于5.19 mm,即路基工后沉降不会对行车安全造成重大威胁.但是,这种稳定是有条件的,如果发生大量水体下渗、地基开挖或地震等特殊工况,该路基的工后沉降可能发生突变,从而威胁行车安全.因此,必须对高铁路基工后沉降进行分级预警,本文根据已有路基工后沉降研究并结合青连高铁的工程实际,选取工后沉降量为主要预警指标,沉降速率为辅助预警指标,设定Ⅰ、Ⅱ、Ⅲ级预警等级,如表4所示.

表4 预警等级划分
以工后沉降量为首选预警指标,当工后沉降量变化较剧烈时,以沉降速率为辅助预警指标.其中,Ⅰ级预警表示路基较安全,不需要发布预警信息;Ⅱ、Ⅲ级预警分别表示较危险和危险,需要发布预警信息.
3 结论
(1)以青连高铁K104+080路基为例,通过设计合理的监测方案开展了路基不同部位的工后沉降、沉降速率和湿度监测,分析了路基工后沉降规律.在验证GM(1,1)模型、神经网络模型和灰色神经网络模型预测精度的基础上,采用灰色神经网络模型建立了路基工后沉降预测模型,提出了路基工后沉降预警方法;
(2)Ⅰ-1、Ⅰ-2、Ⅰ-3和Ⅰ- 4监测点的工后沉降预测值在第45监测期以后增量很小,并分别收敛于5.19、4.96、4.71和4.47 mm,该路基将继续保持稳定状态.选取工后沉降量为主要预警指标,沉降速率为辅助预警指标,将高铁路基沉降预警等级分为Ⅰ、Ⅱ和Ⅲ级;
(3)本文开展了青连高铁K104+080路基工后沉降监测与预测研究,但在以下方面仍可改进:①本文仅开展了第Ⅰ组分层沉降计监测数据的分析与预测,单点沉降计和土壤水分计监测数据的分析与预测未开展,路基工后沉降与土体湿度的关系也未开展研究;②本文采用灰色神经网络模型建立了路基工后沉降预测模型,预测精度虽能满足要求,但其他算法,如小波分析、PSO-ANN模型以及PSO-SVM模型等的预测精度未得到验证.

