矩形简支薄板振动模态及灵敏度分析
王秀颖,张军,兆文忠
(大连交通大学 交通工程学院,辽宁 大连 116028)
0 引言
振动模态是结构的固有动力学性能,模态频率及振动模式直接影响工程结构的动力学性能、安全性及稳定性,尤其薄板结构的模态特性更直接与振动强度、噪声及疲劳性能密切相关,薄板类结构也是车辆、船舶等工程中广泛使用的基本结构之一[1-2],对薄板类结构的研究主要是针对薄板类结构的振动及噪声[3-5].为了减小振动,在工程设计阶段一般会对结构进行修改,快速准确的修改需要计算结构灵敏度[6-8],结构灵敏度是结构模态、应力等响应随结构参数的变化率,即响应对结构设计变量的导数.在有限单元法的基础上,灵敏度计算方法有解析法[9-10]、半解析法[11]、完全差分法[12]、伴随变量法等[13-14].解析法是从有限单元方程出发,严格求响应对设计变量的导数,对不同的单元类型及不同的结构参数,其理论是完全不同的,如壳单元和梁单元中的质量矩阵和刚度矩阵完全不同,其对结构参数的灵敏度也是完全不同的.解析法发展最早,精度最高,但求解效率低.半解析法是在有限单元法的基础上,总体上基于有限单元方程用微分法求对结构参数的灵敏度,但质量矩阵和刚度矩阵对结构参数的灵敏度用差分法,不用考虑具体的矩阵形式,提高了计算效率,并具有较高精度,这种方法兼顾求解效率和求解精度,是普遍使用的方法之一.完全有限差分法求解灵敏度不必进行复杂的理论推导,具有很大的通用性,但是对N个设计参数求解结构响应的灵敏度必需进行N+1次响应计算,计算效率低,而且所求得的灵敏度依赖于差分步长,计算精度也较低.伴随变量法是通过伴随变量,解决求解具有大规模设计变量灵敏度的求解效率问题. 张保[15]提出了半解析伴随变量灵敏度计算方法,以四边简支平板为算例,验证了计算精度和效率高于一般伴随变量法.程耿东院士[16]以梁结构为研究对象,用半解析法计算了模态灵敏度,并分析了半解析法的误差.
本文以矩形简支薄板为研究对象,推导了模态的理论解,并推导出了模态频率对薄板厚度的灵敏度计算式,即简支矩形薄板的模态灵敏度理论解,并计算了基于理论解的模态频率差分解.建立了简支矩形薄板的有限元模型,用有限单元法计算了其振动模态,基于有限元法用半解析法计算了模态频率对板件厚度的灵敏度,并计算了基于有限元法的完全差分模态频率灵敏度.
1 简支薄板模态基本理论
1.1 简支矩形薄板的模态
矩形简支薄板的几何模型如图 1所示.

图1 简支矩形薄板几何模型
薄板长和宽分别为a、b,厚度为h.设其在z方向的振动位移为w,则薄板的振动平衡方程为
(1)

(2)
通过分离变量法[17],可求得薄板的横向频域自由振动方程为
(3)

(4)
(5)
式(5)表明,矩形简支振动薄板的特征频率与材料参数、板厚度及矩形边长有关.
1.2 矩形简支薄板模态频率灵敏度
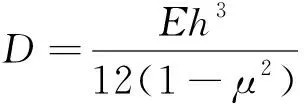
(6)
通过式(6)表示的模态频率求对薄板厚度h的导数,即薄板模态频率灵敏度的理论解,表示为
(7)
式(7)表明,矩形简支薄板的模态频率对板厚度的灵敏度的理论解与板厚度无关.
2 基于有限单元法模态及其灵敏度
模态频率灵敏度即结构自由振动频率随结构参数的变化率.模态频率灵敏度可以用结构自由振动模态方程对设计变量进行微分得到.无阻尼结构自由振动有限元方程表示为
([K]-λi[M]){φi}=0
(8)
式中,[K]、[M]分别为结构刚度矩阵和结构质量矩阵;λi为结构第i个特征值,{φi}为结构第i个振型向量.
设第j个设计变量为xj,式(8)对其求导数

(9)
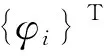
(10)
由式(9)、(10)得模态频率灵敏度为
(11)

(12)
3 振动薄板的模态频率
设简支矩形薄板厚度为h,两个边长分别为0.33 m和0.2 m,材料为钢材,弹性模量E为210GPa,泊松比μ为0.31,密度ρ为7 800 kg/m3.为了研究模态频率及其灵敏度,分别用式(6)、(7)计算了薄板的模态频率及其灵敏度理论解,并用有限单元法进行了同样的计算.
3.1 模态频率的理论解
按照式(6)厚度分别为0.9、1.0、1.1 cm的矩形简支薄板的前十阶模态频率理论解被列在表1中.表1表明,随着板厚度增加模态频率逐渐增加.在表2中.

表1 简支薄板的模态频率 Hz
3.2 模态频率的有限元解
建立简支薄板的有限单元模型,如图2所示.为了避免有限单元网格数量的影响,研究了网格数量对计算结果的影响,对0.3 m×0.2 m、1 cm厚的简支矩形薄分别板划分了24、300、600、1200、2 400个四边形壳单元, 不同单元数量的模态频率被列表2表明当网格数量达到600个单元以上时,计算的1阶模态频率已经相同,高阶模态频率之间的误差已经很小,与理论解的误差也相对不再减小,可以认为600单元的有限单元解已经相对准确了. 前4阶模态振型如图3所示.

图2 有限单元模型
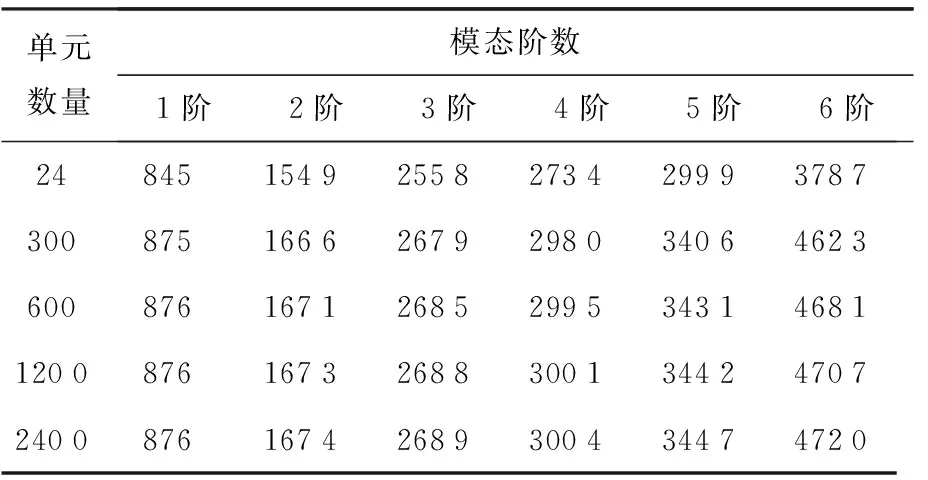
表2 不同网格数量简支板模态频率 Hz
图3 简支矩形薄板前4阶模态振型
3.3 模态频率误差分析
为了分析简支矩形薄板模态频率有限元解与理论解之间的误差,同样用有限单元法计算了厚度分别为0.9、1.0、1.1 cm的简支薄板的前10阶模态,前5阶数值解模态频率、理论解模态频率及之间的误差被列在表3中,有限元网格为600个单元.表3表明,随着板厚度增加有限元数值解与理论解的误差增加,随着模态阶数增加误差也增加.前10阶模态频率有限元数值解与理论解的误差百分比如图4所示.

表3 前5阶频率有限元解、理论解及差值 Hz

图4 模态频率有限元解与理论解误差
图4表明,虽然总体来看随着模态阶数及模态频率的增加,简支矩形薄板有限单元解与理论解之间的误差增加,但是误差随着模态阶数的变化存在峰值,在有些模态误差会出现较大的峰值.
4 模态频率灵敏度
利用式(7)可以计算简支矩形薄板模态频率灵敏度的理论解,灵敏度理论解与厚度无关,并不随板厚度的改变而改变,将其定义为s1,同时可以利用理论计算的不同厚度简支薄板的模态频率计算出理论差分灵敏度,0.9~1.0 cm的理论模态差分灵敏度定义为s2, 1.0~1.1 cm的理论模态差分灵敏度定义为s3.利用有限元法求得的不同厚度模态频率也可以求出灵敏度差分解,0.9~1.0 cm的有限元模态差分灵敏度定义为s4,1.0~1.1 cm的有限元模态差分灵敏度定义为s5.利用式(11)和式(12)可以求出采用基于有限元法的半分析的数值微分法模态灵敏度,板厚度不同模态灵敏度是不同的,板厚度分别取0.9、1.0、1.1 cm的半分析数值微分灵敏度分别定义为s6、s7、s8. 利用三个不同的板厚度可以计算出8个模态频率灵敏度值,前5阶模态频率对板厚度的灵敏度被列在表4中. 表4表明,一阶模态灵敏度的理论差分解与理论解相差最小,半分析的数值微分解与理论误差最大;但随着模态阶数的增加,理论差分解和有限元差分解与理论解的误差逐渐增大,而半分析的数值微分解与理论解的误差却逐渐减小,到第4阶模态时,数值微分解与理论解的误差最小;理论差分解、有限元差分解与理论解之间的误差大致相同.用数值微分法计算的不同薄板厚度的灵敏度s6、s7、s8几乎是相同的,这与理论灵敏度类似,即矩形简支薄板模态频率对板件厚度的灵敏度与厚度无关.

表4 模态频率灵敏度 Hz/mm
板厚度为0.9 cm前10阶模态频率灵敏度如图5所示.图5表明,1、2阶模态频率灵敏度理论差分解和有限元差分解与理论值的误差较小,但从第2阶开始,差分解于理论解之间的误差几乎呈线性增加,到第10阶时其误差已经超过100%;从第3阶模态开始,基于有限单元的数值微分法的模态频率灵敏度与理论解之间的误差最小,而且在全部10阶模态灵敏度来看,其误差均在合理范围内.
图5 0.9 cm简支薄板模态频率灵敏度
5 结论
(1)基于简支矩形薄板的模态理论计算式,推导了模态频率对薄板厚度的灵敏度,理论计算式表明,简支矩形薄板模态频率对薄板厚度的灵敏度与薄板厚度无关;
(2)用理论差分法、有限单元差分法和基于有限单元的半分析数值微分法分别计算了薄板模态频率对薄板厚度的灵敏度,计算结果表明只有第1阶模态频率差分模态灵敏度与理论解误差较小,从第2阶模态开始,其与理论解之间的误差几乎呈线性递增;而基于有限单元的半分析数值微分模态灵敏度与理论解之间的误差均在合理范围内,证明了半分析数值微分法模态灵敏度的有效性和准确性;
(3)取不同的薄板厚度时,基于有限单元的半分析数值微分模态灵敏度几乎相同,这与模态灵敏度理论计算式的结论是相同的,即简支矩形板模态频率对薄板厚度的灵敏度与厚度无关,这进一步验证了半分析数值微分法模态灵敏度的正确性.

