铁路行包运到期限确定方法研究

荣文竽，王泽,魏玉光

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028；2.北京交通大学 交通运输学院，北京 100044)

0 引言

物流经济条件下，快递业高速发展，以小件运输为主的铁路行包运输面临竞争与挑战.依托铁路运输的小件货物运输具有成本和安全优势，但与其他快递业相比，铁路行包运到期限规定落后，与当前铁路行包运输实际不符，不适应货主对运输时效的需求.如何科学合理地确定铁路行包运到期限，是制定行包运输组织方案和运输合同的依据，也是提高铁路行包运输竞争力的重要途径.

目前，国内在行包运到期限方面没有专门的研究，行包运输主要在行包运输组织、票据及营销策略等方面开展研究[1-3]；运到期限方面的研究主要集中于货物运输上，通过分析货物运输过程，提出货物送达期限的评估方法[4].国外铁路行包运输主要关注技术装备和信息技术的应用方面[5]，对运到期限没有规定.

本文从行包运输实际出发，运用大数据及数理统计等方法，对铁路行包运到时间变化规律进行研究，提出更加科学合理的铁路行包运到期限的确定方法.

1 问题的提出

1.1 基本概念

行包运到时间是指行包从承运时起至到达目的站卸车完了时止的全部时间.考虑行包卸车作业一般都是在列车停靠的站台上即时完成，所以，可以认为行包运到时间主要包括始发站停留时间、中转站停留时间和在途运行时间三部分.其中始发站停留时间指行包在始发站自承运至随旅客列车由车站发出止的停留时间；在途运行时间指行包随列车在区间运行的全部运输时间；中转站停留时间指自行包到达中转站至再次发出时止的中转停留时间.

行包运到期限是指铁路运输部门规定的行李、包裹运输一定里程所需要的时间标准.这个期限是根据现有技术设备和运输组织水平，分别按行李和包裹确定的.与铁路货物运到期限相类似，一般规定行包托运方发出托运请求当天算一日，行包承运方在终到站的指定地点卸车完成时间为运到期限的截止时间.

1.2 目前行包运到期限规定存在的问题

原铁道部1997年12月1日发布的《铁路旅客运输规程》第79条，对行包运到期限的计算方法作出了明确的规定：行李、包裹的运到期限以运价里程计算.从承运日起，行李600 km以内为三日，超过600 km时，每增加600 km增加一日，不足600 km也按一日计算.包裹400 km以内为三日，超过400 km时，每增加400 km增加一日，不足400 km也按一日计算[6].

随着我国铁路基础设施建设，特别是最近十年来高速铁路的发展，20年前的行包运到期限规定已经不适应目前铁路行包运输实际，不能作为铁路运输部门进行行包运输的有效规定，也不能适应货主对行包运输时效性的要求.

1.3 行包运到期限确定的基本思路

行包的实际运到时间受到运输组织模式、在装卸站的生产作业过程、中转作业次数、经由径路通过能力、列车运行速度、运送距离等因素影响.根据运输组织模式将行包运输过程可以分为两类，其一是采用直达方式(始发直达、行包专列等运输组织模式)的运送过程，其二是非直达，即中转方式的运送过程.

直达行包运到时间，主要包括始发站停留时间和在途运行时间；中转行包运到时间，主要包括始发站停留时间、中转站停留时间和在途运行时间.无论采取哪种运输组织方式，分别通过对行包在始发站停留时间、中转站停留时间和在途运行时间的历史数据进行抽样统计分析，找出其变化规律，建立行包运到时间的拟合方程.在此基础上，选择一定置信度水平，建立行包运到期限确定方法.

2 抽样样本分析

2.1 抽样方法

选取铁路行包管理系统中的货物追踪信息为调查对象，抽样方法为简单随机抽样.随机以行包票全票号的末六位数字为索引，从2015年4月至2017年4月的行包追踪信息中随机抽出共计1417批数据，数据包括始发站、到站、运价里程、承运制票时间、始发车次、装车时间、中转站、中转站卸车时间，中转站装车时间、中转站装车车次、终到站卸车时间等反映行包实际运输过程的有关信息.样本的始发、中转、终到站涵盖了全路18个铁路局和集团公司.样本的时间跨度的覆盖了三年四个季度.样本容量(n)满足检验要求的最小数量[7](n>50).

2.2 样本筛选

通过样本分析和对行包运输实际调查发现，个别数据可能由于信息系统录入或其他原因，导致数据严重失真.为了尽可能保证所研究数据的真实性，有必要对样本进行筛选.

(1)通过分析技术速度剔除严重失真数据.一般来说，以目前的设施设备和技术条件，行包运输的技术速度应分布在一个合理范围内.通过对抽样的样本数据分析，技术速度过高(超过200km/h)或过低(低于30 km/h)均是不合理的，因此有必要对这类异常的样本值进行剔除.按该条件，剔除了20条异常数据，占样本数1.4%.这些数据产生的原因可能是系统数据生成错误或者由于特殊原因导致的运输过程异常.

(2)通过分析站停时间异常剔除严重失真数据.样本分析发现，行包运输中在始发站和中转站停留时间长短取决于车站的行包办理量、列车到开时刻、装卸作业时间等因素，也有的由于在运输繁忙期或是自然灾害、行车事故等原因造成的行包积压，也会导致个别行包在始发站或中转站超时停留.因此，行包在站停留时间长是正常现象.但是，样本分析发现，有1条样本数据显示行包在中转站停留时间是负数，这在实际中是不合理的，作为异常数据预以剔除.从这方面分析剔除数据1条，占样本数0.07%.

(3)不可抗力的原因、托运人责任等因素和主观因素也会造成行包运到时间异常，但由于这种情况难以判别，并且属于小概率事件.因此，在样本筛选中暂不考虑这类数据的剔除.

3 行包运到时间的统计及回归分析

通过对实际的行包运输作业过程调查分析发现，行包的始发站停留时间主要受托运人发出行包托运请求的时间、装运行包列车的出发时间和办理行包托运时间等因素影响；行包的中转站停留时间主要受中转次数、列车正点率和到发时刻、行包装卸时间等因素影响；行包在途运行时间主要与运价里程和装运行包的列车等级和速度相关.可以通过分析行包在始发站、中转站的停留时间，发现其统计规律，确定行包的始发站、中转站停留时间标准.行包的在途运行时间主要跟运输距离相关，一般情况下，运输距离越远，行包的在途运行时间越长，但是也不一定是目前《铁路旅客运输规程》规定的以400或600 km为单位的分段函数关系.运用回归分析理论，在一定的置信度水平下，确定行包在途运行时间与运价里程的相关关系，找出其变化规律，建立函数关系模型，能够得到合理的行包运到期限的确定方法.

3.1 行包在始发站、中转站停留时间的统计分析

经统计，行包在始发站停留时间累积分布如图1所示，行包在中转站停留时间累积分布如图2所示.

图1 始发站停留时间的累积分布

图2 中转站停留时间的累积分布

可以看到，样本内84.9%的始发站停留时间、93.93%的中转站停留时间在1日以内，根据实际铁路行包运输过程，可以认为行包在始发站、每个中转站停留时间为1日是正常的行包作业过程，可以作为行包的始发站、中转站停留时间标准.

3.2 行包在途运行时间的回归分析

假定行包在途运行时间(T)与计价运输距离(Li)的回归关系为：T=f(Li)+ε，其中Li是可以精确测定并可控制的变量，f(Li)是T对Li的回归方程，且存在多阶可微；ε是随机误差，且E(ε)=0，Var(ε)=σ2；那么总存在T关于Li的一元回归方程.设T的回归模型为：

T=β0+β1Li+ε

(1)

3.2.1 回归分析步骤

(1)在给定的样本基础上，按最小二乘法，求出β0，β1，得到相应的回归方程：

(2)

(2)计算决定系数(R2)和复相关系数(R).对回归方程进行显著性分析，一般R2、R越接近1，回归方程的拟合优度越高.当然，拟合优度并不是检验模型优劣的唯一标准.

R2=S回/S总

R=(S回/S总)1/2

(3)

(3)进行回归方程的显著性检验.假设H0:β1=0，如果H0被接受，则表明式(2)不合适，根据回归方程显著性检验理论[7]，计算F统计量：

(4)

在给定显著性检验的可靠度(1-α)条件下(一般认为α取0.05符合现实要求)，查F分布表，得临界值Fα；如果F>Fα，则拒绝H0，认为回归效果是显著的；否则认为回归关系不显著.

(4)确定预测区间上限函数.预测区间是预测区间上限函数(UPL)与预测区间下限函数(LPL)包含的数据区域.在给定置信水平(1-α=0.95)下，得到的预测区间为：

考虑到目前的铁路行包运输成本和逾期赔付机制，将预测区间上限函数(UPL)应用于行包在途运行时间的确定是比较合理的.

3.2.2 行包在途运行时间的回归分析

(1)回归方程

运用Origin软件，对样本的行包在途运行时间进行回归分析，样本散点和拟合曲线见图3，得到T的回归方程为：

(5)

(2)样本决定系数(R2)和复相关系数(R)

依据样本和回归方程式(5)，按式(3)定义得到：

n=1397，S残=194.94，S回=352.91，S总=547.85，R2=0.64，R=0.80.

从回归分析结果看，样本的复相关系数为0.8，一方面可以看出全路相同运输距离的行包在途运行时间的变化范围较大，另一方面也体现了行包在途运行时间与运价里程这一单因素的关联性特征.

(3)回归方程的显著性检验

依据样本和回归方程式(5)，回归自变量个数(p)为2；按式(4)可计算出：

在给定显著性检验的可靠度1-α=0.95条件下，查F分布表，得临界值F0.05(2,1394)=3.0；显然F>F0.05，拒绝H0，即回归方程(式5)的回归效果显著.

图3 样本散点和拟合曲线

(4)95%预测区间上限函数的确定

根据拟合曲线得到的拟合方程式(5)，在95%的置信度水平下，得到的预测区间上限函数为：

(6)

因此，在95%置信水平条件下，行包在途运行时间上限值可由式(6)确定.

4 铁路行包运到期限的确定

我国铁路发展早期，铁路行包运输中行李运输占有一定的比例，而且行李运输一般较包裹运输速度快.现行的《铁路旅客运输规程》把行李和包裹分开确定运到期限.随着人们出行方式的改变，目前，行李运量仅占2%左右，而且呈逐年递减趋势.建议对于行包运到期限的确定，不再区分行李、包裹.按照同样的时限标准承诺行包的运到期限.

根据上述统计和回归分析方法，结合我国铁路行包运输生产技术设备条件和运营生产组织的特点，认为现行《铁路旅客运输规程》对运到期限的规定明显偏大.建议按照数据统计分析结果确定的方法，对现行铁路行包运到期限进行调整.

调整后的行包运到期限按下式确定：

T=x+n+|f(Li)|

(7)

其中:T为行包运到期限；x为行包始发站停留时间，x=1；n为行包中转次数；f(Li)为行包在途运行时间的95%预测区间上限函数， “ 「⎤ ”为向上取整函数.

由式(6)得：

(8)

由式(8)得到直达行包运到期限的确定方法，如表1所示.

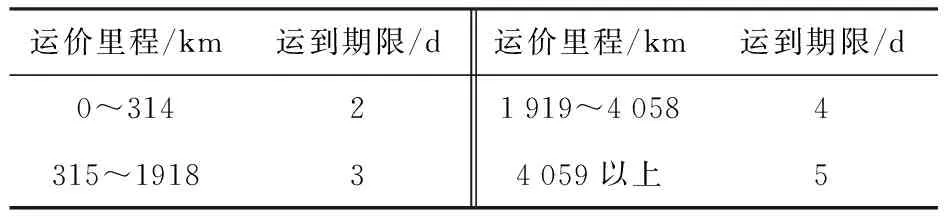
表1 直达行包运到期限确定方法

此外，中转行包每中转一次，运到期限需在此基础上额外增加1日.

根据我国铁路行包运输的实际情况，为了使该方法更简洁明了，易于推行，可对铁路行包运到期限简化规定：行包运到期限以运价里程计算.从承运日起，400 km以内为2日；超过400 km、不足2 000 km为3日；超过2 000 km、不足4 000 km为4日；超过4 000 km时，一律按5日计算.行包在途径车站每中转一次，行包运到期限还需额外增加1日.

以直达行包为例，现行和调整后的行包运到期限对比见图4.

图4 现行和调整后的行包运到期限对比

由图4可以看到，调整后的行包运到期限曲线不仅能够基本涵盖了抽样样本内行包实际运到时间的绝大多数散点，而且，与现行《铁路旅客运输规程》规定的运到期限相比，调整后的运到期限确定方法更符合铁路行包运输实际，也更能体现行包运输的时效性.

与现行《铁路旅客运输规程》规定的行包运到期限相比，同等里程范围内，调整后的运到期限确定方法缩短的运到期限日数见表2.

表2 调整后的运到期限确定方法缩短的日数

综上，与现行规定相比，调整后的行包运到期限更能反映我国铁路行包运输实际，而且具有显著的时效性优势.

5 结论

本文通过统计分析，利用回归分析的方法得到行包在途运行时间的回归方程，建立一定置信水平下的行包运到期限计算方法，得到更为科学合理的铁路行包运到期限的确定方法.一方面，为行包运到期限的预报或估计提供科学理论依据；另一方面，与现行《铁路旅客运输规程》规定的运到期限相比，本文得出的运到期限确定方法更符合铁路行包运输实际，也更能体现行包运输的时效性.此外，还可以通过改变行包在途运行时间上限函数的置信区间，调整行包按期到达的可靠性.

需要注意的是，数据分析建立在有限的行包追踪信息样本基础之上，由于受到样本容量的影响，数据分析的精度可能会受到一定程度的影响.