低碳木材物流网络优化中的碳排放测度
陈 诚, 邱荣祖(福建农林大学交通与土木工程学院,福建 福州 350002)
随着气候问题的日益恶化,全球化的“低碳革命”正在兴起;同时,近年来物流业能源消耗一直呈增长趋势,是我国二氧化碳排放增速最快的行业之一[1].发展低碳物流是实现低碳经济的前提和基础[2],木材物流作为物流行业的一个专门类别,其生产和供应与具有重要碳汇价值的森林[3]的经营计划密切相关,因而更与低碳经济、生态建设密切相关.
在木材物流[4]过程中,按运动程度的不同可以划分为运动过程和停顿过程,运动和停顿过程构成了木材物流网络.木材物流网络的有效设计和优化能在很大程度上缓解传统木材物流存在的舍近求远、迂回运输以及运力浪费、成本过高等问题[5,6],也有利于供应链整体效率的提升[7].
木材物流网络碳排放的合理测度是低碳木材物流网络优化的前提,本文探讨木材物流网络碳排放的合理测度,并揭示不同测度方法对优化结果的影响,旨在为低碳物流网络优化中碳排放测度方法的选择提供参考.
1 木材物流网络碳排放测度
在木材物流网络中,碳排放主要来自于木材加工作业和木材运输作业的能源消耗[8].
1.1 与节点有关的碳排放测度
在物流网络中,节点的形态有很多种,可能是制造厂商、配送中心、仓库、转运中心、客户,也可能是回收中心、处置中心等.对于不同形态的节点,由于功能不同,碳排放的主要影响因素也不同.如冷链物流网络中的物流节点,由于需要更多的能源对仓储空间进行制冷,比一般货物物流网络中的物流节点产生的碳排放更多[9].此外,就同类节点来说,作业量越多,碳排放量也越多.
从基于活动的能源消耗角度对木材物流网络节点(木材物流中心)进行碳排放分析,木材物流中心作业流程如图1所示,其中检验检疫也可能在伐区楞场进行,故用虚线框表示.

图1 木材物流中心作业流程图Fig.1 Procedure of operations in timber logistics center
首先,从仓储属性上看,由于木材物流中心所储存的货物无需特殊仓储环境,如加热或冷却,因此可以根据木材物流中心的规模估算其年固定碳排量(式(1))[10];而单位规模的碳排放系数与节点规模成凹函数关系[11].
σ1=V·f1(V)
(1)
式中,σ1表示木材物流中心的固定碳排放量,V表示木材物流中心规模,f1(.)表示木材物流中心单位碳排放量系数函数.
木材物流中心的变动碳排放主要来自于加工作业所需的能源消耗.初加工作业若未在物流中心进行(如采取直送模式的木材),则将在客户处进行,因此若考虑了木材物流中心处加工作业产生的变动碳排放,也应该将客户处的木材加工作业产生的碳排放量算到木材物流网络的碳排放中.节点(包括木材物流中心和需材点)处的变动碳排放可由式(2)计算.
σ2=TV·f2(TV)
(2)
式中,σ2表示木材物流中心和客户处的变动碳排放,TV表示加工作业量,f2(.)表示单位作业量的碳排放系数函数.
木材物流中心转运比直接运至客户处的作业活动增加了1次装卸作业,此部分碳排放体现在木材物流中心的变动碳排放测度中.
1.2 与线路有关的碳排放测度
物流网络中线路上的碳排放主要来自于线路上货物运输产生的碳排放,即来自于运输车辆的能源消耗.而运输车辆能源消耗的主要因素影响大致可以分为三类:车辆设计技术参数、行驶环境参数及驾驶员行为[12].其中,前两项为可控因素,最后一项为不可控因素.基于前两项因素,木材物流网络的线路碳排放可以根据车型、道路状况和区域气候确定.文献[13]提出的综合排放模型(式(3)~(5)),包含了几乎所有的可控参数,且经道路试验证明能较准确地估算货运车辆的能源消耗,故被广泛应用[14].
e=F·δ
(3)
F≈FR·(d/v)
(4)
(5)
式中,e表示路线上的碳排放,F表示路线上的燃油消耗量(J),δ表示燃料的排放系数(t·J-1),FR表示车辆的燃油消耗率(J·s-1),d为路线长度(m),v为车辆的行驶速度(m·s-1),k为发动机摩擦系数(J·r·L-1),N发动机转速(r·s-1),V为发动机排量(L),M为汽车整备质量(kg),f为汽车载重量(kg),a为车辆的加速度(m·s-2),g为重力加速度常数(9.81 m·s-2),θ为道路坡度夹角,A为汽车正面表面积(m2),ρ为空气密度(kg·m-3),Cd、Cr分别表示牵引力系数和滚动阻力系数,ε为车辆传动效率,η为发动机效率.
2 低碳木材物流网络优化建模
木材物流网络优化问题定义在完全连通图G=(N,A)上,其中N=H∪L∪P为节点集合,H为供材点集合,Si为供材点i∈H的供应量,L为备选木材物流中心集合.每个备选木材物流中心对应于一组确定的最大容量Vl、固定成本Bl、单位流转成本gl,以及固定碳排放量σ1l和单位碳排放σ2l.P为需材点集合,每个需材点的需材量为Nj,单位木材的粗加工成本为fpj,单位木材的粗加工碳排放为σ2j.A={(i,j)|i,j∈N,i≠j}为边集合.V为运材车辆集合,车辆k的车辆容量为Qk,在每条边对应的两点间的单趟行驶的成本和碳排放量分别为cijk和eijk.由于木材的供应点位于林区,而林区道路尤其是南方林区道路等级不高,道路宽度有限,存在道路坡度等,连接木材供应点和网络中其他节点的线路上的运输车辆的车型受到限制,只能选择较小的车型.如利用南方林区常用的六轮农用车进行供材点与其他节点的连接.而木材物流中心常选在交通较为便利的地点.而从木材物流中心发出的车辆则不受此限制,可以选择经济效益较高、环境影响较小的车辆完成从木材物流中心到需材点间的运输任务.故定义V=V1∪V2,V1、V2分别为从供材点和木材物流中心发出的车辆集合.在木材物流网络中,若木材采用中转的方式经木材物流中心转运,则在木材物流中心进行粗加工作业,定义φi为需材点i所需木材原料经粗加工作业后的失重率.
木材物流网络优化问题的决策对象包括木材物流中心的数量和位置,以及木材的流量流向.因此,木材物流网络优化模型包括三类决策变量,即选择备选木材物流中心l的0、1变量Zl,木材物流网络中节点i、j间的木材流量xij,以及车辆k在节点i、j间的运输次数wijk.
同时考虑成本目标和碳排放目标,构造木材物流网络多目标优化模型:
(6)
(7)

(8)
(9)

(10)
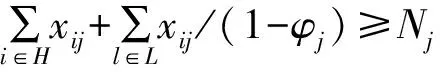
(11)

(12)
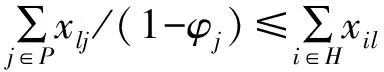
(13)
xij≥0 ∀i∈H,j∈L∪P
(14)
wijk≥0 ∀i∈H∪L,j∈L∪P,k∈V
(15)
Zl∈{0,1} ∀l∈L
(16)
式(6)表示木材物流网络总成本最小化,其中第1项表示车辆的运输成本,第2项表示木材物流中心固定成本,第3项表示木材物流中心变动成本.式(7)表示木材物流网络总碳排放最小化,其中第1项为木材物流中心的碳排放,第2项为需材点处的木材加工作业碳排放,第3项为运输碳排放.式(8)和式(9)分别约束了从供材点和木材物流中心发出的线路上木材流量与运材车辆任务次数的关系.式(10)和式(11)分别为供材点的供应量约束和需材点的需求满足约束.式(12)为木材物流中心的规模约束.式(13)保证了木材物流中心流出量小于流入量.式(14)~式(16)为变量约束.
依据对物流网络碳排放的不同测度范围,研究4种不同的木材物流网络碳排放测度范围(表1),可得出4种不同的木材物流网络优化模型[P1]~[P4],其中[P2]~[P4]的碳排放最小化目标函数分别如式(17)~式(19)所示.
(17)
(18)
(19)

表1 4个模型的碳排放测度方式Table 1 Carbon emissions measure methods of the four models
式中,Eijk为车辆k在节点i、j间单趟满载运输的碳排放.
3 实例分析
3.1 案例产生
选取福建省将乐县为研究区域,针对福建金森林业股份有限公司(简称金森公司)木材供应物流网络,进行实证研究.金森公司是福建省林业产业龙头企业和重要的国有林业采育场,主营业务包括森林培育营造和木材生产销售.
将乐县目前的木材物流模式是:木材在卖给一级批发商后进行砍伐,首先在楞场进行集中,再根据批发商对木材的销售情况进行分流.若购买者为大型森工企业,则将木材直接从楞场运往需求点;若购买者为二级批发商,则先将木材运送至二级批发商的木材货场,再由二级批发商进行销售后运送至木材需求企业.二级批发商的销售对象不仅包括小型需求企业,有时也包括大型木材企业.其中每阶段的木材运输则随机地由供需双方外包给第三方物流企业.该模式下木材物流的随机性较大,容易造成物流资源浪费严重的现象,也制约了木材物流服务水平的提高.如果将二级木材批发商看成木材需求点,则当前将乐县的木材物流模式为典型的直送模式;如果将二级批发商作为木材物流中心,则当前将乐县的木材物流模式为直送和中转模式并存的物流模式.但是就目前来说,二级木材批发商的规模较小,流向二级木材批发商的木材流量占总流量的比重不大.将乐县的木材物流现状也是当前南方林区的木材物流现状,因此选择将乐县金森公司作为本研究的应用案例具有代表性.
首先,基于区域内伐区各采伐点的木材年产量,在其3个分公司和1个子公司经营的22个伐区供材点选择其中7个年供应量超过1万m3的供材点作为供应点(该7个点2016年的总木材供应量为11.08万m3,占全公司总供应量的62.4%);其次,将公司的五大客户定为需求点;最后,使用GIS软件根据木材物流中心选址的基本约束条件(如满足用地规划、有足够的场地以及交通便利等)选出了4个备选木材物流中心(图2).
各节点间的连接由高速、省道、县道和乡村道路4种类型道路组成,通过初步计算可以得到供需点间的最短路径中各道路类型的长度,并获得对应的平均道路坡度、平均滚动阻力系数.南方林区从供材点出发的车辆通常为六轮农用车,故以典型车型风驰为例进行计算.从木材物流中心发出的车辆在案例中选用最常见的斯达-斯太尔ZJ6SL43U045木材运输车,相关参数如表2所示.
通常假设车辆行驶速度为定值[14],本研究综合考虑道路状况和运材车辆状况,将高速公路上运材车平均车速设为80 km·h-1,省道上运材车平均车速设为60 km·h-1,县道上运材车平均车速设为40 km·h-1,乡村道路上运材车平均车速设为30 km·h-1.高速公路平均滚动阻力系数为0.010,省道为0.010~0.018,县道为0.018~0.020,乡村道路为0.020~0.025.高速公路平均坡度为0,省道为0~0.5%,县道为0.5%~1.0%,乡村道路为1%~2%.最后,由于将乐县的年平均气温约为20 ℃,取ρ=1.205 kg·m-3.根据单位木材加工作业的碳排放按照标准[8],需材点单位木材加工作业的碳排放以1.153 1 kg·m-3为基准,各需材点具体单位木材加工作业碳排放取值根据规模效益确定,柴油的排放系数为74.1 kg·TJ-1[15].
3.2 木材物流网络碳排放测度
以福建金森林业股份有限公司在将乐县的木材供应物流网络为例,估算木材物流网络碳排放量,验证本文提出的木材物流网络碳排放测度方法.基于将乐县的木材物流现状,所有木材均为直送,以成本最小为目标进行木材调配,调运方案如图3所示,基于该调运方案进行将乐县木材物流网络的碳排放估算.
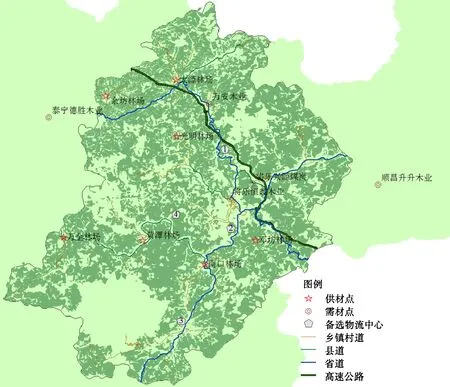
图2 将乐县木材物流网络示意图Fig.2 Timber logistics network in Jiangle County

表2 木材物流网络中的车辆的参数取值Table 2 Parameters value of vehicles in the timber logistics network
经计算,木材物流网络(图3)的碳排放为783.64 t,其中运输碳排放为694.72 t,占木材物流网络总碳排放的88.7%;木材加工碳排放为88.92 t,占11.3%;单位木材的运输碳排放为6.27 kg·m-3(木材的平均运距约为45 km),与文献[16]的运材碳排放的计算结果一致,在一定程度上表明本文采用的木材物流网络碳排放量估算方法的合理性.
3.3 木材物流网络优化中的碳排放
采用归一化约束方法[17]求得模型[P1]~[P4]的精确帕累托最优前沿,结果如图4所示.首先,4种模型的帕累托最优前沿形状和趋势大致相同;其次,[P1]和[P4]的帕累托最优前沿几乎呈现平移关系,由于[P4]用满载车辆的碳排放代替了运输车辆的实际碳排放,其帕累托最优前沿也处于坐标系中较[P1]稍高的位置,平均碳排放水平较[P1]高约2.7%;第三,[P2]和[P3]的帕累托最优前沿几乎重叠,因为在木材物流网络中,木材物流中心的固定碳排放十分微小,占总碳排放的比重小于3.5%;第四,[P2]的帕累托最优前沿可以近似为[P1]的向下平移,且平移的量较为明显,平均碳排放水平下降了约19.65%,这是因为在[P2]中未考虑节点的变动碳排放在木材物流网络总碳排放中占的比重(大于11.3%).

图3 将乐县区域木材物流调运方案Fig.3 Transportation plan of timber in Jiangle County

图4 4种模型的帕累托最优前沿示意图Fig.4 Illustration of Pareto optimal frontiers of the four models
因此,可以得出以下结论:(1)4种碳排放计算方式基本上都较清楚地表达了双目标低碳木材物流网络优化中碳排放目标和成本目标间的权衡关系;(2)木材物流中心的固定碳排放在木材物流网络总碳排放量中的比重十分微小,而加工碳排放(变动碳排放)在总碳排放量中占的比重较大;(3)在不考虑路径问题的物流网络优化中,是否区分车辆装载量的运输碳排放计算方法对实际碳排量估算的影响较小,几乎不影响模型优化解;(4)在考虑碳排放的区域木材物流网络优化问题时,为了简化计算,用线路(运输)碳排放代替网络碳排放量的估算方法具有一定的合理性.
4 讨论
在对物流网络碳排放测度方法的分析总结基础上,提出了木材物流网络碳排放测度方法,以福建省将乐县金森公司的木材物流网络为例进行了验证,通过与文献[23]研究结果相比较,验证了本文方法的合理性.此外,建立了同时考虑碳排放最小化和成本最小化的木材物流网络双目标优化模型,通过该模型分析了常见的物流网络碳排放测度方法对模型优化结果的影响.结果表明,不同碳排放测度方式下的帕累托最优前沿形状大致相同,但在坐标系中的位置不同.用车辆满载的碳排放代替实际运输车辆的碳排放会造成平均碳排放水平的略微上升,而忽略节点碳排放将造成平均碳排放水平的明显下降.

