基于改进遗传算法的大批量单面碎纸片拼接复原

中国电子科技集团公司第五十四研究所 杜 浩 刘雪峰

东北大学 蔡立晨

1.引言

碎纸片的拼接复原问题在历史文献修复、物证复原及情报获取等诸多领域都有着重要的应用。目前拼接复原工作大部分由传统的人工方式完成，但是在大批量碎纸片的情况下，人工拼接将变得十分缓慢并且低效。在计算机视觉极大发展的今天，采用计算机技术，运用机器视觉的原理对碎纸片进行拼接复原的方法应运而生。

2.模型假设与分析

再进行算法设计之前，本文对问题做出如下假设：假设碎片无噪声污染；各个碎片之间相互关联；同时假设文件中文字的行间距确定；没有两个相同的碎纸片并且不涉及手写稿。

对于仅有纵向切割或者横向切割的情况，各个碎纸片的边界信息丰富，可以通过使用边缘像素值作为特征进行匹配。在横向切割和纵向切割的影响下，碎纸片包含信息更少，本文首先采用积分投影的方式进行按行分类，并设计的基因融合算法，针对大批量的碎片匹配效率低下的问题，在遗传算法的迭代过程中融合个体，能在很大一定程度上保留最优的匹配，极大程度加速了算法的收敛，可以很好地解决大批量碎纸片匹配效率低下的问题。

3.算法设计

符号约定：

图像的水平积分投影特征以及边缘特征：

3.1 特征提取

在仅纵向切割或者仅横向切割的情况下，本文提取边缘像素特征。以纵向切割为例，相邻的碎片相似程度高，左右边缘可拼接在一起形成完整的文字。如果被拼接的两个碎纸片不相邻，那么其拼接之后的边缘不能形成完整的文字，相似程度较低。本文对比不同碎纸片特征之间的余弦距离以得到最优匹配[1]。

在双向切割的情况下，本文首先进行按行分类。横切和纵切的影响下，碎纸片所包含的文本信息变少，使得拼接难度增大。由于文字字高不一致，直接按行分类难度大。在进行水平积分投影之后可减少字高不一致带来的影响。本文首先对碎纸片提取到的水平积分投影特征进行了二值化，进一步减少字高不一致带来的影响。按行分类如图1(a)所示：

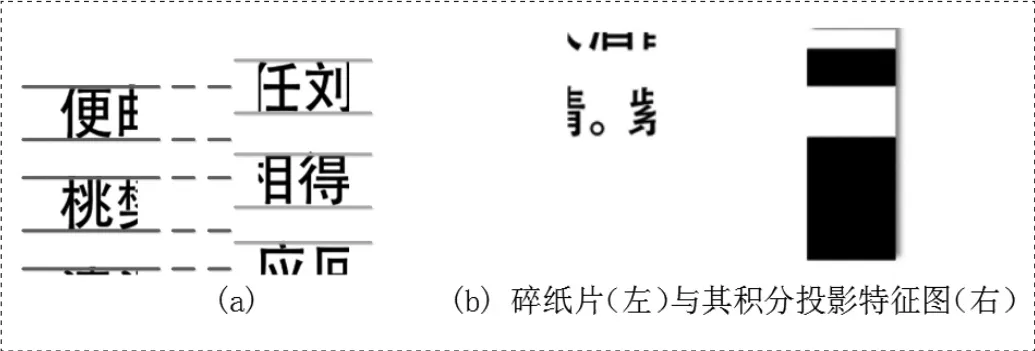
图1

3.2 余弦距离

余弦距离通过计算两个向量夹角的余弦值来评估其相似程度[2]。假设：

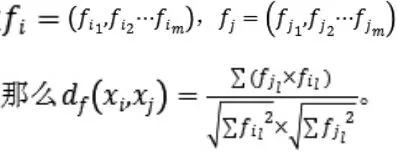
本文通过计算特征之间的余弦相似度度量碎纸片之间的匹配程度。

3.3 基于基因融合改进的遗传算法

遗传算法是一种模拟生物界自然进化过程来解决最优问题的算法，该算法在求解问题的基本步骤为：建立表示可行解的基因编码；种群初始化；计算适应度函数；对个体进行选择、交叉和变异操作；终止条件判断[3]。

本文设计的遗传算法中，每个个体代表一种碎纸片的排列组合方式，每个个体的适应程度，由其排列方式决定。不妨假设当前的切割方式为仅纵切，种群中的某一个个体代表一种碎纸片的排列方式，即，那么对于当前的排列方式便可以计算得到当前个体的适应度值。种群的初始化由蒙特卡洛方法生成[4]，选择方式由赌轮盘形式生成。

传统的遗传算法中的交叉运算在一定程度上会破坏优秀基因的组合。本文针对大批量碎纸片图像匹配效率低下的问题，提出了基因融合的操作。在计算个体适应度的同时，能得到当前组合下的相互邻接的碎纸片的匹配程度，由余弦距离得出。当两个碎纸片真正相邻时，其匹配程度较大，本文利用基因融合的方式将此两者标记为不可分，即每次操作的过程中两者将作为一个整体存在。终止条件是所有基因融合完毕，即每个碎纸片都找到与之相邻的最佳匹配。其过程示意图如图二所示：

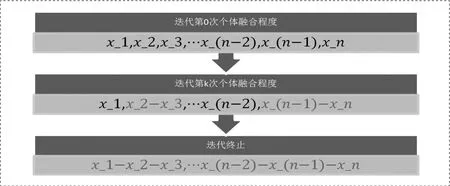
图二 （红色并且加入连接符的表示被融合的基因）

4.实验结果与分析

实验在MATLAB平台上进行，结果如图三所示：

图三 实验结果

实验结果表明本文所提出的基于基因融合的遗传算法效果稳定，在实验过程中可明显的具有更快的速度。

5.结语

本文建立了一种基于基因融合的改进遗传算法对碎纸片进行拼接复原，通过实验取得了较好的结果。但是实验过程中仍然存在诸多问题，需要更高的精度以及更加稳定的特征提取方式。