龙开口水电站坝基防渗墙数值模拟

梁 岩，毛瑞敏，王 毅，罗小勇

(1.郑州大学 土木工程学院，河南 郑州 450001；2.华能澜沧江水电开发有限公司，云南 昆明 650214；3.中南大学 土木工程学院，湖南 长沙 410075)

防渗墙是一种修建在松散透水层或土石坝(堰)中起防渗作用的地连续墙[1]。防渗墙技术源于20世纪50年代的欧洲，因其结构可靠、防渗效果好、适应各类地层条件、施工简便以及造价低等优点[2-3]，尤其是在处理坝基渗漏、坝后流土、管涌等渗透变形隐患问题上效果良好，在国内外得到了广泛应用[4-9]。防渗墙施工监测是防渗墙施工的重要组成部分[10]。根据防渗墙施工监测与数值模拟的对比分析对误差进行预测调整，不仅可以避免施工事故，还可以使防渗墙最大限度地接近理论状态[11-14]。

我国水利水电工程中有防渗要求的建筑物一般首选防渗墙，经过多年的应用与创新，防渗墙技术已经相当成熟，但研究主要集中在防渗墙结构特性与施工方面，对防渗墙施工监测方面的研究较少[15-20]。本文以龙开口水电站坝基深槽开挖工程为依托，采用有限元方法确定砂卵石地基土体对防渗墙支承刚度系数的合理取值，建立防渗墙支护结构与土体相互作用的有限元模型，分析施工过程中墙体的可靠性，并对施工期间防渗墙的变形进行实时监测。防渗墙的实时监测有利于避免施工事故的发生，保证防渗墙施工期间的安全。

1 工程概况

图1 单层人字形防渗墙方案(单位：cm)Fig.1 Monolayer herringbone underground wall for retaining water (unit: cm)

龙开口水电站坝基施工过程中，在河床坝基处发现1条内部填满砂卵石的深槽，深槽宽约20 m，覆盖层厚度达30 m，且沿顺河向延伸穿越水电站大坝基础。如果不对深槽进行加固防渗处理，会严重影响龙开口水电站坝基的施工质量，结合实际工程情况，在坝基深槽处设置1道人字形防渗墙(见图1)。

防渗墙为钢筋混凝土结构，厚1.2 m，高24.5 m,最大宽度24.0 m，开挖高程1 186.5～1 162.0 m。为保证深槽开挖过程中防渗墙的结构稳定性，在防渗墙后设置一定的撑梁支护，并采用分层开挖与边开挖边支护的开挖方式。深槽内砂卵砾石层共分6层进行开挖，各层开挖厚度分别为6.5,4.0,4.0,4.0,3.0,3.0 m，开挖过程共浇筑4道支撑梁：第1道支撑梁(EL.1 180～1 184 m)；第2道支撑梁(EL.1 176～1 180 m)；第3道支撑梁(EL.1 172～1 176 m)；第4道支撑梁(EL.1 168～1 172 m)。

2 支承刚度系数的确定

采用Midas有限元分析软件，选用四节点薄板单元模拟钢筋混凝土防渗墙墙体，八节点六面体实体单元建立复杂的砂卵石地基土体非线性弹性模型。根据地基资料，取砂土黏聚力c=0，内摩擦角32°，土体按照非线性材料考虑。约束土体两侧面及底面节点X，Z轴的平移自由度和绕X，Y，Z轴的转动自由度，在土体后方的面内节点上沿Y轴施加一般支承约束，土体前面的节点沿Y轴负方向设置只受压的节点弹性支承约束，支承刚度设置为109kN/m，土体顶面无约束。

防渗墙发生单位位移时，单位面积地基土的反力即为土体的支承刚度系数。为了确定防渗墙后土体的支承刚度系数，先对砂卵石地基发生单位位移的情况进行有限元模拟，使地基土体单元的节点发生单位位移，计算节点反力，从而确定支承刚度系数。

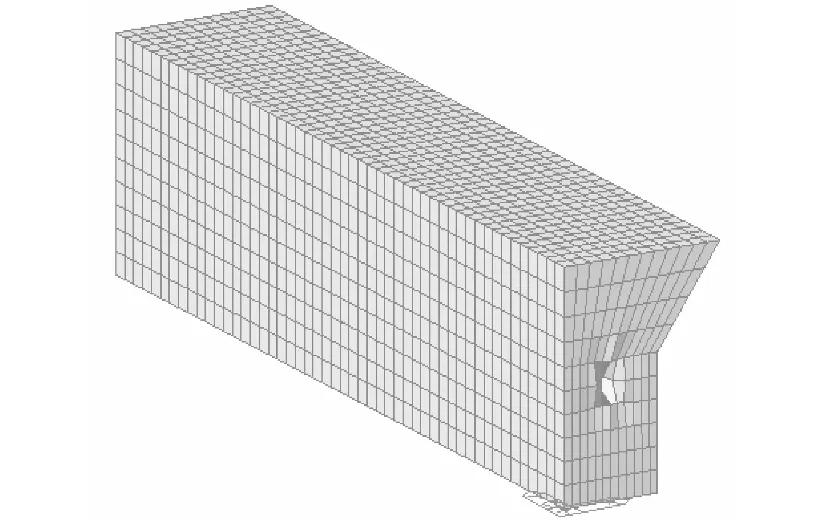
图2 支撑刚度系数计算模型Fig.2 Support stiffness coefficient calculation model

图3 施加强制位移节点布置Fig.3 Layout of forced displacement node

防渗墙后土体主要为漂石砂卵砾石层，根据现场测试，压缩模量Es为0.035 ～0.400 GPa。考虑到土体界面与岩石界面的接触形式介于刚性连接和滑动支承之间，分别选取Es=0.035和0.400 GPa，土体界面与岩石界面分别用刚性连接和滑动支撑模拟建立了4种有限元分析模型，模型1(刚性连接)和模型2(滑动支撑)的压缩模量Es为0.035 GPa；模型3(刚性连接)和模型4(滑动支撑)的压缩模量Es为0.400 GPa。

支撑刚度系数计算模型如图2所示，砂卵石地基土采用实体单元模拟。在模型的XOZ平面内选取适当的节点沿Y轴正方向施加1 mm的强制位移以求解砂卵石地基的支承刚度系数，灰色区域为施加强制位移位置的变形。考虑到节点所受约束的强度会随其与边界距离的不同而发生变化，在XOZ平面内的同一深度，分别选取关键截面上的67，68，70，72，74，76和77号节点作为强制位移的施加位置(如图3所示)。在4种模型中分别在上述节点沿Y轴正方向施加1 mm节点强制位移。

同一深度，强制位移作用节点沿X轴方向变化时，节点上Y方向反力如表1所示。

综合分析上述4种模型的计算结果，可知防渗墙与砂卵石地基土体之间的接触形式更接近于滑动支撑连接，压缩模量取值越大，土体刚度系数也越大。砂卵石河床地基土体的支承刚度系数计算值都在35 kN/mm左右，土体上表面支撑刚度系数约为18 kN/mm，边界处根据岩石支撑刚度范围支承刚度系数为32～44 kN/mm。

表1 不同模型中各节点Y方向的反力Tab.1 Reacting forces of nodes of different models in Y aixs direction kN

3 不同支撑条件下防渗墙可靠性分析

为分析支承条件变化对防渗墙可靠性分析的影响，选取防渗墙上游水位为1 195 m，砂砾石层开挖至1 176 m时，建立不同的支承刚度系数有限元模型，通过对比各模型防渗墙的位移与内力，分析支承刚度系数变化对防渗墙可靠性分析的影响。

模型A：选取35 kN/mm作为防渗墙后土体支承刚度系数，不考虑不同土体支承刚度系数取值对防渗墙可靠性分析的影响。

模型B：土体上表面取支承刚度系数为18 kN/mm；距左右两侧面边界0～1.5 m范围内取支承刚度系数为44 kN/mm，1.5～4.0 m范围内取支承刚度系数为38 kN/mm；其余部分取为35 kN/mm。

模型C：土体上表面取支承刚度系数为18 kN/mm；距左右两侧面边界0～1.5 m范围内取支承刚度系数为32 kN/mm，其余部分取支承刚度系数为35 kN/mm。

防渗墙底部嵌入岩体，顶部与大坝浇筑成整体，周边为岩石，故在防渗墙有限元模型中将防渗墙上下端视为固定端，左右视为简支。模型计算简图和防渗墙有限元模型如图4和5所示，图中H1为开挖及地基加固均已完成的高度,H2为防渗墙开挖地基尚未加固高度，1 186.5和1 162.0 m为深槽开挖的高程。考虑砂砾石地基的弹性支承作用，在H1以上范围内取弹簧刚度为60 000 kN/m的弹性支座，在H1以下范围内取弹簧刚度为30 000 kN/m的弹性支座。

图4 模型计算Fig.4 Simplified calculation model

图5 防渗墙有限元模型Fig.5 Finite element model for impermeable wall

3.1 位移变化

各模型的位移立面图和位移侧视图见图6。

图6 各模型位移Fig.6 Displacements calculated by models

模型A，B，C计算得出的防渗墙最大位移分别为3.52，3.28和3.33 mm。与模型A相比，模型B,C仅分别减小7.1%和5.6%。

3.2 内力变化

模型A，B，C中防渗墙的内力计算结果见图7～9。

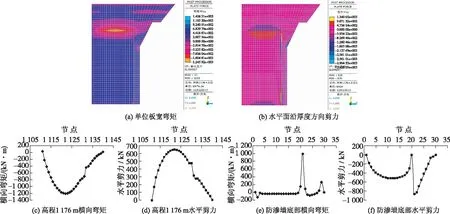
图7 模型A中防渗墙内力Fig.7 Internal force of underground wall for retaining water in model A

由图7可见，模型A中防渗墙所受负弯矩在防渗墙中上部局部达到最大值-1 245.9 kN·m；正弯矩在防渗墙底部支座处达到最大值1 406.3 kN·m；20，21，22为防渗墙折角局部节点，该处受力复杂，弯矩与剪力较大，水平剪力值为3 428.1 kN ，其余部位最大剪力为1 260.5 kN；防渗墙承载力满足设计要求。

图8 模型B中防渗墙的内力Fig.8 Internal force of underground wall for retaining water in model B

由图8可见，模型B中防渗墙所受负弯矩在防渗墙中上部局部达到最大值-1 307.1 kN·m；正弯矩在防渗墙底部支座处达到最大值1 222.8 kN·m；20,21,22为防渗墙折角局部节点，该处受力复杂，弯矩与剪力较大，水平剪力值为3 341.4 kN，其余部位最大剪力为875.7 kN；防渗墙承载力满足设计要求。

图9 模型C中防渗墙的内力Fig.9 Internal force of underground wall for retaining water in model C

由图9可见，模型C中防渗墙所受负弯矩在防渗墙中上部局部达到最大，为-1 233.6 kN·m；正弯矩在防渗墙底部支座处达到最大，为1 338.1 kN·m；20,21,22为防渗墙折角局部节点，该处受力复杂，弯矩与剪力较大，水平剪力值为3 383.1 kN；防渗墙承载力满足设计要求。

弯矩剪力都相对较大的变宽中部位置处在3种模型中计算得出的内力值分别为：模型A，弯矩-1 077.9 kN·m，剪力590.6 kN；模型B，弯矩-1 059.9 kN·m，剪力585.0 kN；模型C，弯矩-1 068.8 kN·m，剪力588.3 kN。可见，模型B和C与模型A相比，弯矩减小约1.7%和0.8%；剪力减小约0.9%和0.4%。

综上所述，单位板宽最大负弯矩位于防渗墙中上部，最大正弯矩位于防渗墙底部，最大剪力位于防渗墙中部折角处。模型A的内力计算结果偏大，说明土体支承刚度系数取值偏于安全，可满足计算要求。

4 施工过程中监测结果验证

为监测深槽下游第1道防渗墙的变形，研究深槽开挖对防渗墙安全性能的影响，在6#，7#以及8#槽段共布置了6个测斜孔。上游防渗墙内6个测斜孔孔口高程均为1 194.5 m。测斜仪均采用钻孔方式埋设，具体埋设方式如下：首先在防渗墙内钻孔或在墙体内起拔钢管形成预留孔，然后将测斜仪安置在孔内。由于孔深较大时不易保证钻孔垂直，采用墙体内预留孔的方法埋设测斜仪，直径为146～163 mm的厚壁无缝钢管。

深槽防渗墙下游面第1层(EL.1 184～1 180 m)开挖完成后在防渗墙下游面形成临空面的同时，防渗墙上游面正在进行固结灌浆施工。根据监测结果，7#槽段两个测斜孔的实测位移变化量均有不同程度的增加，其中以孔深较深的IN7-2变化量最大，在EL.1 180.5 m高程处累计变形量高达5.82 mm，开挖前后最大变形量差为5.36 mm。

根据施工监测过程中测斜仪观测的数据，IN7-2测斜孔在各高程处的变形量变化曲线如图10所示。

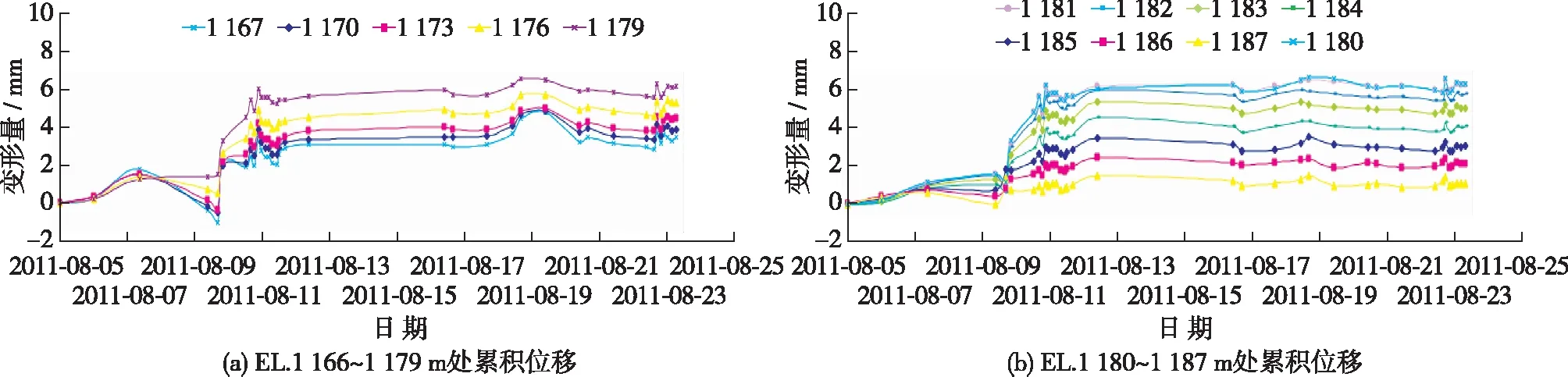
图10 IN7-2倾斜仪在防渗墙EL.1 166 m～1 187 m处测得的累积位移Fig.10 Measured cumulative displacement by IN7-2 inclinometer at EL.1 166-1 187 m of underground wall for retaining water

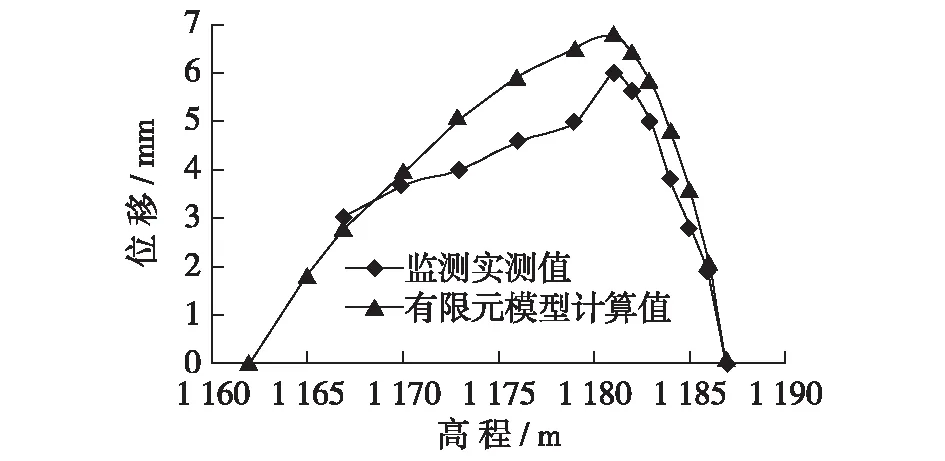
图11 防渗墙变形对比Fig.11 Comparison of deformations of underground wall for retaining water

由图10可知，防渗墙变形主要是从上游面向下游面的变形，这是由下游砂卵砾石层的开挖形成临空面及上游固结灌浆双重作用引起的。根据上述分析结果，为避免变形量继续增加，立即停止上游面灌浆作业，并随即展开下游面支撑梁施工作业。

从图10中可见，上游面灌浆停止后，防渗墙变形量基本稳定在5 mm左右，最大达6 mm，监测结果证实上述分析正确。在浇筑第1层支撑梁混凝土以后，防渗墙变形量逐渐减小，最后约3 mm。根据防渗墙有限元分析参数确定方法，模拟前期施工过程，通过对比有限元模型A计算值与施工监测实测值(见图11)可知：有限元模型计算结果与实测值接近，理论计算结果略大，但可作为实际施工及监测参考。

模拟后续施工过程，并指导后续各层开挖。在防渗墙下游面3层砂卵砾石层的开挖及支护过程中，第1层开挖过程中防渗墙的变形量较大，其主要是由上游面固结灌浆和下游面开挖产生临空面共同引起。下游面支护完成之后，防渗墙变形受到抑制。第2层及第3层开挖过程中防渗墙未发生较大变形。由此可见，开挖-支护-开挖的施工模式较好地抑制了防渗墙变形，保证了防渗墙施工安全和施工质量。

5 结 语

(1)防渗墙与砂卵石地基土体之间的接触形式接近于滑动支撑连接，压缩模量取值越大，土体支撑刚度系数也越大。

(2)不同支撑条件下，防渗墙位移变化比内力变化大，支撑条件对墙体变形影响较大。总体上，防渗墙单位板宽最大负弯矩位于防渗墙中上部，最大正弯矩位于防渗墙底部支座处，最大剪力位于防渗墙中部折角处。

(3)通过建立不同支撑条件的防渗墙有限元模型，获取合理的支承刚度系数，为龙开口水电站深槽施工监测提供了可靠的理论监测依据。