大支承力径向电磁轴承结构设计及试验研究
任正义, 李乃安
(1.工程训练国家级试验示范中心(哈尔滨工程大学),哈尔滨 150001;2.哈电集团哈尔滨电站阀门有限公司,哈尔滨 150060)
传统8磁极径向电磁轴承的磁极线槽采用等面积设计法,在重载、高转速工况时,磁极结构会因体积的增大而使磁极间的间隙变大,导致整个磁场分布不均匀[1]。为了改进传统8磁极径向电磁轴承的上述缺陷,充分利用定子空间,设计了E形结构的12磁极径向电磁轴承,其优点是2个小磁极对转子产生的水平方向的分力相互抵消,减小了x和y方向上的相互耦合[2]。
1 径向电磁轴承的结构设计
设计的E形结构12磁极径向电磁轴承结构如图1所示。

图1 12磁极径向电磁轴承结构
1.1 支承力计算
当转子位于平衡位置时(图2),根据安培环路定理(Ampere circuital theorem)[3]可得

图2 径向电磁轴承的差动控制示意图
(1)
则磁感应强度为
(2)
由Maxwell磁力公式求得大磁极与转子间产生的电磁力为
(3)
式中:y0为理想单边气隙;μ0为空气磁导率;N为大磁极线圈匝数;i0为偏置电流;S0为大磁极有效截面面积。
同理,当转子处于平衡位置时,小磁极与转子间产生的电磁力为
(4)
式中:S1为小磁极有效截面面积,S1=S0/2。
已知大磁极与小磁极中心线间的夹角为α,则一个磁极组在y方向上产生的电磁力为
(5)
当转子在y方向产生向下的微小偏移量Δy时,由于电磁轴承的工作方式为差动控制,假设通过控制器输出的控制电流为Δi,则上磁极组输入的工作电流为i0+Δi,下磁极组输入的工作电流为i0-Δi,则上、下磁极组产生的电磁力分别为
(6)
(7)
则径向电磁轴承在y方向上产生的电磁合力为
(8)
在工作点(Δy=0,Δi=0)附近将(8)式进行Taylor展开并忽略高阶次项,非线性电磁力可以近似简化为线性电磁力模型,即
Fy≅kyΔy+kiΔi,
(9)
(1+cosα),
(10)
(1+cosα),
(11)
式中:ky为12磁极径向电磁轴承的位移刚度系数,与位移的改变量有关;ki为12磁极径向电磁轴承的电流刚度系数,与电流的改变量有关。而且规定y的正方向磁极为磁极A,x正方向磁极为磁极B,y负方向磁极为磁极C,x负方向磁极为磁极D。
1.2 主要结构参数
设计的12磁极径向电磁轴承主要结构尺寸如图3所示,各参数设计计算如下。

图3 12磁极径向电磁轴承结构参数
1.2.1 大、小磁极宽度L0,L1
已知定子高度Hd,根据(11)式推出定子大、小磁极宽度分别为
(12)
(13)
式中:μ0=4π×10-7;硅钢片叠片率Kl=0.97;夹角α=33.75°。
1.2.2 定子、转子磁轭宽度C1,C2
为了尽可能减少定子、转子磁轭处产生的磁漏,要求定子、转子磁轭宽度一定不能小于定子小磁极的宽度,一般取值为
(14)
1.2.3 绕组匝数N
当通入线圈中的电流达到最大时,在磁路中能够激励出最大磁通密度,这时铁磁材料的性能可以发挥到最佳,可以得到最大的许用安匝数。线圈的安匝数与磁感应强度之间的关系为[3-5]
(15)
则大、小磁极绕组匝数分别为
(16)
(17)
1.2.4 绕组线径dc
线圈导线中的最大许用电流决定了绕组的线径,最大电流与绕组线径dc之间的关系为
(18)
则绕组裸线线径为
(19)
式中:ε0为电流密度,取值为3~5 A/mm2。
1.2.5 定子内经D0
D0=d+2y0,
(20)
式中:d为转子外径。
1.2.6 磁极高度h
由图3几何关系可知,磁极间距t0,t2满足关系式
(21)
则磁极间距为
(22)

(23)
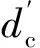
再由小磁极绕组匝数N1得小磁极绕组的单层匝数为
(24)
则小磁极绕组线圈的高度为
(25)
式中:Ncd为小磁极绕组线圈的单层匝数;lcd为小磁极绕组线圈的高度。
同样保留20%的裕度,则磁极高度为
(26)
1.2.7 定子中径D1
D1=D0+2h。
(27)
1.2.8 定子外径D2
D2=D1+2C1。
(28)
1.2.9 结构参数
由上述公式取整计算,最终得出径向电磁轴承结构参数见表1。根据设计出的结构参数加工出径向电磁轴承实物如图4所示,其中定子绕组呈现为注入环氧树脂以后的饱和状态,螺纹孔为吊装及后续试验所用。

表1 径向电磁轴承结构参数

图4 径向电磁轴承实物图
2 径向电磁轴承磁场有限元分析
通过Solidworks三维制图软件对径向电磁轴承进行结构建模,模型主要包括定子以及线圈,再将建好的模型保存成*.sat格式导入到Maxwell 3D Design中转换为2D模型[6-8]。为模型中的各个部分添加材料属性,其中定子材料为电工纯铁,转子材料为42CrMo,设置空气的相对磁导率为1.0;然后加载边界条件和激励,磁极绕组的匝数为160,绕组中加载偏置电流分别为5,10 A时,计算求解并查看结果,分析此时径向电磁轴承的磁场分布情况以及磁感应强度的变化情况。
加载偏置电流为5 A时的磁场分布、气隙处的磁感应强度变化曲线如图5所示。由图5a可以看出,在定子内、外环以及定子之间形成稳定的磁场,磁力线分布均匀;磁场主要分布在内、外环磁极面处以及线槽四周,并且在径向电磁轴承靠近线圈槽处达到最大值。当线圈中加载5 A的偏置电流时,气隙处的磁感应强度可以达0.56 T以上(图5b)。
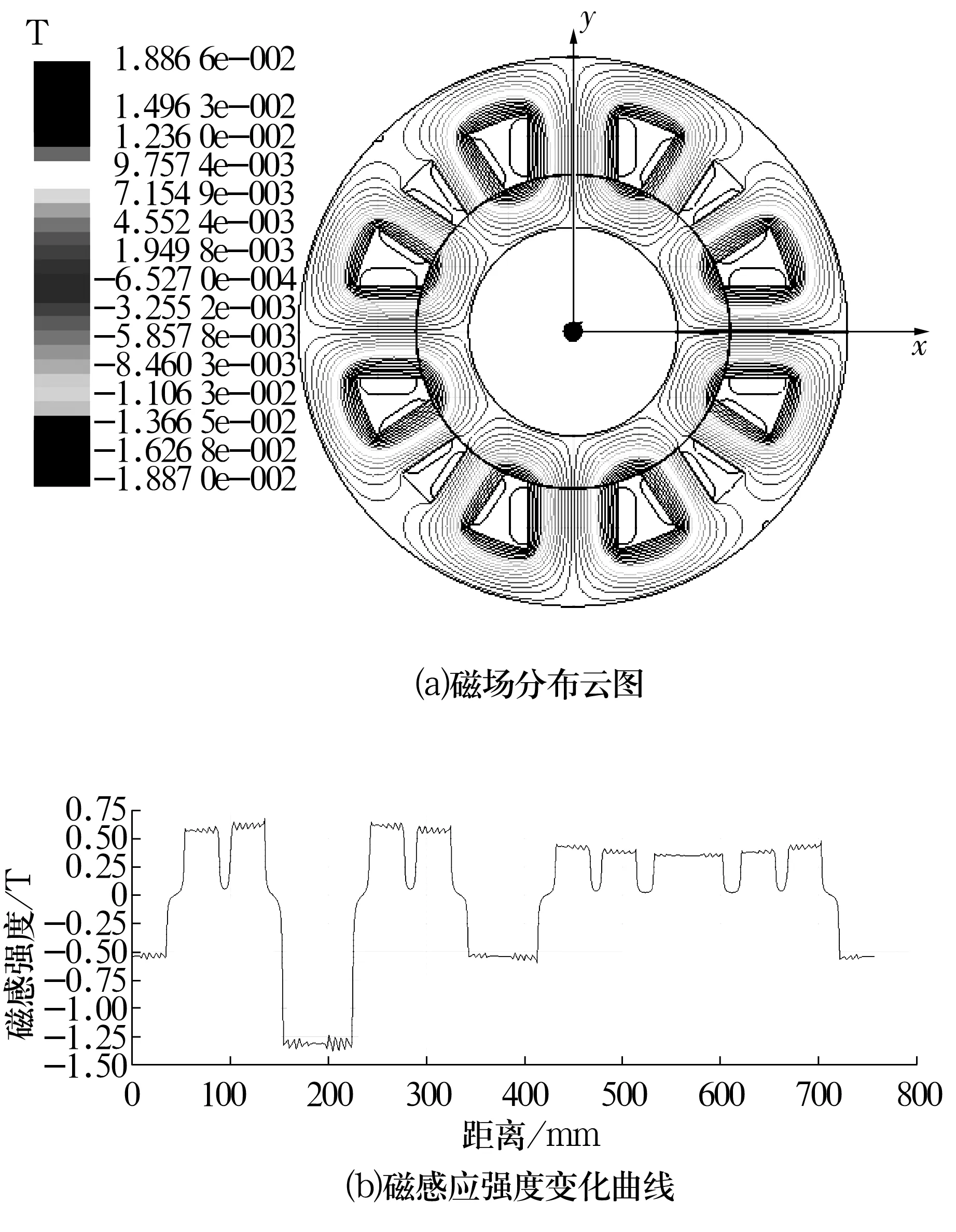
图5 偏置电流5 A下的磁场分布和气隙处的磁感应强度
偏置电流为10 A时的磁场分布、气隙处的磁感应强度变化曲线如图6所示。对比偏置电流为5 A时的磁场分布,虽然电流增加1倍,磁场并没有随着电流的增加而紊乱,磁场分布均匀,并且磁力线更为密集;定子内、外环气隙处的磁感应强度由0.56 T增加到1.2 T,说明能够提供大支承力。
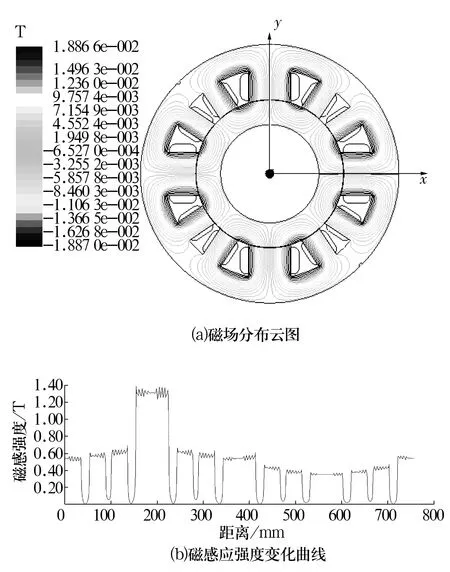
图6 偏置电流10 A下的磁场分布和气隙处的磁感应强度
3 径向电磁轴承支承性能验证
考虑到V形槽的定心性较好,且方便用线切割加工,因此,采用V形槽作为径向电磁轴承的固定支承座,通过钢条折弧将径向电磁轴承固定于V形槽上,以便电磁轴承定子在承受转子给的反作用力时不被吸起,试验台如图7所示。试验参数见表2。

图7 径向电磁轴承试验台实物图

表2 系统试验环境
试验测试采用250 kg级BSS传感器4个(输出电压0~10 V)和NI公司的数据采集系统(PXI),具体见表3。

表3 数据采集系统
测试完成后,将采集到的数据进行整理,并通过软件绘制成径向电磁轴承的电磁特性曲线,结果如图8所示。
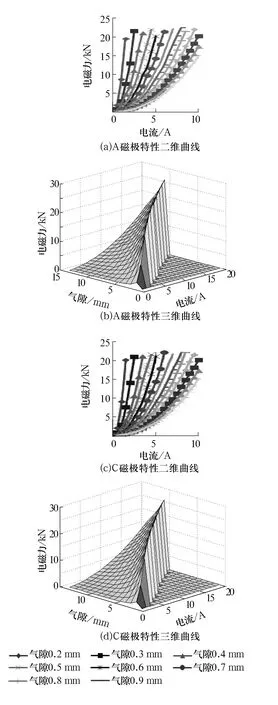
图8 径向电磁轴承的电磁特性曲线
从图中可以看出,对于每一条气隙恒定的曲线,随着电流的增大,径向电磁力也随之增加且增长幅度越来越大。当取一恒定电流值比较时可以发现,随着气隙的增大,电磁力逐渐减小且减小的幅值越来越小。
通过现场转子稳定悬浮效果来看,当单边气隙大于0.7 mm、偏置电流小于4 A时,曲线的线性度变差,这导致径向轴承动态特性显著恶化;当单边气隙小于0.3 mm时,电磁特性曲线非常的陡峭,这导致很小的外界干扰就可能产生很大的电磁力,即系统的稳定性变差。
4 结束语
以最大承载力为目标,设计了12磁极径向电磁轴承结构,对磁场分布进行分析,并进行了支承性能试验,验证了设计的正确性。得到了为保证电磁轴承的稳定性和动态特性,稳定悬浮位置的单边气隙应该为0.3~0.7 mm,如果单边气隙超过0.7 mm,则偏置电流应大于4 A。为今后大支承力径向电磁轴承的设计提供了参考。

