采用标准V形定位块测量圆锥滚子圆锥角

高武正，方芳，刘旗，王梦茵

(1.洛阳轴承研究所有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039；3.滚动轴承产业技术创新战略联盟，河南 洛阳 471039)

圆锥滚子轴承广泛应用于轨道交通行业中，圆锥滚子是圆锥滚子轴承的重要组成零件，其圆锥表面径向对应的2条素线之间的夹角(简称圆锥角)的正确与否影响整套轴承的装配、旋转稳定性以及承载后与内外圈工作面的接触程度，进而影响整套轴承的承载力与使用寿命。实际加工中，多采用轴承专用仪器D744通过与标准滚子的比较进行测量。

1 专用定位块检测

传统检测方法如图1所示，采用专用定位块来测量圆锥角，滚子被放置在水平检测台上，滚子侧面放置一块等于滚子半角的角度块，滚子放置后外径下素线与底部测台(测量基准)重合，上素线保持水平，通过正弦仪测得上素线与底部测台的夹角2α′，即圆锥滚子的圆锥角2α[1-3]。此种方法的关键在于侧面的角度块，如果角度块的角度不准确，下素线与底部测台的重合度不高，则会造成一定的测量误差，导致测量精度不高。

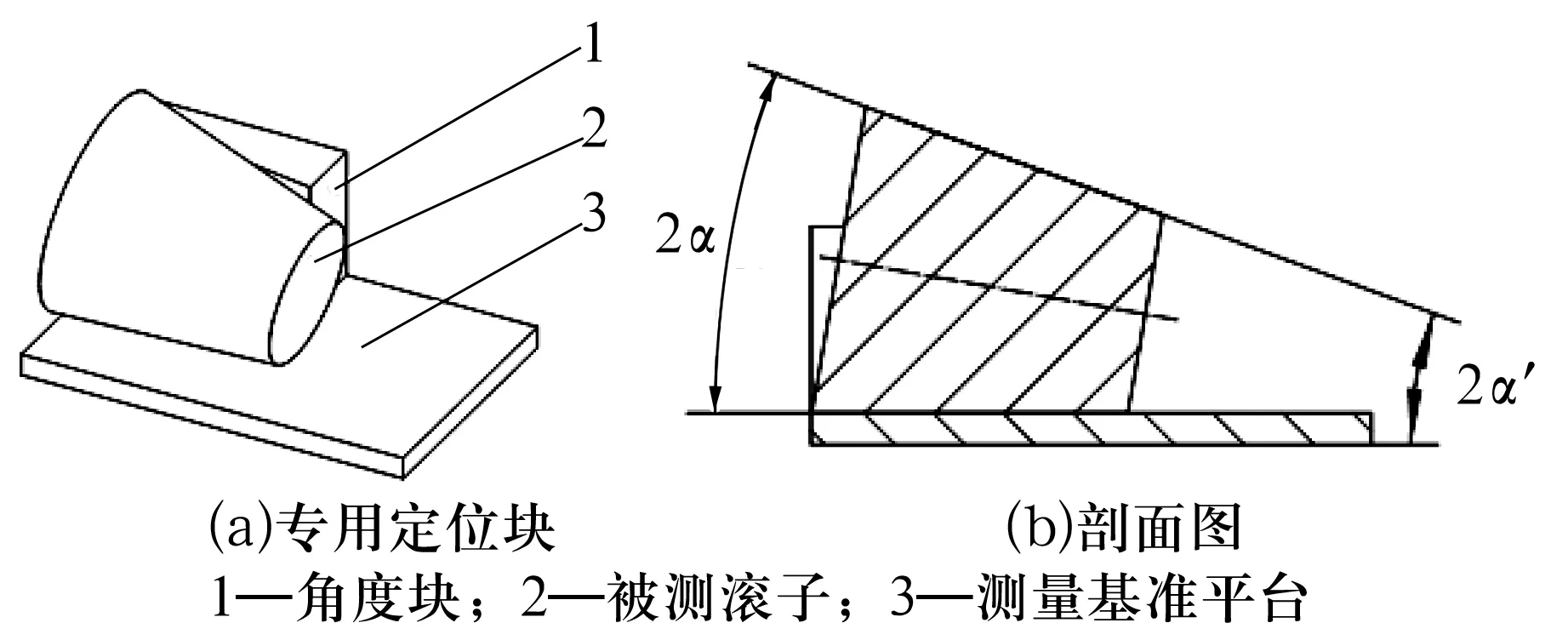
图1 传统专用定位块检测圆锥角示意图

2 标准V形定位块检测

由于传统检测方法需要准备与滚子角度匹配的高精度的角度块，对于临时检测很不方便，而轮廓仪的精度越来越高，因此，尝试采用轮廓仪通过标准V形定位块直接测量圆锥滚子的圆锥角，更加便捷地应用于生产中。

采用标准120°V形定位块检测圆锥角的示意图如图2所示，根据剖面图可以清晰观察到圆锥滚子的下素线与V形定位块底部测量基准并不重合，若测得上素线与测量平台的基准夹角为2α′,下素线与测量平台的夹角为δ，则实际的圆锥角为

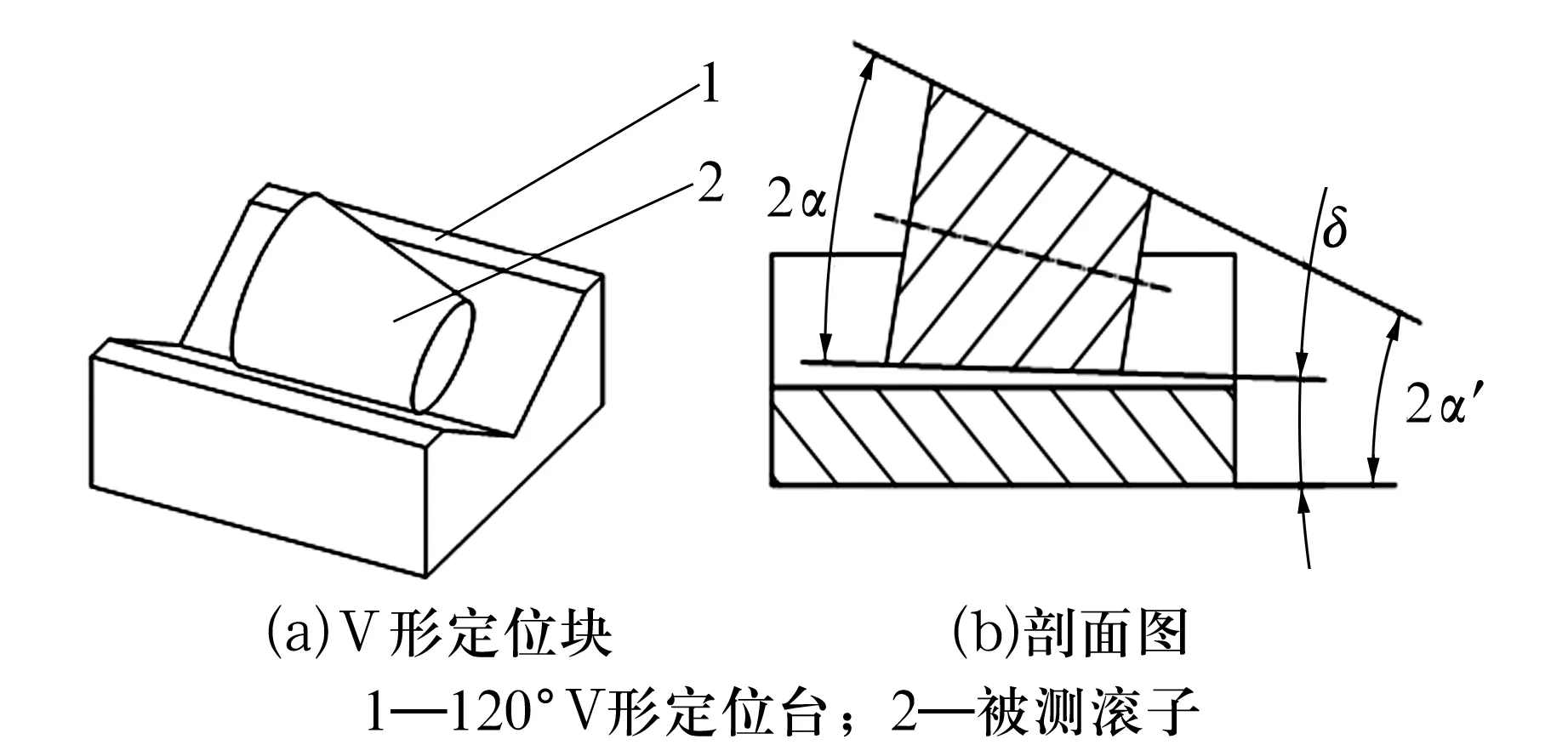
图2 标准120°V形定位块检测滚子角度示意图

2α=2α′-δ。

(1)

3 测量精度分析

3.1 各参数对误差角δ的影响

采用SOLIDWORKS2014三维软件对滚子与V形工作台建模，并添加滚子外径面与2个V形定位面相切约束，然后使用垂直底部测量平面并通过滚子轴线平面做剖面，通过SOLIDWORKS测量工具可以得出图2所示的2α′及δ，通过变换滚子大端直径、滚子角度、V形定位块角度得到不同的误差角δ见表1—表3。

表1 滚子大端直径对误差角δ的影响

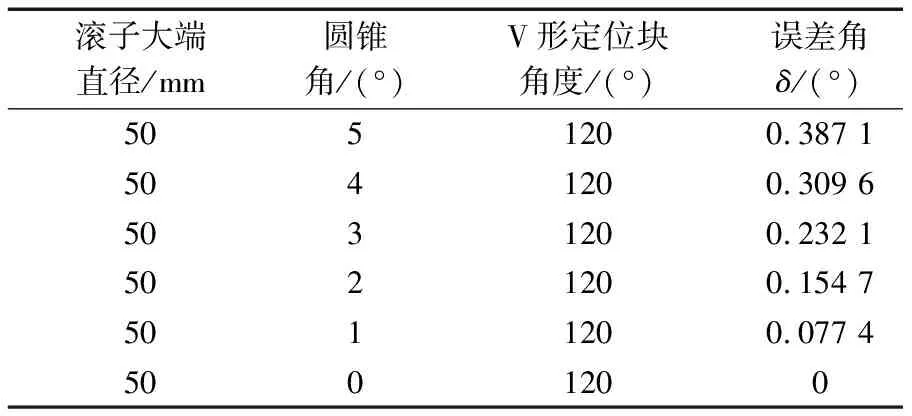
表2 圆锥角对误差角δ的影响

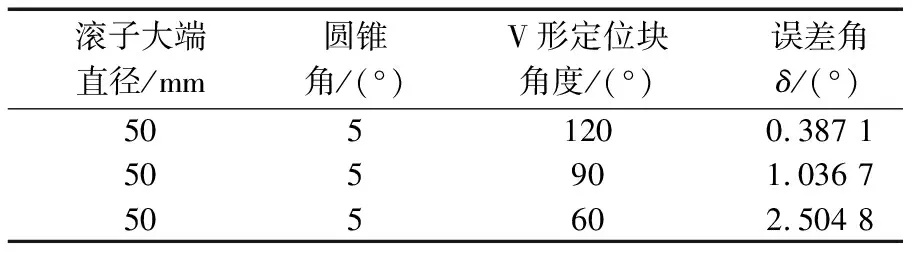
表3 V形定位块角度对误差角δ的影响

由表中数据可得：圆锥滚子在标准V形定位块上定位后，下素线与底部测量基准误差角δ有以下变化规律：

1)δ不随圆锥滚子大端直径变化而变化；

2)δ随圆锥角变大而变大；

3)δ随V形定位块角度变小而变大。

3.2 误差角δ与圆锥角的回归分析

为确定误差角δ与圆锥角之间的关系，选取生产中最常用的120°V形定位块，圆锥角选择0°～5°，每隔0.5°得到一个误差角δ，通过Excel表格散点图及其自带的回归分析功能得到如图3所示的线性回归图，将回归方程进行转化得误差角δ与圆锥角2α的关系式为

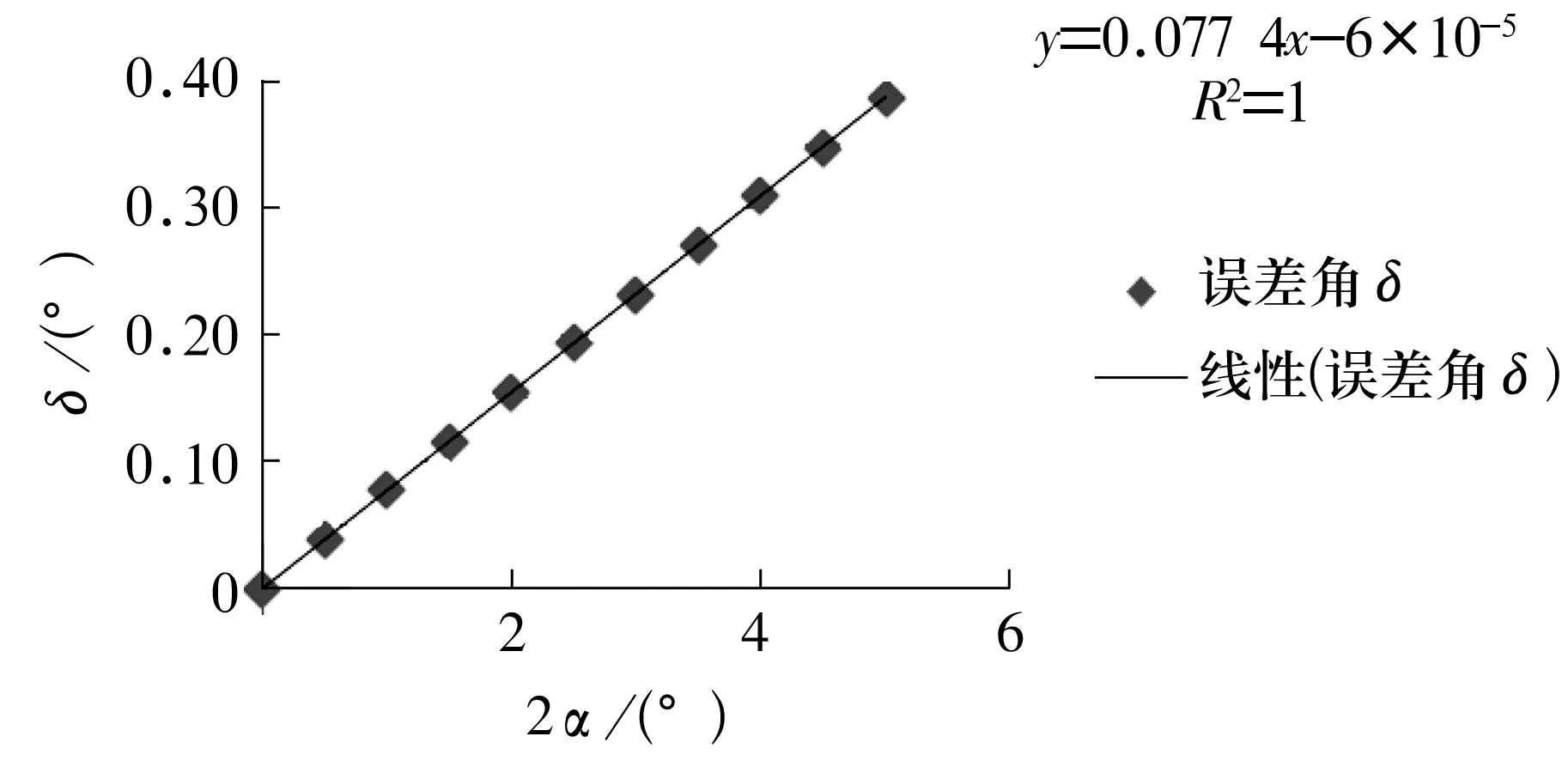
图3 120°V形定位块滚子角度误差与滚子角度回归分析

δ=0.077 4×2α-6×10-5。

(2)

从图3可以看出：该回归分析显著水平R2=1，说明误差角δ与圆锥角2α的线性程度非常高。但截距为-6×10-5≠0，且当2α=0时滚子为圆柱滚子，在V形定位块定位后误差角应为0，也与公式不符，说明δ与2α并不是完全的线性关系，只是在0°～5°内非常接近线性关系。因此，在0°～5°内可准确测得图2中滚子外素线与定位块基准的夹角2α′，采用(1)和(2)式反算出圆锥角2α(-6×10-5量级较小，计算中可省略)，即

2α=(2α′)/1.077 4。

(3)

3.3 采用V形定位的误差分析

根据以往经验，采用SOLIDWORKS2014建模分析得出的结果是可信的，但截距不等于0说明(3)式近似一阶线性回归。在0°～5°内通过SOLIDWORKS找点模拟可得(3)式计算数值与模拟实测值相差的数量级为10-5，另外的测量误差来源于V形定位块2个测量面与基准平面的角度、温度以及滚子外素线与定位块基准夹角2α′的测量误差。传统定位块测量的不确定度量级为10-4，其可以看做角度为180°的V形定位块。因此，结合(3)式的误差以及V形工作台的测量不确定度，在圆锥角0°～5°内采用V形定位台测量的不确定度量级应在10-4水平。

3.4 实例验证

选取3种圆锥角的滚子进行验证，其圆锥角分别为1°51′，2°15′，2°30′，均经过专业鉴定机构采用传统定位方法的鉴定，采用120°V形定位块定位和轮廓仪测量定位后的2α′，所得数据见表4。由表4中数据可知：实测值与传统定位块鉴定值偏差在10-4量级，即使考虑传统定位块鉴定的不确定度，两者误差仍未超过10-4量级，符合之前对误差的推断。

表4 120°V形定位块测2α′角度及偏差

4 结束语

通过上述分析可得：在0°～5°内使用V形定位块测量圆锥滚子圆锥角的方案正确可行，且操作方便，检测精度较高。而采用三维软件模拟分析，并对所得数据进行回归分析，使复杂的空间几何推导问题得以简化，对类似问题也提供了一种解决思路。

另外，误差角δ容易在测量过程中被忽视，在其他V形定位项目分析中也应予以重视；误差角δ与圆锥角2α应可以通过立体几何推导出准确的数学关系式，根据关系式可以进一步减小理论误差，且能扩大检测范围。