北斗/GNSS实时动态差分技术的实验教学解析

李克昭，石俊鹏，牛海鹏 ，马素霞

(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000；2. 北斗导航应用技术协同创新中心,河南 郑州 450052)

在光学测角、激光测距，甚至是全站仪测绘时代，都需要满足测站间的通视条件，前后站、测站至少需要4名测绘人员共同作业，存在作业效率低，劳动强度高的缺陷。GPS的出现，给测绘行业带来了翻天覆地的变化[1,2]。随着载波相位整周未知数快速求解技术和通信技术的快速发展，将基准站的观测数据及相关信息实时传输到移动台，移动台实时地进行载波相位差分处理，通常称为RTK(Real Time Kinematic)技术[3]。单个基准站覆盖的范围仅有20km左右[4]。网络技术的发展，为多基准站资源共享的RTK模式提供了技术支撑[5]。现行的网络RTK技术主要有虚拟参考站技术(VRS，Virtual Reference Station)[6]、区域改正数(FKP，德语：Flächen Korrektur Parameter，即Area Correction Parameter)技术[7,8]和主副站技术(MAC，Master-auxiliary Concept)[9-10]。北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)、Galileo系统的建设与全球运行，为实时动态差分技术的进一步发展与应用注入了活力。但不管是常规北斗/GNSS RTK,还是网络北斗/GNSS RTK技术，其基本工作原理都是载波相位动态差分原理，其关键技术都是获取基准站(或)CORS站与移动台之间的高精度基线向量。以下从导线测量的坐标增量与北斗/GNSS RTK基线向量的异同，以及二者坐标推算的特点和坐标转换问题入手，深入浅出地解析RTK关键技术。

1 北斗/GNSS RTK载波相位差分技术的基线向量与导线测量的坐标增量差异

传统的导线测量是通过测距、测角，并结合方位角的推算，得到两点间的坐标增量。图1给出了1条附合导线的测量示意图。

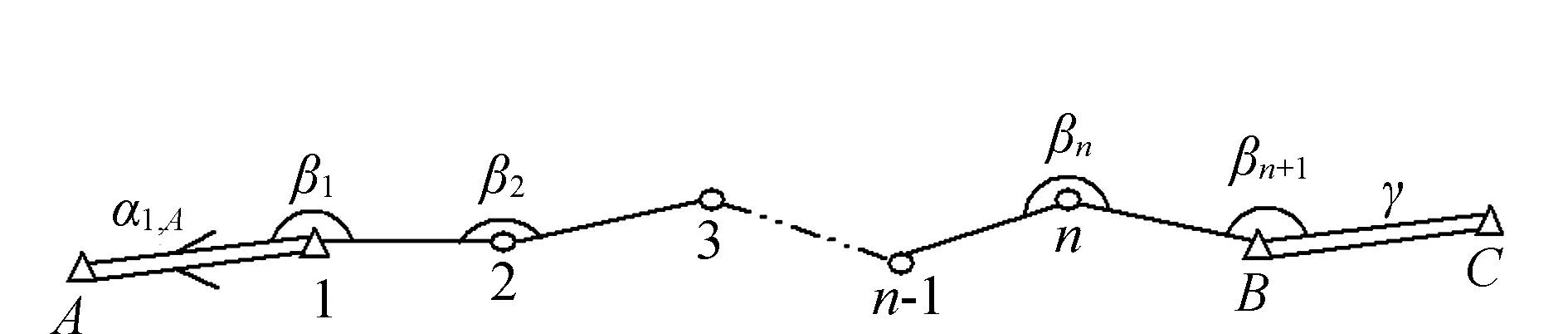
图1 附合导线测量示意图

如图1所示，可通过已知点A、1的坐标计算出起算方位角α1,A，

(1)

其它导线边的概略方位角可推算如下：

(2)

根据已知点B、C反算的方位角计算角度闭合差，如角度闭合差符合限差要求，修正观测角βi(i=1,2，…,n+1)，之后，进一步推算各导线边的方位角，并根据式(3)计算概略坐标增量。

(3)

式中：Si,i+1为导线边长。

计算B点的概略坐标，与其已知坐标求差得到坐标增量闭合差，判定精度是否满足导线测量精度要求。符合精度要求后，分配闭合差后，进一步修正坐标增量，最后，根据修正后的坐标增量推算各点的坐标。

而北斗/GNSS RTK测量技术是通过基准站与移动台的载波相位同步观测值之间求差，消除或削弱相关误差，构建新的虚拟观测方程，通过平差解算，得到两点之间基线向量。如图2所示，1号点设置基准站，2，3，…，n-1，n为移动台观测点。

图2 北斗/GNSS RTK测量示意图

根据北斗/GNSS理论，1号点的载波相位观测方程为

(4)

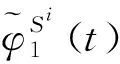
类似地，可写出t观测历元2，3，…，n-1，n号点的载波相位观测方程

(5)

(6)

(i=2,3,4,5,6)，

(7)

(8)

在相同历元和相同观测卫星条件下，上述载波相位观测方程分别与基准站1号点的载波相位观测方程进行测站之间求单差，得到虚拟观测方程。在基准站与移动站相距较近时，求差后电离层、对流层的延迟误差可以忽略不计。各个点相对基准站的虚拟观测方程可表示如下：

(i=1,2,3,4,5)，

(9)

(i=1,2,3,4,5)，

(10)

(i=2,3,4,5,6)，

(11)

(i=2,3,4,5,6).

(12)

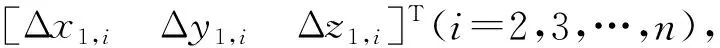
在导线测量中，当坐标增量确定后，导线点之间的相对位置关系也就确定了。类似地，在北斗/GNSS RTK测量中，当基线向量确定后，各测量点相对于基准站的位置，以及各测量点之间的相对位置也就确定了。不同之处在于导线测量的坐标增量是二维的、平面的，RTK的基线向量是三维的、立体的。

2 北斗/GNSS RTK基准站起算坐标的获取与坐标转换参数的配置

2.1 北斗/GNSS RTK基准站起算坐标的获取

对于导线测量而言，在获得坐标增量后，从起算点开始，后一个点的坐标等于前一个点的坐标加上该两点间的坐标增量，逐次递推而得。而对北斗/GNSS RTK而言，在获得移动台测站点相对于基准站的基线向量后，结合图2，移动台的测量坐标为

(13)

1)以基准站的已知坐标作为起算坐标。该坐标一般为北斗/GNSS静态控制测量的平差计算结果，也可以是导线测量、三角网测量或其他联合测量平差方式综合处理的坐标结果。

2)以基准站接收机的实时伪距定位结果作为起算坐标。在北斗/GNSS RTK的电子手薄软件中，设置基准站时，通常采用10次伪距平滑的方式获得基准站的起算坐标。

3)对于网络北斗/GNSS RTK，其基准站是CORS(Continuously Operating Reference Stations)站，当北斗/GNSS RTK电子手薄软件与CORS系统连接后，RTK系统在接收CORS站载波相位观测值的同时，还接收其概略坐标，作为北斗/GNSS RTK测量的起算坐标。

2.2 北斗/GNSS RTK坐标转换参数的配置

相对导线测量，北斗/GNSS RTK较难理解之处在于其坐标转换的问题。如GPS的测量成果是WGS-84坐标系的，而我国用户所需成果通常在北京54、西安80或者地方独立坐标系下，这就需要进行坐标成果转换。

通常北斗/GNSS RTK电子手薄的坐标参数计算与设置有2种方法：

1)根据测区的3个或3个以上公共已知点的两套坐标计算获得坐标转换参数。这种方法常与上述的以基准站已知坐标作为起算坐标法相配套。坐标参数的计算可通过式(4)计算：

(14)

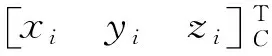
2)点校正法配置坐标参数。已知3个或3个以上控制点的用户坐标系坐标，在利用上述2.1中基准站起算坐标的获取2)、3)方法设置基准站坐标信息后，北斗/GNSS RTK移动台到3个或3个以上控制点上进行测量，获得其卫星测量坐标系下的坐标，然后调用北斗/GNSS RTK电子手簿的参数计算功能，获得该测量坐标系与用户坐标系之间的坐标转换参数。

说明：以GPS接收机为例，这里所提的卫星测量坐标系可以理解是在WGS-84椭球框架下的一种独立坐标系；上述2.1中2)、3)方法，每获得基准站的一个起算坐标，就等价于定义了一个WGS-84椭球框架下的独立坐标系。北斗/GNSS RTK测量时，首先是在该卫星坐标系下获得一个测量结果，然后，再根据所设置的坐标参数给出坐标转换后的结果，即用户坐标系下的成果。

3 实例与数据分析

为了进一步加深对北斗/GNSS RTK技术的理解，设计实验：以莱卡TS02全站仪(测角2 s，测距2 mm+2 ppm)按照三级导线测量技术要求，进行附合导线测量(如图3所示)，以测量结果作为验证RTK测量的基准，导线待定点测量处理结果见表1所示。

图3 附合导线实验示意图

针对以上导线待定点，利用中海达V30 GNSS接收机，进行3种RTK测量方法验证：

方法1：已知点设置基准站，起算坐标采用已知点坐标，坐标转换参数采用已知点测量坐标系与用户坐标系对应的转换参数；

方法2：任意点设置基准站，起算坐标采用基准站的伪距10次平滑结果，坐标转换参数采用点校正法获得；

方法3：网络RTK法，起算坐标采用CORS站发送的基准站概略坐标，坐标转换参数采用点校正法获得。

测量结果分别见表2—表4。

表1 导线待定点测量处理结果 m

表2 RTK方法1测量结果 m

表3 RTK方法2测量结果 m

表4 RTK方法3测量结果 m

3种RTK方法测量结果与导线测量的点位较差结果见图4所示。

图4 3种RTK测量方法与导线测量的较差

从图4可见，3种RTK测量方法与三级导线的测量结果较差都在cm级，因此，说明3种RTK测量的基准站设置、转换参数配置都是正确的。

4 结束语

论文从测绘工作者熟悉的导线测量入手，比较了导线测量的坐标增量与北斗/GNSS RTK测量的基线向量的异同，分析了导线与北斗/GNSS RTK测量坐标推算的异同，阐释了北斗/GNSS RTK坐标推算的起算坐标选取与坐标转换参数配置问题；最后，以三级导线测量为比较基准，进行了3种GPS RTK测量方法的验证。验证结果表明，以已知点或任意点设置基准站的常规北斗/GNSS RTK方法，或网络北斗/GNSS RTK方法，都可以获得cm级的测设结果。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J],测绘学报, 2010 (1):1-6.

[2] 张睿,杨元喜,张勤，等.BDS/GPS联合定轨的贡献分析[J], 武汉大学学报(信息科学版), 2017(5): 600-608.

[3] 李克昭, 杨力, 柴霖，等. GNSS定位原理[M].北京：煤炭工业出版社, 2014: 185-195.

[4] Mustafa Berber, Niyazi Arslan. Network RTK: A case study in Florida [J]. Measurement, 2013, 46(2013): 2798-2806.

[5] 梁霄, 杨玲, 黄涛，等. 网络RTK基准站间的模糊度及空间相关误差解算[J]. 测绘工程, 2016, 25(1): 24-28.

[6] 黄丁发, 周乐韬, 刘经南，等. 基于Internet的VRS/RTK定位算法模型及实验研究[J]. 武汉大学学报(信息科学版), 2007, 32(3): 220-225.

[7] 祝会忠, 徐爱功, 高星伟，等. 长距离GNSS网络RTK算法研究[J]. 测绘科学, 2014, 39(5): 80-83.

[8] ZHANG Liang, LV Hanfeng, WANG Dingjie etc. Asynchronous RTK precise DGNSS positioning method for deriving a low-latency high-rate output [J]. J Geod, 89:641-653.

[9] 姚宜斌, 胡明贤, 许超钤. 基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009-1017.

[10] FENG Yanming, GU Shengfeng, SHI Chuang, et al. A reference station-based GNSS computing mode to support unified precise point positioning and real-time kinematic services [J]. J Geod, 2013, 87:945-960.