北斗三频数据的周跳探测与修复方法研究

许亚辉,姚宜斌

(武汉大学 测绘学院，湖北 武汉 430079)

我国北斗卫星导航定位系统目前能够播发B1,B2,B3 3个频段的信号，是国际导航系统的重要组成部分[1]。北斗三频载波信号的周跳探测与修复是实现系统高精度定位的前提保证。目前常用的周跳探测方法有伪距相位组合法、无几何相位法、电离层残差法、多普勒积分法等方法[2]。本文联合伪距相位组合法以及无几何相位法进行北斗三频数据周跳的探测与修复，构成了2个伪距相位组合以及1个无几何相位组合共3个线性无关的周跳检测量。通过对实测的北斗三频数据进行周跳探测，可以探测出包括1周在内的所有周跳组合，且无敏感周跳组合。

1 北斗三频观测值周跳的探测与修复

1.1 北斗三频组合观测值

当采样间隔较小时，由于在相邻历元间求单差可以消除或减弱卫星钟差、接收机钟差、多路径效应等误差的影响，因此这些误差在本文中不予考虑[3]。

北斗单频非差载波相位观测方程为

(1)

式中：i=1,2,3分别为北斗信号的B1,B2,B3 3个频率；λi,φi,Ni,εφi分别为相应频率的载波波长，载波相位， 整周模糊度和观测噪声；R为测站和卫星之间的几何距离；τtrop为对流层延迟误差；δr为卫星轨道误差；Iion,1为北斗B1载波相位的电离层延迟。

根据三频组合理论[4-6]，北斗三频载波相位组合观测值为

(R+τtrop+δr)-(iN1+jN2+kN3)-

(2)

将(2)式整理得：

λ(i,j,k)φ(i,j,k)=R+τtrop+δr+λ(i,j,k)N(i,j,k)-

Q(i,j,k)Iion,1+λ(i,j,k)ε(i,j,k)，

(3)

其中，λ(i,j,k),N(i,j,k),Q(i,j,k)分别为组合观测值的波长、整周模糊度以及电离层延迟系数。(i,j,k)均为整数，且不全为零，由此可保证组合观测值整周模糊度的整数特性。

北斗单频非差伪距观测方程为

(4)

式中，Pi为单频伪距观测值；εPi为单频伪距观测噪声。

北斗三频伪距组合观测值为

P(α,β,γ)=α·P1+β·P2+γ·P3=

R+τtrop+δr+Q(α,β,γ)·Iion,1+ε(α,β,γ).

(5)

式(5)中伪距组合系数之和为1，即α+β+γ=1，因此可以保证组合后的观测值卫地距离、对流层延迟、卫星轨道误差保持不变。Q(α,β,γ),ε(α,β,γ)分别

为三频伪距组合观测值的电离层延迟系数和观测噪声。

1.2 北斗三频伪距相位组合法探测周跳

1.2.1 伪距相位组合法

由式(3)减去式(5)可得：

K·Iion,1+ε(i,j,k,α,β,γ)，

(6)

将式(6)在相邻历元间求差，即：

ΔN(i,j,k)=N(i,j,k)(t1)-N(i,j,k)(t2)=

(7)

其中，Δ表示在历元t1,t2间求差。ΔN(i,j,k)即为北斗三频伪距相位组合观测值的周跳检测量。由式(7)可知，组合观测值的周跳探测精度取决于组合噪声、组合波长以及电离层延迟在相邻历元间的变化[7]。在采样率为1 Hz/s或更高采样率的条件下，历元间电离层延迟变化非常小，因此在较高采样率情况下，可忽略历元间电离层延迟量[8]。假设北斗3个频率的载波相位观测值以及伪距观测值都是相互独立的，则有载波相位观测噪声σφ1=σφ2=σφ3=σφ=0.01周，伪距观测值噪声σP1=σP2=σP3=σP=0.5m[8]，根据误差传播定律可得

(8)

1.2.2 伪距相位组合法组合系数的选取

当周跳检测量大于其n倍中误差时，认为发生了周跳，即：

ΔN(i,j,k)>nσΔN(i,j,k).

(9)

n=3或4时，其置信水平分别为99.7%和 99.9%。为了使组合观测值具有组合波长较长、组合电离层延迟系数较小、组合噪声较小的特性，应选取优良的组合系数以满足上述特点。

根据表1所示，组合系数(-1,-5,6)所构成的伪距相位组合观测值有着较长的波长，但电离层延迟误差系数较大。组合系数(1,1,-2)所构成的组合观测值虽然有着较小的电离层延迟误差系数，但组合波长较小，观测噪声较大。因此，通过比较几组组合观测值的特性，本文选取(0,-1,1),(1,4,-5)作为伪距相位组合法的两组系数。

表1 伪距相位组合法不同系数的组合观测值及其属性

1.3 北斗三频无几何相位法探测周跳

无几何相位法指组合后的载波相位观测值的卫地距离为零，即组合系数之和a+b+c=0，其方程为

B(a,b,c)=aλ1φ1+bλ2φ2+cλ3φ3=

-(aλ1N1+bλ2N2+cλ3N3)-

(10)

其中，B(a,b,c)为无几何相位组合观测值，N(a,b,c)为组合观测值整周模糊度，Q(a,b,c)为电离层延迟系数，ε(a,b,c)为组合观测值噪声。

将式(10)在历元间求差可得:

ΔN(a,b,c)=-ΔB(a,b,c)-Q(a,b,c)·

ΔIion,1/λ1+Δε(a,b,c)=

-(aλ1Δφ1+bλ2Δφ2+cλ3Δφ3)-Q(a,b,c)·

ΔIion,1/λ1+Δε(a,b,c).

(11)

当电离层延迟系数较小时，可忽略其影响，根据误差传播定律，无几何相位法周跳检测量的中误差为

(12)

无几何相位法周跳检测量主要受组合观测值的电离层延迟误差以及观测噪声的影响，在选取组合系数时，应满足电离层延迟误差较小、观测噪声较小的特性。根据以上要求，本文在[-5,5] 整数范围内，选取较优的无几何相位组合系数。

根据表2所示，组合系数(1,3,-4)所构成的无几何相位法组合观测值有着最小的电离层延迟误差系数，但观测噪声较大。通过比较几组组合观测值的特性，本文选取(1,1,-2)作为无几何相位法的组合系数。

表2 无几何相位法不同系数的组合观测值及其属性

1.4 不敏感周跳的探测

无论是伪距相位组合法还是无几何相位法，当三频载波存在的周跳恰好能使组合后观测值的周跳检测量接近于零时，两种周跳探测方法失效，三频载波上存在的周跳即为不敏感周跳组合。对于伪距相位组合法，前文已确定其最优组合系数为(0,-1,1),(1,4,-5)，现在假设两个组合系数下三频载波相位观测值的不敏感周跳组合为ΔN1,ΔN2,ΔN3，忽略电离层延迟和观测噪声的影响，该方法的周跳检测量为

ΔN(i,j,k)=i·ΔN1+j·ΔN2+k·ΔN3,

(13)

将两组系数代入上式，可得

(14)

解方程组可知，ΔN1=ΔN2=ΔN3为不敏感周跳组合，即三个载波的周跳值相同时，利用伪距相位组合法无法探测出周跳的存在，为了避免这种情况，现联合无几何相位法共同探测周跳。

对于无几何相位法，组合观测值的周跳检测量为

ΔN(a,b,c)=a·λ1·ΔN1+b·λ2·

ΔN2+c·λ3·ΔN3.

(15)

当ΔN1=ΔN2=ΔN3时，伪距相位组合法失效，若此时无几何相位法的周跳检测量也小于3倍中误差，即ΔN(a,b,c)<3·σΔN(a,b,c)=0.024，则两种方法均失效。将ΔN1=ΔN2=ΔN3带入式(15)及不等式，解得

-0.743<ΔN1=ΔN2=ΔN3<0.743.

(16)

即当两种方法均失效时，北斗三个频段的周跳值应该都相等且绝对值小于0.743，但这种情况不存在。因此联合伪距相位法和无几何相位法可以探测到包括1周在内的所有周跳组合。

1.5 周跳的确定与修复

联合伪距相位组合法以及无几何相位法，可以构造出3个线性无关的周跳检测量。令组合系数矩阵为A，原始载波周跳矩阵为X，周跳检测量矩阵为L，三者满足如下关系：

AX=L.

(17)

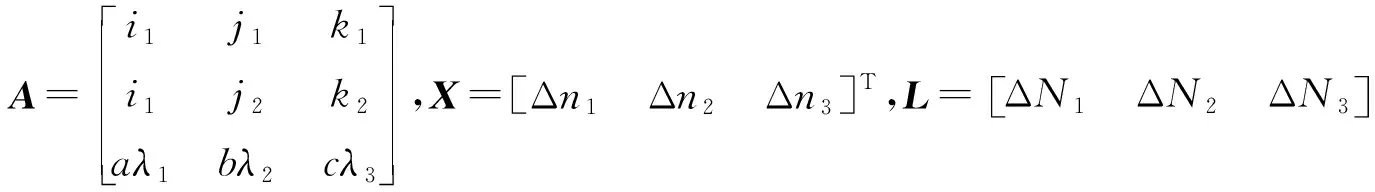
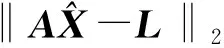
2 实验验证与分析

本文采用北斗实测数据进行实验，实验分析使用的卫星是北斗C12号卫星，数据采集时间为2017-04-17T23:00—24:00，采集地点为珠海，数据采样间隔为5 s，共720个历元。利用本文提出的周跳探测方法，首先对原始数据进行周跳探测，图1是利用伪距相位组合法对原始数据进行的探测，探测结果显示原始数据无周跳。

2.1 高采样率数据中的小周跳组合探测

本小结使用的实验数据是采样间隔为5 s的高采样率原始数据，为探测出在高采样率数据中的小周跳，实验中人为在原始数据的第100、200、400历元处分别添加(1,0,0)、(0,2,1)、(0,2,1)3个周跳组合，这3种情况下周跳检测量的理论值如表3所示。利用前文所述方法，对本节人为添加的小周跳组合进行探测，结果如图2(a)—图2(c)所示。

图1 原始数据无周跳

表3 高采样率数据加入小周跳组合的位置和相应周跳检测量理论值

图2 高采样率小周跳组合探测

图2(a)—图2(c)分别是在高采样率的原始数据上添加不同小周跳组合后的周跳检测量变化图。从表3可以得知，当只有B1波段发生周跳时，即人为添加(1,0,0)周跳组合后，伪距相位组合法组合系数(0,-1,1)构成的周跳检测量小于3倍中误差，理论上无法探测出该周跳。但组合系数(1,4,-5)及无几何相位法组合系数(1,1,-2)构成的周跳检测量，理论上可以分别探测出该周跳，且理论值分别为1和0.192，均大于3倍中误差，图2(a)验证了该结论。图2(b)中，3个组合均可单独探测出高采样率数据中的小周跳组合。当3个波段的周跳值相同，伪距相位组合法出现不敏感周跳时，该方法失效，实验中在3个波段加入(1,1,1)周跳组合，虽然伪距相位组合法无法探测出，但理论上可以利用无几何相位法探测出该周跳组合，周跳检测量为-0.032，图2(c)验证了该结论。

2.2 高采样率数据中的大周跳组合探测

使用的实验数据是采样间隔为5 s的高采样率原始数据，为探测出在高采样率数据中的大周跳，试验中人为在原始数据的第100、200、400历元处分别添加(30,10,40)、(130,25,53)、(9,7,18)3个周跳组合，这3种情况下周跳检测量的理论值如表4所示。利用前文所述方法，对本节人为添加的大周跳组合进行探测，结果如图3(a)—图3(c)所示。

图3(a)—图3(c)分别是在高采样率的原始数据上添加不同大周跳组合后的周跳检测量变化图。

表4 高采样率数据加入大周跳组合的位置和相应周跳检测量理论值

图3 高采样率大周跳组合探测

当在100历元处人为添加(30,10,40)周跳组合时，两种方法联合探测周跳的理论检验量分别为30、-130、-10.669，图3(a)验证了该结论。以此类推，图3(b)、图3 (c)也分别验证了理论值。因此，图3所示的周跳检测量探测值与表2中周跳检测量理论值均一致，即在高采样率的情况下，无论原始数据哪一个波段发生周跳，周跳无论大小，利用伪距相位组合法以及无几何相位法，均可以探测出这些周跳。

2.3 低采样率数据中的随机周跳组合探测

将原始数据提取成采样间隔为15 s，共240个历元的低采样率数据，在此基础上人为添加随机周跳组合，所添加周跳组合的位置、大小和周跳检测量理论值如表5所示。通过本节实验，来检验两种方法对于低采样率数据，不同大小的周跳组合的探测与修复效果，实验结果如图4所示。

图4(a)—图4(f)分别是在低采样率数据上添加随机周跳组合后的周跳检测量变化图。同前面的分析，图4所示的周跳检测量探测值与表3中周跳检测量理论值均一致。当在低采样率的情况下出现伪距相位组合法不敏感周跳时，即图4(f)所示的在3个波段分别发生1周的跳变，利用无几何相位法依然可以探测出该周跳，周跳检测量大于无几何相位法观测噪声3倍中误差。因此，对于低采样率数据，不同大小的随机周跳组合，利用伪距相位组合法和无几何相位法联合探测，均能将各类周跳探测出，也不存在不敏感周跳组合。

表5 低采样率数据加入随机周跳组合的位置和相应周跳检测量理论值

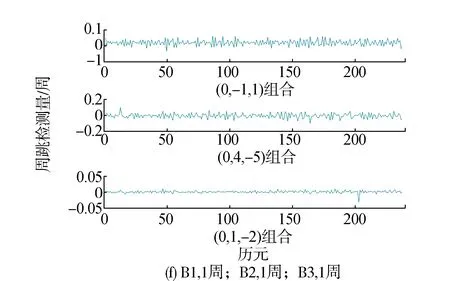
图4 低采样率随机周跳组合探测

3 结 论

本文联合伪距相位组合法以及无几何相位法进行北斗三频数据周跳的探测与修复，通过筛选优良的组合系数，构成了2个伪距相位组合(0,-1,1),(1,4,-5)以及1个无几何相位组合(1,1,-2)共3个线性无关的周跳检测量。本文实验选取了实测的北斗三频数据，并分别对高采样率数据的小周跳组合、高采样率数据的大周跳组合以及低采样率数据的随机周跳组合进行探测。实验结果显示，无论是高采样率数据还是低采样率数据，两种方法结合可以探测出包括1周在内的所有周跳组合，且无敏感周跳。本文以2范数最小为准则进行周跳修复，保证了周跳探测的准确性。

[1] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报,2010(1):1-6.

[2] XU G. GPS: Theory, Algorithms and Applications, 2nd edition by Guochang Xu[J]. Berlin: Springer,2007.

[3] 姚一飞,高井祥,王坚,等. 北斗三频载波观测值的周跳实时探测与修复[J]. 中国矿业大学学报,2014(6):1140-1148.

[4] ZHANG W. Triple Frequency Cascading Ambiguity Resolution for Modernized GPS and GALILEO[J]. 2005.

[5] RICHERT T, EL-SHEIMY N. Optimal linear combinations of triple frequency carrier phase data from future global navigation satellite systems[J]. GPS Solutions, 2007, 11(1):11-19.

[6] URQUHART L. An Analysis of Multi-Frequency Carrier Phase Linear Combinations for GNSS[C]// 37th COSPAR Scientific Assembly. 37th COSPAR Scientific Assembly, 2008:3261.

[7] 孙保琪,欧吉坤,盛传贞,等. 一种适于Compass周跳探测的三频数据优化组合[J]. 武汉大学学报(信息科学版),2010(10):1157-1160.

[8] 罗腾,白征东,过静珺. 两种周跳探测方法在北斗三频中的应用比较研究[J]. 测绘通报,2011(4):1-3，13.

[9] WANG K, ROTHACHER M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data[J]. Journal of Geodesy, 2013, 87(6):539-553.

[10] LIU Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver[J]. Journal of Geodesy, 2011, 85(3):171-183.

[11] 李迪,柴洪洲,潘宗鹏,等.基于伪距相位和STPIR组合的北斗三频周跳探测与修复[J].测绘工程,2017,26(5):71-75,80.

[12] 肖国锐,隋立芬,戚国宾,等. 一种改正伪距多路径误差的北斗三频周跳探测与修复方法[J]. 大地测量与地球动力学,2015(4):671-675.

[13] 宁一鹏,王坚,扈旋旋,等. 惯性辅助强多径环境中的北斗三频周跳探测与修复[J].测绘学报,2016(增2):179-187.

[14] 谢建涛,隋春玲,郝金明,等. 利用北斗三频非差数据进行周跳实时探测与修复[J]. 武汉大学学报(信息科学版),2016(12):1638-1642.

[15] 黄令勇,宋力杰,王琰,等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报,2012(5):763-768.