基于COMSOL连铸坯壳测厚横波EMAT优化

王志春，袁伟



基于COMSOL连铸坯壳测厚横波EMAT优化

王志春，袁伟

(内蒙古科技大学信息工程学院，内蒙古包头 014010)

为了研究电磁超声传感器(Electromagnetic Acoustic Transducer，EMAT)横波测量连铸坯壳厚度的机理及横波在连铸坯中的传播情况，选取坯壳厚度为10～50 mm的Q235小方坯为研究对象，利用有限元软件COMSOL建立脉冲电磁铁和螺旋线圈的电磁超声模型，分析在不同EMAT结构参数下，连铸坯中电磁场、力场、声场的分布规律。研究结果表明：脉冲电磁铁和螺旋线圈组成的EMAT能够在连铸坯壳集肤层激发出超声波横波。脉冲电磁铁空心螺线管线圈匝数、内半径、线圈导线半径对换能效率的影响依次减小，且当脉冲电磁铁内半径尺寸大于螺旋线圈尺寸时，产生横波的效率最高。坯壳厚度越小，螺旋线圈最优激励频率越大，测量精度越高，信号衰减越快。因此，坯壳厚度为10～50 mm的Q235小方坯选择1.1 MHz为最佳激励频率。

连铸坯壳；电磁超声换能器；横波；测厚；有限元建模

0 引言

对坯壳厚度进行实时监测在连铸生产过程中有着重大的意义。传统的射钉法和电涡流法无法满足无损检测和测量范围的需求。电磁超声法是通过电磁耦合的方法在试件内激发超声波，既克服了超声法需要耦合剂的缺点[1]，又满足了大范围坯壳厚度的测量要求。本文主要研究连铸小方坯Q235坯壳厚度的电磁超声横波法在线检测。由于被测体温度高达800℃以上，目前国内电磁超声横波在高温环境中进行厚度测量的研究尚未有报道[2]。

超声波横波和纵波都可用于厚度的测量，横波的速度为纵波的一半左右，在同一频率下横波的测量精度是纵波的两倍[3]。在小方坯Q235连铸生产过程中，根据拉速、过热度的不同，坯壳厚度在10～50 mm之间[4]。本文根据目前的研究成果，提出采用收发一体脉冲式电磁超声传感器(Electromagnetic Acoustic Transducer，EMAT)激发超声波横波，用有限元仿真软件COMSOL对超声波横波测连铸凝固坯壳厚度EMAT进行优化，进而指导连铸坯壳电磁超声横波测厚仪的研制。

1 EMAT的换能机制以及其数学模型

EMAT主要由三部分构成：脉冲电磁铁、螺旋线圈、连铸坯被测试件。图1为其结构示意图。

图1 三维 EMAT结构示意图

当永磁铁处于高温下，会失去磁性或工作点偏移较大，导致无法工作，因此，本文使用无铁芯的空心螺线管作为脉冲电磁铁来代替永磁体产生静态磁场。根据电磁学相关理论[5]，通过式(1)可计算出空芯螺线管底面中心位置沿轴线的磁感应强度：

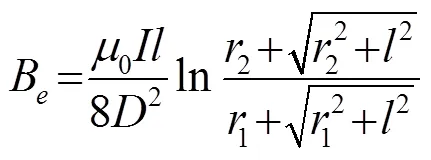
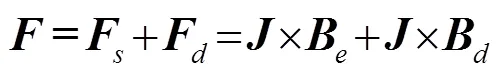
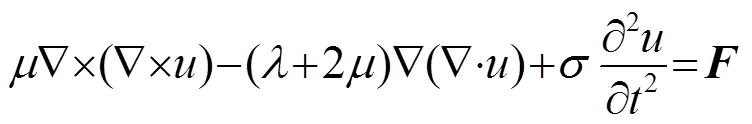
2 EMAT有限元建模

2.1 被测对象分析

本文主要研究电磁超声法测量结晶器下连铸Q235钢的坯壳厚度，根据其材料特性以及相关研究[6]，将其分为固态区、液态区、固液两相区。由于超声波横波只在固态中传播，所以本文将被测试件分为两层，固态区一层，液态区和两相区一层，分别探讨超声波在其中的传播情况。在连铸过程中，即使是铁磁性钢种，在高于其居里点的温度下，磁矩重新排列，对外显示顺磁性，故文中只考虑洛伦兹力机制下的EMAT[2]。

2.2 参数化建模

利用COMSOL有限元仿真软件对横波测量连铸坯壳厚度进行二维多物理场仿真分析，其中包括EMAT横波的发射和接收。其结构图如图2所示，主要包括：空气域、螺旋线圈、脉冲电磁铁、被测试件。

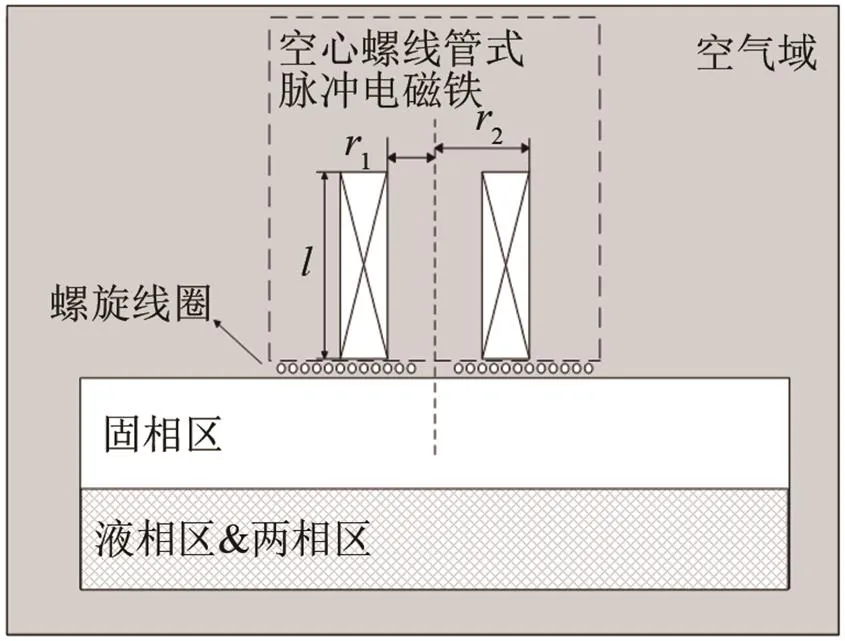
图2 二维实体建模示意图

该模型使磁场、固体力学、压力声学物理场相互耦合，并使用手动网格剖分、瞬态求解类型、广义计算方法进行运算。最后进行参数化扫描、参数优化等步骤进行后处理。设置EMAT参数如表1所示。

表1 实体建模待优化参数设置

其余参数均为定量。被测试件连铸坯壳模型宽为200 mm，每层高为30 mm。在高温下，引起超声波横波速度减小的主要原因是杨氏模量的改变，密度和泊松比看做常量[7]。密度为7 860 kg.m-3，泊松比为0.28，杨氏模量为4 494.1 MPa(800～1 300℃多点求平均值[8])。线圈模型匝数为15，提离为0.5 mm，线间距为0.1 mm，激励线圈函数为tone-test信号，信号周期数为8，峰值为100 A。

2.3 模型验证及分析

选择合适的网格划分和计算步长，通过计算可得出坯壳为30 mm时不同时刻横波在连铸坯中的传播情况。

由图3可知，超声波在坯壳表面产生，并向下传播，超声波传播、衰减趋势与理论一致，验证了模型的正确性。但当超声波到达底面后，能量变得不集中，向四周发散，且在两相区和液相区有较强的纵波穿透，说明洛伦兹力分量远远大于分量。

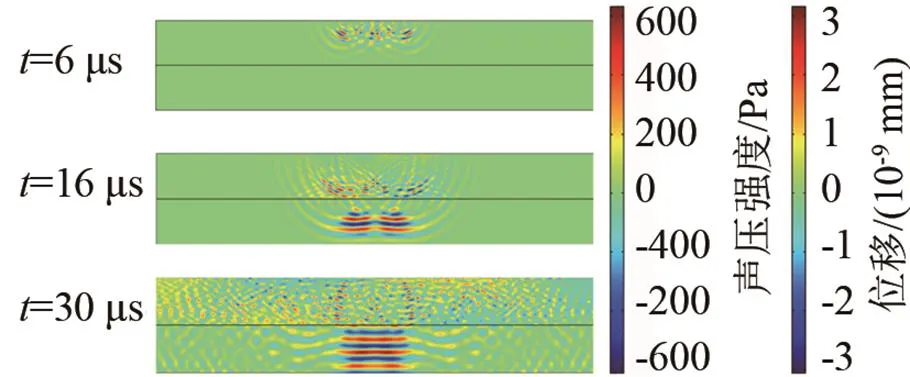
图3 优化前超声波在试件内传播情况

此现象与脉冲电磁铁、螺旋线圈的参数密切相关，因此对EMAT的结构参数进行优化是非常必要的。

3 EMAT的优化设计

根据EMAT的结构特点，本文对脉冲电磁铁和螺旋线圈分别进行优化。

3.1 脉冲电磁铁的优化

3.1.1 线圈结构尺寸的优化

表2 线圈结构参数正交实验结果数据表

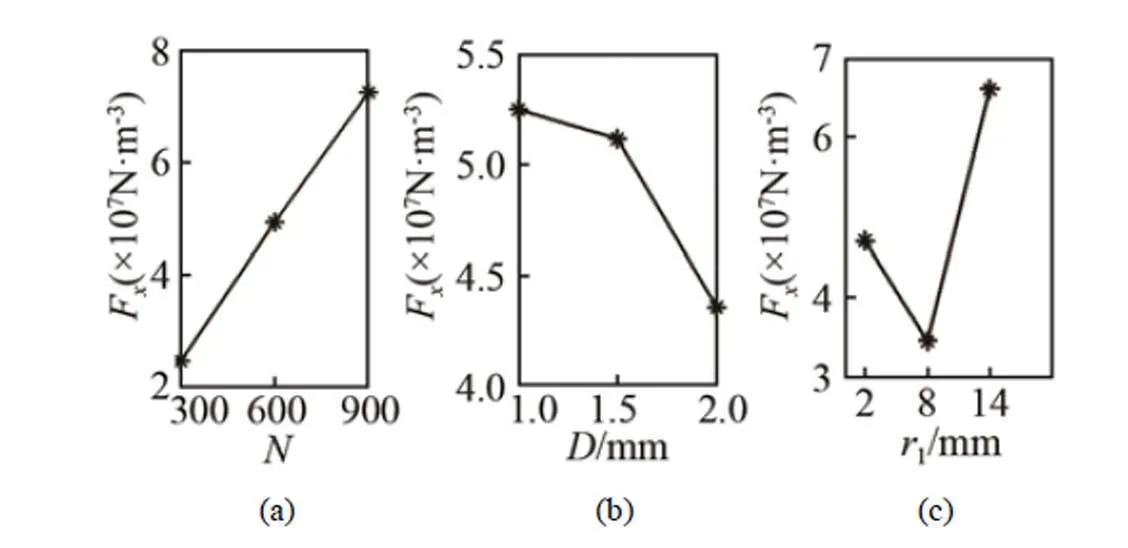
图4 Fx 随参数N、D、r1的变化趋势图

3.1.2 线圈激励的优化

相比于其他类型的电磁铁，脉冲电磁铁最大的优点就是在开始工作的瞬间可以建立起需要的磁场，持续相应时间后迅速消失。本文中线圈的激励信号是一个方波。确定线圈匝数、线圈导线半径等参数后，通过控制电流的大小控制磁场强度。

由图5可知，磁通密度模和洛伦兹力均随着线圈激励的增大而增大，且洛伦兹力的增大速度更快。考虑到成本和安全问题，本文选择两条线的交汇处，即脉冲电磁铁激励电流选择190 A即可。

图5 磁通密度模和洛伦茲力随脉冲电磁线圈激励电流的变化

3.2 螺旋线圈优化

感应电流密度和激励频率分别是决定信号强度和信号衰减的重要因素。通过正交分析法得出提离距离、线圈线半径、线间距对感应电流密度的影响程度依次减小[10]。提离距离越小，收到的回波的信号越大，所以在保证安全和相应工艺要求的情况下，尽量减少提离距离，而线间距又与线圈激励频率有关，因此，只需要对线圈导线半径和激励频率进行优化。

3.2.1 螺旋线圈线半径的优化

根据被测试件的要求，使用钨丝来绕制螺旋线圈以防止高温对线圈的影响。选择线圈正下方被测试件集肤表层内任意一点的坐标(4 mm，-0.1 mm)，观察该点感应电流的密度随线圈导线半径的变化趋势。

从图6中可以看出，随着的增大，感应电流密度先增大后减小。当为0.3 mm时，感应电流密度达到最大值，该值处有利于增强换能效率，增强回波幅值。因此，本文选择为0.3 mm的线圈为螺旋线圈。

3.2.2 螺旋线圈激励频率的优化

超声波的波长决定着超声波的衰减程度。频率越大，衰减越快，但精度越高。所以根据被测试件的物性特点，选择最佳激励频率。连铸小方坯的坯壳厚度在10～50 mm左右。如果要增强回波信号，必须增强激励信号，减少衰减。图7为当连铸坯壳厚度为30 mm时，线圈正下方被测试件集肤表层内任意一点坐标(10 mm，-0.1 mm)处不同频率下的感应电流密度和洛伦兹力的大小。

图6 感应电流密度随线圈线半径的变化

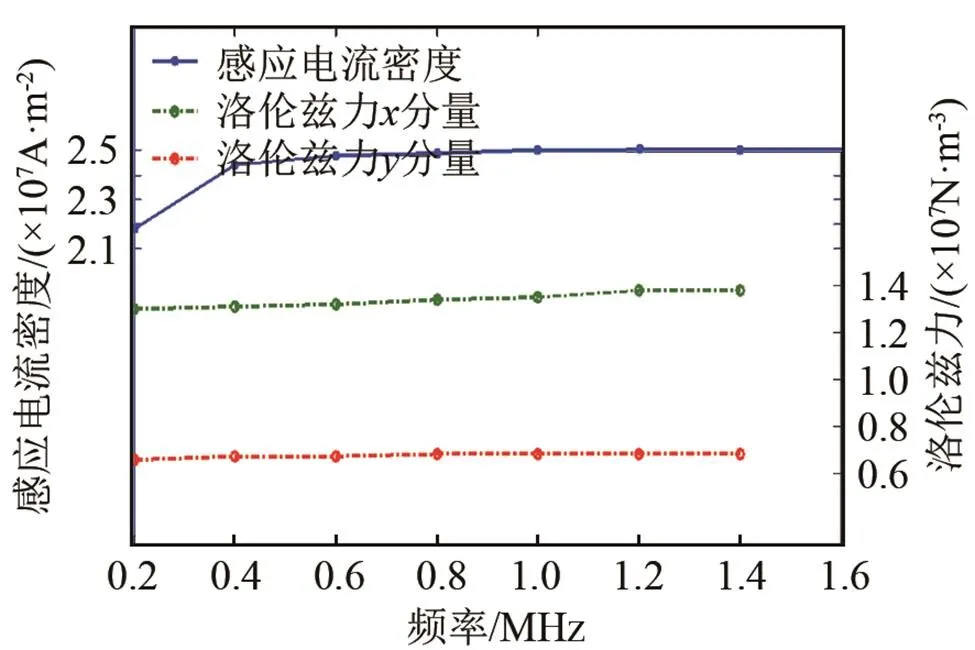
图7 感应电流密度随激励频率的变化

由图7可知，线圈激励频率对感应电流和洛伦兹力的大小几乎没有影响，因此只考虑衰减情况。并且可以看出洛伦兹力分量远远大于洛伦兹力分量，更加证实了模型的正确性，确定所激发的波型为横波。

超声波频率越小，衰减越小，接收信号越大，但是同时回波信号的干扰也越大。所以要想选出最佳激励频率，不能仅依靠回波信号的幅值大小，必须依靠信号的实时传播情况。图8和图9为线圈正下方被测试件集肤表层内任意一点坐标(8 mm，-0.1 mm)的实时振动情况。激发时质点的振动幅度是由脉冲电磁铁和线圈激励共同决定的，待超声波向下传播时，超声波产生叠加，导致了回波强度大于激发超声波强度的假象。超声波激发过程中产生横波和一小部分纵波。由横波和纵波的传播速度可知，位移信号较小的为纵波回波，位移信号较大的为横波回波。

由图8可得，当坯壳厚度为50 mm时，从接收信号的位移分布来看，最佳激励频率为0.9 MHz；当厚度为30 mm时，最佳激励频率为1.1 MHz。而当坯壳厚度为10 mm时，由于厚度较薄，激励频率为0.7～1.5 MHz时，波形出现叠加或杂乱现象，直至2.1 MHz，方可清晰地观察到信号回波，如图9 所示，但信号衰较快。由此可以看出，在其他条件相等的情况下，频率和厚度具有一定的关系，厚度越小，最佳激励频率越大，衰减越快。综合考虑，选择中间频率1.1 MHz。

图8 0.7～1.5 MHz频率下质点位移情况

图9 2.1 MHz频率下质点位移情况

通过仿真优化，最终确定优化后的参数并保持其他参数不变，得出不同时刻连铸坯中超声波的传播情况。由图10可知，超声波在坯壳表面产生，并垂直向下传播，横波到达固液分界面后立即返回，纵波继续向两相区传播。但优化后纵波的声强方向明显减小。

图10 优化后超声波在试件内传播情况

4 结论

脉冲电磁铁和螺旋线圈相组合产生的EMAT，有效地在连铸坯壳内激发出超声波横波，并伴随着微小的纵波。

脉冲电磁铁空心螺线管线圈匝数、内半径1、线圈导线半径对换能效率的影响依次减小。当内半径1大于螺旋线圈半径时，产生横波的效率最高。磁场强度、洛伦兹力与匝数成正比，与线圈导线半径成反比。脉冲电磁铁空心螺线管最优参数：为900，1为14 mm，为1 mm。

(3) 螺旋线圈激励频率的大小，几乎不影响坯壳表面感应电流和洛仑兹力的大小，但改变信号的衰减情况。当坯壳厚度越小时，最佳激励频率越高，精度越大，衰减越快。经过综合考虑，坯壳厚度为10～50 mm的Q235小方坯选择1.1 MHz为最佳的激励频率。

本文旨在优化传感器，使传感器用于连铸小方坯测厚，以提高灵敏度，减少误差。高温对超声波的传播有一定的影响，后续将经过试验，对温漂等影响进行修正。横波EMAT在连铸小方坯测厚方面有重要意义，在以后的工作中会对其进行不断的探究与改善。

[1] 闻小德, 刘超群. 电磁超声探伤仪在棒材检测中的应用[J]. 声学技术, 2015, 34(5): 419-423.WEN Xiaode, LIU Chaoqun. Application of electromag-netic ultrasonic flaw detector in bar testing[J]. Technichal Acoustics, 2015, 34(5): 419-423.

[2] 欧阳奇, 陈希梦, 张兰兴, 等. 连铸坯集肤表层电磁激励超声场模拟[J]. 钢铁研究学报, 2016, 28(6): 78-82. OUYANG Qi, CHEN Ximeng, ZHANG Lanxing. Ultrasonic field simulation of electromagnetic stimulation on skin surface of continuous casting billet[J]. Journal of Iron and Steel Research 2016, 28(6): 78-82.

[3] 曹建海, 严拱标, 韩晓枫. 电磁超声测厚原理及应用-一种新型超声测厚法[J]. 浙江大学学报(工学版), 2002, 36(1): 88-91.CAO Jianhai, YAN Gongbiao, HAN Xiaofeng. The principle and appli-cation of electromagnetic ultrasonic thickness measurement -a new method of ultrasonic thickness measurement[J]. Journal of Zhejiang University(Engineering Edition), 2002, 36(1): 88-91.

[4] 曹远峰,张永鑫,刘新. 小方坯连铸机高速结晶器的研究[J]. 重型机械,2001,6(4):13-18.CAO Yuanfeng, ZHANG Yongxin, LIU Xin. Study on high speed crystallizer of small billet caster[J]. Heavy Machinery, 2001,6(4):13-18.

[5] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000: 186-189. FENG Cizhang, MA Xikui. Introduction to engineering electromagnetic field[M]. Beijing: Higher Education Press, 2000: 186-189.

[6] 王志春,张楼成,袁小健. 基于ANSYS的45#钢结晶器内温度场模拟[J]. 铸造,2016,65(9):879-882.WANG Zhichun, ZHANG Loucheng, YUAN Xiaojian. Simulation of temperature field in 45# steel crystallizer based on ANSYS[J]. China Foundry, 2016,65(9):879-882.

[7] HERNANDEZ-VALLE F, DIXON S. Pulsed electromagnet EMAT for ultransound measurements at elevated temperatures[J]. Insight, 2011, 53(2):96-99.

[8] 付建勋,李京社,汪春雷, 等. Q235钢杨氏模量的研究[J]. 材料导报, 2009, 23(9): 68-70.FU Jianxun, LI Jingshe, WANG Chunlei, et al. Study on Young's modulus of Q235 steel[J]. Materials Review, 2009, 23(9): 68-70.

[9] BURROWS S E,FAN Y,DIXON S. High temperature thickness measurements of stainless steel and low carbon steel using electromagnetic acoustic transducers[J].NDT and E International,2014, 68: 73-77.

[10] 杨理践, 陈俊哲, 邢燕好.基于电磁超声纵波的铝板厚度检测[J]. 仪表技术与传感器,2015,14(11):67-70.YANG Lijian, CHEN Junzhe, XING Yanhao. Thickness detection of aluminum plate based on electromagnetic ulrasonic longitudinal waves[J]. Instrum-Ent Techique and Sensor, 2015, 14(11): 67-70.

COMSOR based shear wave EMAT optimization for thicknessmeasurement of continuous casting shell

WANG Zhi-chun, YUAN Wei

(Collegeof Information Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, Inner Mongolia, China)

In order to study the mechanism and propagation of the shear wave generated by EMAT (electromagnetic acoustic transducer) in continuous casting shell, the Q235 billet with shell thickness of 10～50 mm is taken as the research object. The electromagnetic ultrasonic model of pulsed electromagnet and spiral coil is established by using the finite element software COMSOL. The distributions of electromagnetic field, force field and sound field in continuous casting slab under different EMAT parameters are analyzed. The results show that the EMAT made by the combination of the pulse electromagnet and the spiral coil can excite the ultrasonic shear wave in continuous casting shell. The effects of the coil winding number, inner radius, and radius of coils on the transfer efficiency decrease in turn. When the radius of the pulse electromagnet is larger than the size of the spiral coil, the efficiency of generating transverse wave is the highest. The smaller the thickness of the shell causes the higher the optimal excitation frequency, the higher the precision and the faster the attenuation. The frequency of 1.1 MHz is chosen as the optimum excitation frequency for the Q235 billet with the shell thickness of 10～50 mm.

continuous casting shell; electromagnetic acoustic transducer; transverse wave; thickness measurement; finite element model

TP515

A

1000-3630(2018)-03-0237-06

10.16300/j.cnki.1000-3630.2018.03.008

2017-05-25;

2017-07-18

国家自然基金项目(61463041)

王志春(1972－), 女, 内蒙古包头人, 硕士, 教授, 研究方向为电涡流无损检测和结晶器传热仿真; 电磁超声技术; 连铸坯壳测厚。

袁伟, E-mail:465895252@qq.com