炉膛声学测温中声波飞渡时间测量的实验研究

吴莉，陈励军



炉膛声学测温中声波飞渡时间测量的实验研究

吴莉，陈励军

(东南大学信息科学与工程学院，江苏南京 210096)

炉膛内温度分布的实时监测对大型燃煤锅炉的控制和诊断具有重要意义。声波飞渡时间作为声学测温方法中的重要参数，因炉膛内复杂的燃烧环境而很难精确测量。以国内机组容量为50 MW的燃煤锅炉为研究对象，分析了炉膛内背景噪声以及不同频率的单频信号在炉膛内的衰减特性，从而确定测温中的声波信号频段。并提出采用互相关时延估计法结合希尔伯特变换取包络的方法获得声波飞渡时间。实验结果表明，采用取包络的方法相比未取包络具有更高的精度和更好的稳定性。

声学测温；声波飞渡时间；衰减特性；互相关时延估计；希尔伯特变换

0 引言

在电站锅炉中，炉内温度场分布是其稳定运行和高效燃烧的重要指标之一。声学测温方法因具有非接触式测温、实时性好且能工作在恶劣的环境之下等优点[1]，近20年来，备受国内外研究者的青睐。目前在国外已经有成型的产品并且已经投入实际应用[2]，而国内该项技术尚处于基础研究和实验室研究阶段[3-4]。

声波在炉膛内飞渡时间的测量是声学测温方法的关键，但炉膛内复杂的燃烧环境(包括变化的烟气成分、微粒物质、传播路径、烟气速率等)给这一关键量的精确测量带来很大的难度。因此，炉膛内背景噪声的研究以及声波飞渡时间精确测量方法的选择尤为重要[5]。文中通过研究国内机组容量为50 MW的锅炉运行时的背景噪声和不同频率单频信号在炉膛内的衰减特性，从而确定测温的声波信号频段。此外，提出采用互相关时延估计与希尔伯特变换取包络相结合的方式获得声波飞渡时间，最后分别对取包络和未取包络的情况下获得的声波飞度时间进行了精度分析。

1 声学测温原理

声学测温是基于声波在介质中的传播速度与介质的温度有关这一原理。根据平面波的运动方程、波动方程和气体状态方程推导出声学测温的原理方程如下[6]：

图1 声波测温原理示意图

2 声波飞渡时间测量基本理论

2.1 互相关时延估计原理

互相关时延估计是利用两个空间上相互独立的信号的相关函数来估计时间延迟。

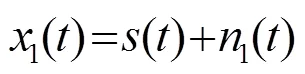
根据自相关函数性质可知：

2.2 互相关时延估计精度分析

任何时延估计方法得到的时延估计精度都受到克拉美-罗下界的限制，当输入信噪比较小时，互相关时延估计精度的最优下界表达式为[7]

2.3 希尔伯特变化原理

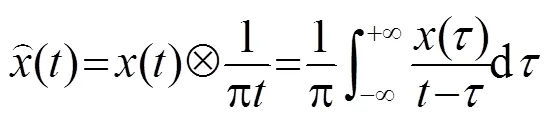
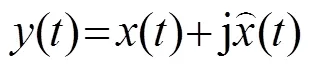
3 测温声波信号的频段选择

炉膛内的高强度噪声给声波飞渡时间的测量带来很大难度，由于声波信号的选择显得尤为重要。由于扫频信号的相关函数具有明显峰值，且可以对最大旁瓣值产生抑制，能提高飞渡时间测量的准确性[9]，所以本文采用扫频信号作为测温信号。此外，为了保证接收端可以接收到发射信号，需要对炉膛的背景噪声以及声波信号在炉膛传播过程中的衰减特性进行研究。

3.1 机组容量为50 MW的锅炉现场实验装置

在国内某电厂机组容量为50 MW的锅炉进行实验，锅炉观火孔位置分布和实验装置示意图如图2所示。在发射端，工控机控制信号发生器产生指定频率的发射信号，经过功率放大器放大后输出至固定在炉膛观火口处的扬声器，驱动扬声器发出声波信号。在接收端，传声器接收炉膛内各种声波信号，并把信号转发至多通道数据采集卡，数据采集卡由工控机控制，其采样频率为50 kHz，采样时间根据发射信号形式而改变。

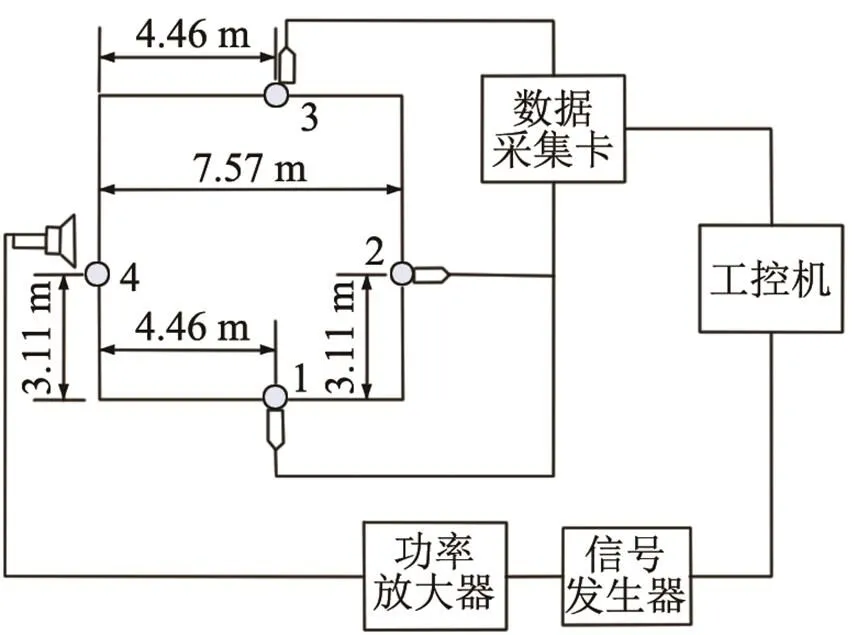
图2 现场锅炉观火孔位置分布和实验装置示意图

3.2 炉膛背景噪声研究

当锅炉运行时，炉膛内的背景噪声主要包括：燃料的燃烧噪声、吹灰器吹灰的噪声、烟气横列管束的风吹声以及其他机械噪声[10]。为确定测温信号的频带，需要先对炉膛背景噪声进行采样分析。在锅炉的某个看火口处采集噪声信号，对其分析后发现，其声压级不超过110 dB，而且频谱主要集中在1 000 Hz以下，如图3所示。此外，炉膛背景噪声的概率密度函数具有对称性，且近似为高斯分布。

3.3 声波信号在现场炉膛内的衰减特性研究

声波信号在传播的过程中，会有一定的衰减，而且频率越高，衰减越大，有效传播路径越短。通过对不同频率单频信号在炉膛中传播衰减特性的研究，结合背景噪声的特性，从而确定扫频信号的扫频区间。

在现场锅炉实验中，以锅炉的1号和3号观火孔为测点，其中一端为声波发射端，一端为声波接收端。发射端信号为1～10 kHz的单频信号，信号周期个数为300。其中，单频信号的幅度、发射端功率放大器档位保持一致。声波信号通过炉膛，在接收端采集信号。采集到的信号为发射信号衰减后信号与炉膛背景噪声信号的叠加。

图3 炉膛背景噪声声压谱级图

当单频信号的频率为1 kHz时，采集到的背景噪声和接收信号的声压谱级(参考声压为20μPa)如图4所示。由图4可知，接收信号在频率为1 kHz处有很明显的信号，其声压级为88.01 dB，信噪比约为20 dB。

图4 单频信号为1 kHz时接收信号和背景噪声声压谱级图

当单频信号的频率为2 kHz时，采集到的背景噪声和接收信号的声压谱级(参考声压为20μPa)如图5所示。由图5可知，接收信号在频率为2 kHz处的信号声压级为75.57 dB，信噪比也约为20 dB。

当单频信号的频率为3 kHz时，采集到的背景噪声和接收信号的声压谱级如图6(a)所示。由图6(a)可知，接收信号在频率为3 kHz处的信号相比图4、图5有所减弱，对其局部放大后得图6(b)，此时3 kHz处的信号的声压级为53.32 dB，信噪比约为15 dB。

当单频信号的频率分别为4 kHz、5 kHz时，其对应的背景噪声和接收信号的声压谱级图的局部放大图如图7、8所示。由图7和图8可知，此时接收信号中单频信号强度较小，信噪比也比较低。当单频信号的频率为5 kHz时，接收信号在5 kHz处的信噪比最大约为3 dB。

图5 单频信号为2 kHz时接收信号和背景噪声声压谱级图

图6 单频信号为3 kHz时接收信号和背景噪声声压谱级图及局部 放大图

当单频信号频率大于5 kHz时，接收信号中正弦信号几乎完全淹没在噪声中，图9为单频信号频率为6 kHz时，接收信号和背景噪声声压谱级局部放大图。

图7 单频信号为4 kHz时接收信号和背景噪声声压谱级局部放大图

图8 单频信号为5 kHz时接收信号和背景噪声声压谱级局部放大图

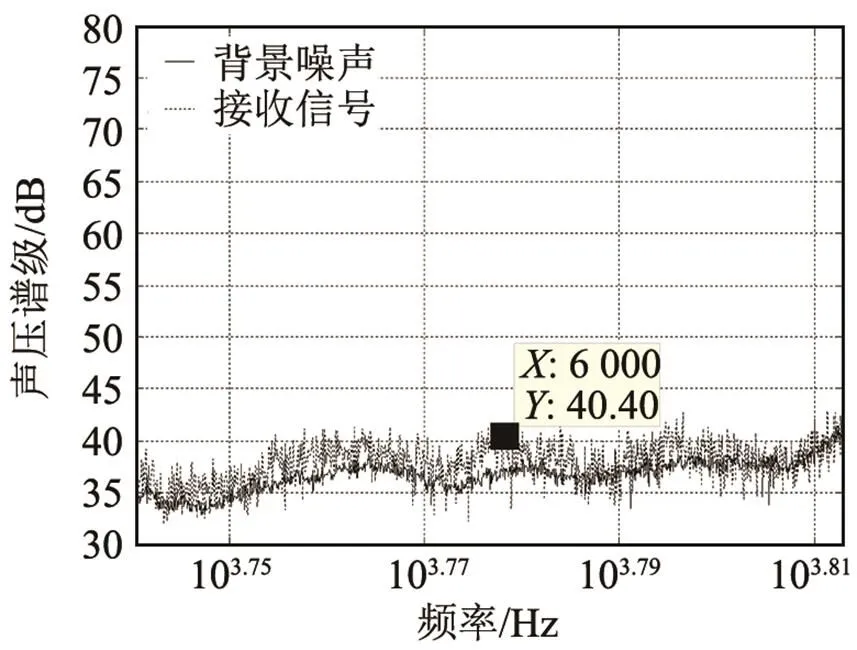
图9 单频信号为6 kHz时接收信号和背景噪声声压谱级局部放大图

根据现场的试验测量，炉膛内温度为1 200 ℃，声波飞渡时间为10 ms。若采用互相关时延估计法测量声波飞渡时间，在理论上只会产生0.03 ℃的温度误差。由此可见，采用互相关时延估计法来估计声波飞渡时间，理论上可以得到非常高的估计精度。

4 数据处理和分析

首先根据发射信号的频率间隔，对接收信号进行带通滤波处理。带通滤波器的滤波区间为950～3 050 Hz，阶数为1 024阶。此时，滤波后产生的群时延为

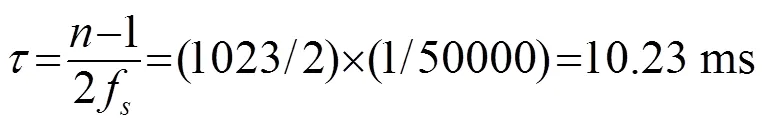
为得到更加准确的结果，在计算声波飞渡时间时，需要剔除滤波器带来的群时延。

对滤波后的接收信号与发射信号做互相关运算，图10和图11分别为2号观火孔处的120帧信号与发射信号之间的互相关函数历程图和互相关函数包络历程图及局部放大图。

从图11(a)可以看出，互相关函数包络历程图中存在一个由直达波形成的清晰且稳定的互相关峰和一个由炉墙反射产生的多条传播路径形成的较微弱的互相关峰。

由图10(b)可知，未取包络的互相关函数历程图中存在两个清晰且稳定的峰值和一个清晰的负峰值。为进一步验证多峰确实存在，取图10(b)中某一帧信号得到图12。从图12中可以看出，此时互相关函数中确实存在多个峰值点。相比之下，取包络后的互相关函数历程图的峰值点较为单一和稳定。

图13为互相关函数取包络和未取包络时得到的时延估计分布图。统计得到两种情况下的时延估计均值均为12.1 ms。但是，从图中可以看出，互相关函数未取包络时，时延估计值在两个时延点处均匀地跳变。而互相关函数取包络时，时延估计值则相对稳定。统计得到互相关函数未取包络时的时延估计均方差为3.300 5×10-4s，而互相关函数取包络时的时延估计均方差仅为1.732 0×10-4s。令炉膛内的温度为1 200 ℃，互相关函数未取包络时，时延估计均方差对应的温度均方差为32.7 ℃，而互相关函数取包络时，时延估计均方差对应的温度均方差仅为17.18 ℃。可见，互相关函数取包络后时延估计值较为稳定，这对实时测量炉膛内的温度场分布具有重要意义。

图10 互相关函数历程图及其部放大图

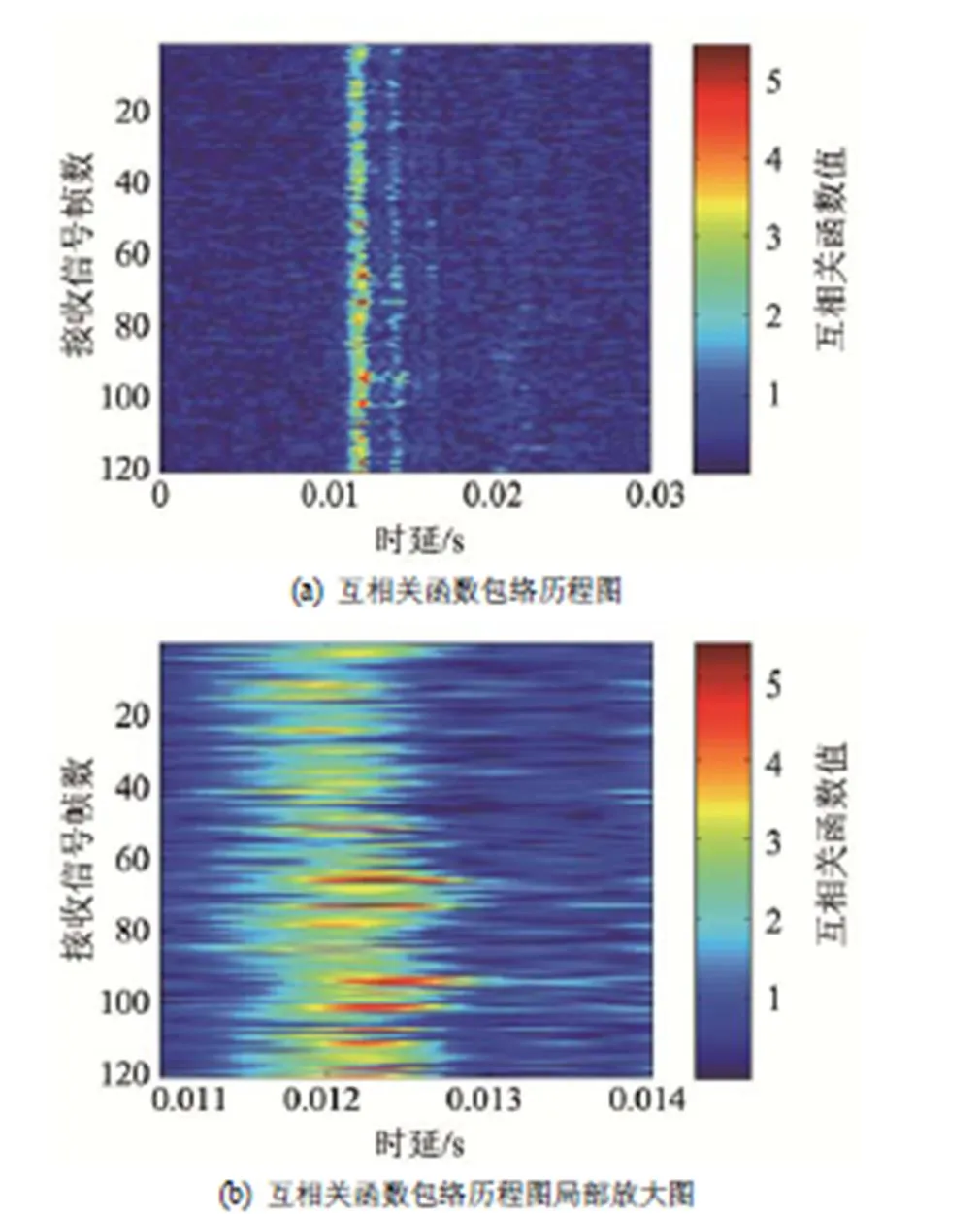
图11 互相关函数包络历程图及其局部放大图

Fig.12 互相关历程图中一帧信号图

图13 互相关函数取包络和未取包络时延分布图

5 结论

(1) 机组容量为50 MW的锅炉炉膛的背景噪声声压级在110 dB以下，频谱主要集中在 1 kHz以下。噪声概率密度函数具有对称性，近似为高斯分布。

(2) 炉膛声波衰减特性测试实验分析结果表明：当信号频率小于3 kHz时，衰减较小；当信号频率大于3 kHz时，衰减急剧增大；当频率大于5 kHz时，声波信号几乎全部淹没在背景噪声中。本文采用扫频区间为1～3 kHz的线性扫频信号作为声波发射信号。

(3) 炉膛声波飞渡时间的测量结果表明，接收与发射信号互相关函数历程图中有多个峰值点。为减小多峰带来的误差，本文提出采用互相关时延估计法与希尔伯特变换取包络相结合的方法计算炉膛内声波的传播时间，即声波飞渡时间。实验结果表明，互相关函数取包络相比互相关函数未取包络可以获得更加稳定且准确的声波飞渡时间，这对声学法测量锅炉炉膛内的温度场分布具有重大意义。

[1] SHEN Guoqing, ZHANG Shiping, AN Liansuo. Study on Sound Source in Acoustic Pyrometry of Boiler Furnace[J]. Electric Power Science and Engineering, 2013, 29(2): 49-55.

[2] KLEPPER J A, RENO N V. Method and apparatus formeasuring acoustic wave velocity using impulse response[J]. J. Acoust. Soc. Am., 1994, 98(1): 27-28.

[3] 田丰, 邵富群, 王福利. 基于声波的工业炉温度场测量技术[J]. 沈阳航空工业学院学报, 2001, 18(3): 10-11.

TIAN Feng, GUO Fuqun, WANG Fuli. Industrial furnace temperature field measurement technology based on sound waves[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2001, 18(3): 10-11.

[4] 姜根山, 安连锁, 杨昆. 温度梯度场中声线传播路径数值研究[J]. 中国电机工程学报, 2004, 24(10): 210-214.

JIANG Genshan, AN Liansuo, YANG Kun. Numerical study on the propagation path of sound ray through the temperature grandient field[J]. Proceedings of the CSEE, 2004, 24(10): 210-214.

[5] 安连锁, 张世平, 李庚生, 等. 电站锅炉声学监测中互相关时延估计影响因素研究[J]. 动力工程学报, 2012, 32(2): 112-117.

AN Liansuo, ZHANG Shiping, LI Gengsheng, et al. Factors influencing cross-correlation time delay estimation of acoustic measurement for power boilers[J]. Journal of Chinese of Power Engineering, 2012, 32(2): 112-117.

[6] KLEPPE J A. The application of digital signal processing to acoustic pytometry[J]. IEEE, 1996, 520-422.

[7] 苗锦, 刘志强, 张跟鹏. 基于互相关时延估计方法及其精度分析[J]. 舰船电子工程, 2008, 28(6): 98-100.

MIAO Jin, LIU Zhiqiang, ZHANG Genpeng. Cross correlation method and precision analysis of time-delay estimation[J]. Ship Electonic Engineering, 2008, 28(6): 98-100.

[8] 管致中, 夏恭恪, 孟桥. 信号与线性系统上册[M]. 北京: 高等教育出版社, 2008.

GUAN Zhizhong, XIA Gongke, MENG Qiao. Signals and linear systems[M]. Beijing: Higher Education Press, 2008.

[9] 张波, 安连锁, 沈国清. 互相关函数在声学测温系统中的误差分析[J]. 电子科学与工程, 2006(1): 45-47.

ZHANG Bo, AN Liansuo, SHENG Guoqing. Error analysis of acoustic pyrometer based on cross-correlation method[J]. Electric power science and engineering, 2006(1): 45-47.

[10] 张世平, 安连锁, 沈国清. 电站锅炉声学测温中炉膛声场及热态背景噪声特性研究[J]. 华北电力大学学报, 2011, 38(6): 68-74.

ZHANG Shiping, AN Liansuo, SHEN Guoqing. Study on characteristic of sound field and hot-state background acoustic noise in boiler furnace of acoustic pyrometry[J]. Journal of North China Electric Power University, 2011, 38(6): 68-74.

Experimental research on ‘time of flight’ measurement inacoustic pyrometry for furnace

WU Li,CHEN Li-jun

(School of Information Science & Engineering, Southeast University, Nanjing 210096, Jiangsu, China)

Real-time monitoring of the temperature distribution is of great significance to the control and diagnosis of large coal-fired boilers. Time of flight (TOF) as an important parameter of acoustic pyrometry is difficult to measure in the complex combustion furnace environment. In this paper, the coal-fired boiler of 50 MW unit capacity is taken as the research object. The background noise and the attenuation characteristics of the single-frequency signals with different frequencies in the furnace are analyzed to determine the frequency band of the acoustic signal in the temperature measurement. And, the cross-correlation time delay estimation method combined with the Hilbert transform for envelope extraction is used to obtain the time of flight (TOF). The experimental results show that the proposed method has better accuracy and stability over the non-envelope extraction method.

acoustic pyrometry; time of flight; atenuation characteristics; Hilbert transform

TB533

A

1000-3630(2018)-03-0211-06

10.16300/j.cnki.1000-3630.2018.03.003

2017-05-04;

2017-07-18

吴莉(1990－), 女, 江西抚州人, 硕士研究生, 研究方向为信号与信息处理。

吴莉, E-mail: wuli199909@163.com