基于ACO算法的危险化学品车辆运输路径优化方法*

徐少甫， 陈家晨， 胡莹石， 方宁生

(1.江苏省物联网应用技术重点实验室，江苏 无锡 214064;2.无锡太湖学院 计算机应用与外语学习中心，江苏 无锡 214064;3.东南大学 计算机科学与工程学院，江苏 南京 210000)

危险化学品通过不同模式运输，危险大部分(超过80%)都发生在公路上[1].因此，需要合理规划公路运输路线，以此减少运输危险化学品造成的公共风险.目前，有学者已经提出了多种求解模型，一些是使用单目标路径优化算法，将最短路径确定为最佳路线，或以最小化给定起点-目的地的风险作为目标[2-5].然而，在许多实际应用中(如气瓶的运输)，危险品的运输要求一组卡车来同时服务一组客户.另外，为了获得更好的路线，需要考虑多种目标因素，即同时考虑运输风险和运输成本[6].一些学者利用混合整数线性规划(MILP)方法[7]进行路线求解，但这种方法中扫描解空间的量是巨大的，有时无法在多项式时间内计算.元启发式技术能够在适度的计算时间内生成解决方案，通过使用复杂的进化程序对解决方案空间中最佳区域进行探索，获得的解决方案具有更高质量.常用的智能优化算法有遗传算法、粒子群算法、蚁群算法和蜂群算法等[8]，其中蚁群算法具有较快的收敛速度且能避免陷入局部最优等优点[9].

为此，综合考虑运输风险和运输成本来构建目标函数，通过蚁群优化(ACO)算法来获得最优运输路线.仿真中将本文方法与MILP进行了比较，结果证明了本文方法的有效性和可行性.

1 运输问题模型

本研究的问题可以定义为确定一组携带危险品的车辆的帕累托最优路线，以满足给定一组客户的需求问题.其中具有以下约束条件：路径选择必须是多目标的，并且应该作为一个单步过程来执行；尽量减少总的预定行程时间以及路线的总风险值，这是路线规划中最小化的两个主要目标；所有车辆必须在仓库站点出发；车辆开始和结束操作的时间必须在仓库指定的时间范围内；客户的需求必须在预先规定的时间范围内满足.

1.1 运输风险计算

运输中的风险区别于其他运输问题，其直接影响生命安全.因此，风险最小化是主要目标之一.学者已经进行了充分的研究，努力获得更好的定性和定量风险模型.考虑到在道路链路l上发生事故H，该事故可以由O类型泄漏事故，U类型交通事故和人口受伤后果D联系起来. 因此，与道路链路l相关的总运输风险Rl可表示为：

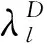
1.2 目标函数

2 蚁群优化算法

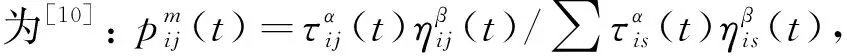
3 基于ACO的运输路径优化

本文利用ACO来获得最优的运输路线.但是，为了利用所有基于运输时间和风险目标的非支配路径进行路径选择和单步优化，所提出的算法还包括局部搜索步骤以提高帕累托最优解的质量.在进行解决方案构建步骤之前，在所有客户和仓库节点执行标签算法以获得集合P，从而获得集合N.集合P包括用于路径选择的所有路径.ACO中的蚂蚁使用这些路径来构建它们的路线(解决方案).采用局部搜索方法来提高每次迭代中构建的解决方案的质量.ACO运输路径优化算法的流程如算法1所示.

算法1:ACO运输路径优化过程步骤1:在所有节点(客户和仓库)执行标记算法以找到集合P,并且定义G(N,L).步骤2:设置参数.使用最近的邻域搜索,基于初始解初始化路径信息素值和Pareto最优集合S.对于迭代次数n = 1,根据信息素的值来初始化N中所有链路的信息素值.步骤3:For蚂蚁编号m=1 to M3.1:设置车辆数K = 1,将蚂蚁放在仓库节点,其中i = 0.3.2:从i中识别可行的客户节点集合,即N',设定一个将i连接到N'的链路L'集合.如果N'为空,则添加从i到仓库节点的所有链路到L'中.3.3:从L'中选择一个链路i,j . IF已被利用,选择具有最大启发式和信息素值的链路i,j . Else,使用选择概率随机选择.3.4:所选链路i,j 的信息素值进行局部更新.3.5:IF与选定链路i,j 对应的节点是仓库节点,则设置K =K +1,i = 0. Else,设置i =与选定i,j 对应的客户节点.3.6:IF有更多的客户需要服务,则转到步骤3.2.3.7:设定总车辆= K-1.步骤4:IF m<蚂蚁总数M,m= m+1并转到步骤3.步骤5:根据优势规则更新S.步骤6:将本地搜索应用于S中的每个解决方案.步骤7:根据当前S的平均目标函数值查找新的跟踪信息素值.步骤8:IF之前的路径信息素值<新的路径信息素,则设置当前路径的信息素值=新的路径信息素,并初始化L中所有链路的信息素值.Else,对属于S中解的所有链路i,j 进行信息素的全局更新.步骤9:迭代次数n=n+ 1,转到步骤3,直到n=最大迭代次数Nmax.

4 仿真分析

测试实例是一个现实中的道路网络数据，网络中有225个节点和781个链接.每条单向道路用单向链路建模，每条双向道路由两个单向链路建模.在网络中的225个节点中，有8个客户节点和1个仓库节点.客户节点编号分别为1、7、8、13、18、20、22和24；仓库节点编号为17. 客户的时间窗口是随机生成的，每个客户假定需求量为3 300 L化学品.设置车队有2辆卡车同时运输，所有车辆均具有20 000 L的容量.

在配备Intel i5-7500 CPU，8 G内存的PC机上，通过MATLAB R2014软件执行优化算法.所有链接都在GIS地图中进行识别，以确定该地区人口的地理分布.此人口数据用于计算实例中每个链接的相关风险.对于ACO算法中参数，设置α=10，β0=1，ρ0=0.1，Nmax=200.

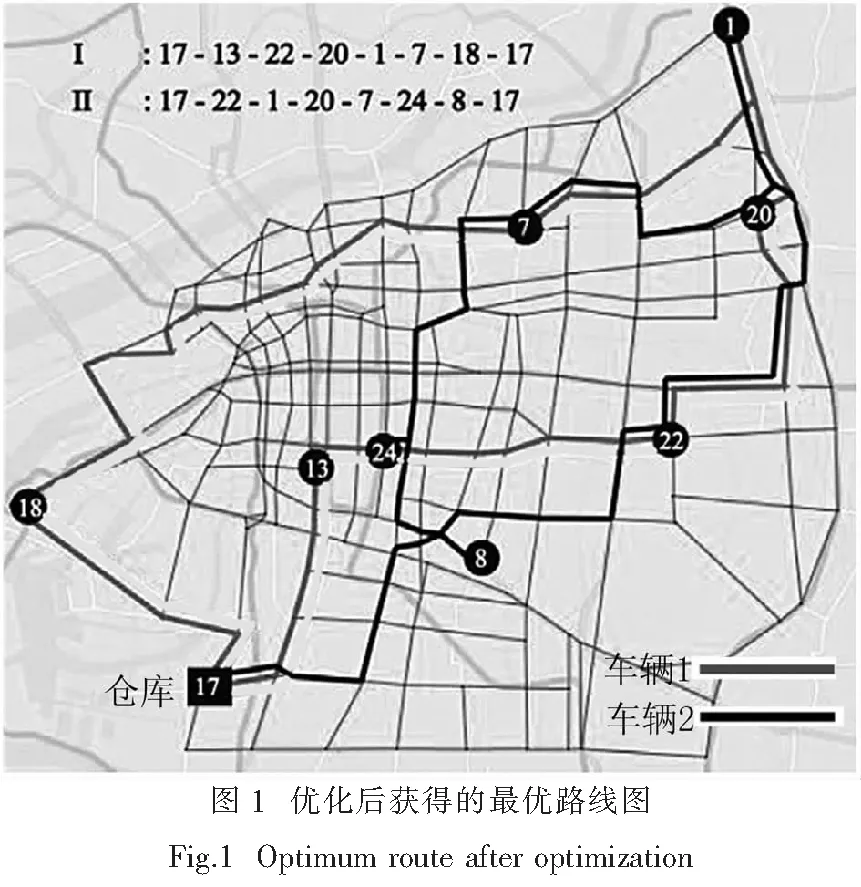
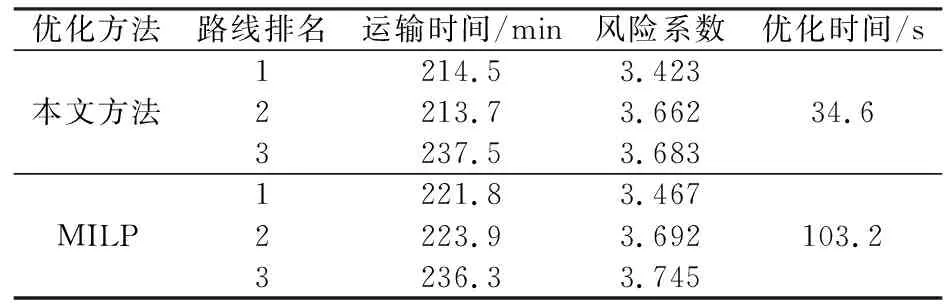
表1 排名前3的路线指标

优化方法路线排名运输时间/min风险系数优化时间/s本文方法1214.53.4232213.73.6623237.53.68334.6MILP1221.83.4672223.93.6923236.33.745103.2

实例中的道路网络、客户和仓库的位置，以及通过本文方法优化后获得的最优路线如图1所示.从图1可以看到，车辆1的路线为17-13-22-20-1-7-18-17，车辆2的路线为17-22-1-20-7-24-8-17.由于城区人口密集，这些路线都避开了城区核心区域.

另外，将本文方法与混合整数线性规划(MILP)方法进行比较，表1给出了两种方法获得的排名前3的路线的总体指标.可以看到，本文方法的优化结果中，最优线路的运输时间为214.5 min，风险系数为3.423.其运输时间与线路2的运输时间213.7 min近乎一致，但风险系数比线路2的3.662有明显减小.这是因为本文优化目标中对风险系数的权重较大，而对运输时间的权重较小，只有在保证运输安全的前提下才会进一步缩短运输时间.与MILP方法的对比可以看到，本文方法获得的路线在运输时间和风险系数上都较优，且优化时间只需要35 s，比MILP有明显提升.这是因为MILP是一种遍历搜索过程，需要遍历所有解空间，耗时较长.而本文采用了ACO智能优化算法能够快速收敛到最优解.