具有定常输入的二阶多智能体系统的平均一致性滤波

郑敏，刘成林，刘飞

（江南大学 自动化研究所，江苏 无锡 214122）

目前，多智能体系统的分布式协调控制引起了众多学者的关注，并得到了广泛应用。一致性问题是多智能体系统协调控制的最简单与最基本问题之一，得到了非常深入的研究，并取得了广泛的研究成果。

近些年，一致性滤波问题[1]引起了部分学者的研究兴趣，并在分布式估计、分布式传感器网络等领域得到应用。一致性滤波问题是指基于一致性协调控制的滤波算法，使每个智能体通过和相邻智能体之间进行信息通信来达到相同的状态；如果每个智能体渐近收敛到给定输入的平均值，那么这就是平均一致性滤波问题[2]。Olfati-Saber等[3-5]分别提出了分布式低通一致性滤波和高通一致性滤波，它们通过追踪网络中所有智能体输入的平均值来实现一致性滤波，但是存在估计误差。针对文献[3-5]中算法存在的误差，涌现了一些改进算法来减少估计误差[6-9]。Freeman等[7]提出了比例积分算法(proportional-integral algorithm)，证明了该算法在输入是常量的情况下收敛一致。与文献[7]相比，Bai等[8]运用内部模型原则[10]设计传递函数使每个智能体跟踪所有时变输入的平均值。Li等[11]对比例积分算法(PI)进一步研究，提出了改进的PI算法，并证明该算法收敛到定常输入的加权平均值；同时，Li等[12]也提出一种新的混杂一致性滤波协议，给出了该协议分别在固定拓扑和切换图下渐近一致的条件。

实际上，在多智能体协调控制网络中，智能体之间进行信息传输伴随着通信时延，会影响系统集体行为。目前，具有通信时延的一阶和二阶多智能体系统的一致性问题受到了学者的广泛关注[13-18]。Olfati-Saber等[19]考察了具有通信时延的一阶多智能体系统的一致性问题，给出了在相同通信时延作用下多智能体系统收敛一致的时延范围。Wang等[20]基于圆盘定理和最大模原理，给出了智能体在具有不同通信时延的一阶多智能体系统达到渐近一致的收敛条件。Lin等[21]分析了具有相同时延的二阶多智能体系统的一致性问题，给出了一致性收敛的时延相关充要条件。针对具有不同时延的二阶多智能体系统的一致性问题，Yang等[22]根据小增益稳定性原理，分别得到具有时不变和时变通信时延的系统渐近达到一致的充要条件，并把结论运用到时延高阶多智能体系统的一致性分析中。

本文研究具有定常输入的二阶多智能体系统的平均一致性滤波问题。在现有的一致性滤波算法基础上，提出了一种比例积分算法(PI)，并考察多智能体系统在定常输入和对称连通拓扑结构下的收敛问题。利用Routh判据，得到二阶多智能体系统渐近达到平均一致滤波的重要条件；根据Nyquist判据，分析了二阶多智能体系统在相同通信时延约束下渐近收敛平均一致滤波的充分条件。

1 问题描述

1.1 连接拓扑图

n 阶 有向图 G =(V,E,A)的组成部分包括：节点集V={v1,v2,···,vn}、 边集 E ⊆ V ×V以及加权邻接矩阵A=[aij]∈ Rn×n。便于描述，节点的下标集表示为Γ ={1,2,···,n}。 在图 G 中 ，节点i指 向节点 j的有向边为eij=(i,j)∈E ， 对应的连接权值为 aij＞0，否则，aij=0 。 如果 aij=aji＞0 ， 则称图 G 是对称的。节点i的邻接集合定义为 Ni={j∈V:(i,j)∈ E}。根据邻接矩阵写出拉普拉斯矩阵 L =[lij](L ∈ Rn×n)，定义为

在图 G 中，若节点i和 节点 j之间有一条路径，那么称节点 j和 节点i之间是可达的，若有一个节点从图 G 中任意其他点是可达的，那么称该节点是全局可达点。若图 G 中包含全局可达点，那么该图是连通的。

在本文中， I ∈ Rn×n表 示 n 阶 单位矩阵，0n×n∈ Rn×n表示 n阶零矩阵， 1n表 示向量 [1 ···1]∈ Rn， 0n表示向量[0 ···0]∈ Rn。

1.2 模型描述

n个二阶智能体构成的二阶多智能体系统为

式中： xi∈R、 vi∈R、 ui∈R 分 别表示智能体i的位置、速度和控制输入。每个智能体有一个定常输入为φi∈ R，如果：则称多智能体系统式(1)解决平均一致滤波问题。

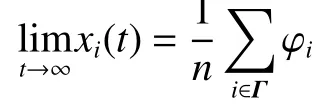
为解决二阶多智能体系统的平均一致滤波问题，本文提出了比例-积分一致性滤波算法，即

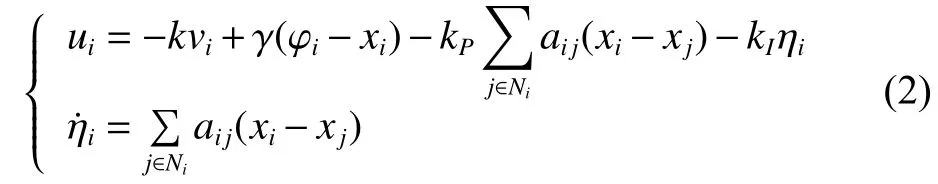
式中： φi∈ R 和 ηi∈ R 分 别表示智能体i的输入和内部状态； k ∈R 、 γ ∈R 、 kp∈R 和 kI∈R为控制常数。不同于针对一阶多智能体系统的平均一致滤波问题所提出的比例-积分一致性算法，本文直接采用一致性协调控制项的积分量 ηi加入控制算法中。

在式(2)作用下，系统式(1)的闭环形式为

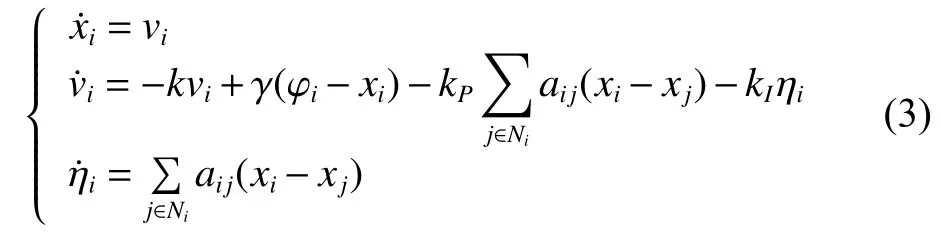
2 一致性收敛分析

2.1 无时延情况

将式(3)表示为多变量形式

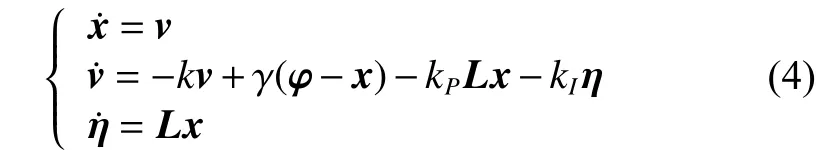
将式(4)进行Laplace变换，可得

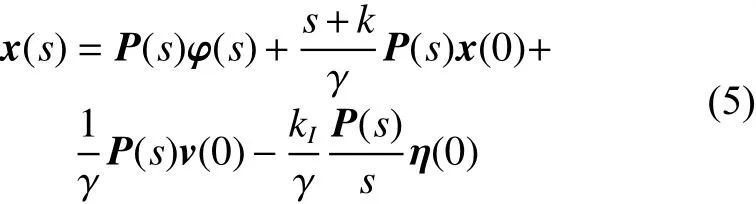
其中

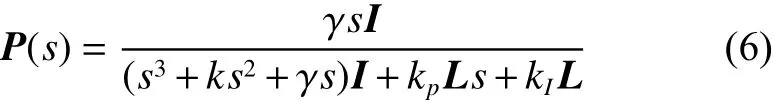
x(s)=[x1(s)x2(s)···xn(s)]T，v(s)=[v1(s)v2(s)···vn(s)]T，v(0)、 η (0)分别为智能体的位置、速度和内部状态初始值。

1) k ＞0,γ ＞0；

2)kI＞ 0,k(γ+kpλi)＞ kIλi成立，其中， λi是拉普拉斯矩阵L的特征值，并且0 =λ1＜ λ2≤ λ3≤ ···≤ λn。

证明 证明过程分两步。1) 利用Routh判据给出满足传递函数矩阵(6)特征方程的根在左半平面的条件；2) 利用传递函数的终值定理来证明多智能体系统式(3)渐近达到平均一致性。

1) 令传递函数矩阵 P (s)的特征方程为

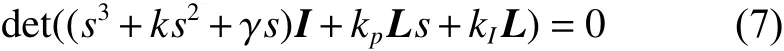
等价于

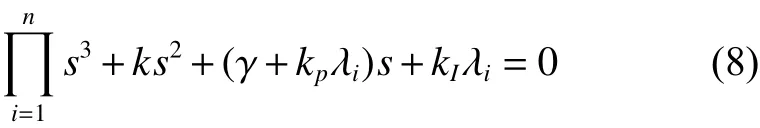
接下来，考察方程(9)的根的分布：

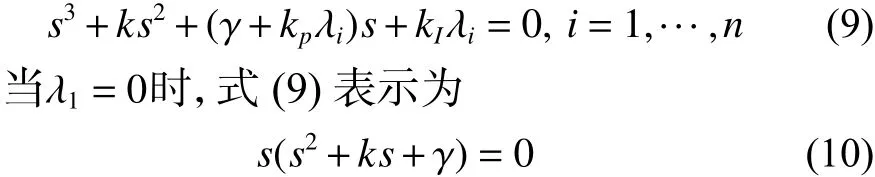
根据定理1的条件1)可得：特征方程式(10)有一个根 s =0，并且其他根为负实数。

当λi,i=2,3,···,n时，方程(9)的Routh阵列表为

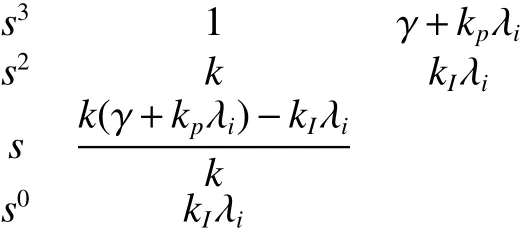
当且仅当定理1中的条件1)和2)都成立，Routh阵列表第一列系数为正数，特征方程式(9)的根是负实数。

因此，当且仅当定理1的条件1)和2)都成立时，多智能体系统式(3)渐近达到一致，则c，其中c为常向量。

2)为了证明多智能体系统式(3)渐近达到平均一致滤波，分别证明式(5)满足：

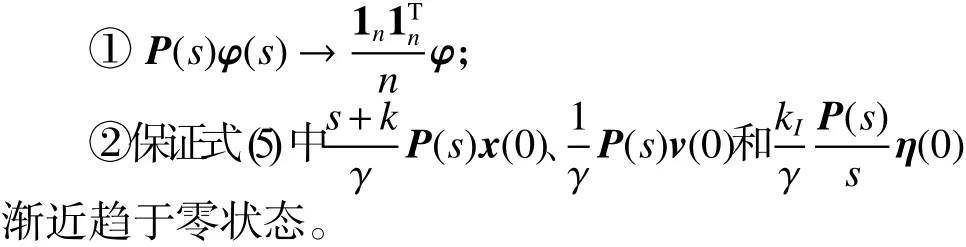
①的证明 在无向连通拓扑结构下，Laplacian矩阵 L 是实对称的。 λ1=0 是 L 的一个单一特征值，对应的右特征向量为他 n −1个特征值对应的特征向量为则 Q QT=I， Q LQT=diag{λ1,···,λn}。

通过计算，可得

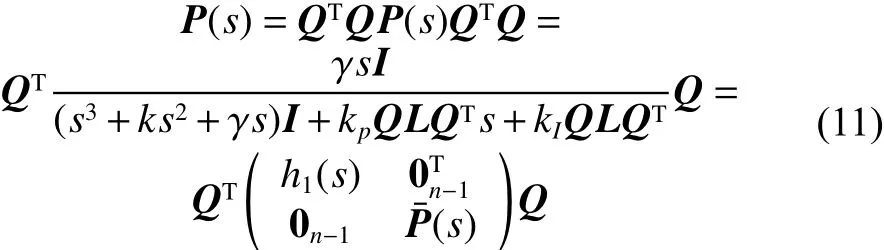
式中

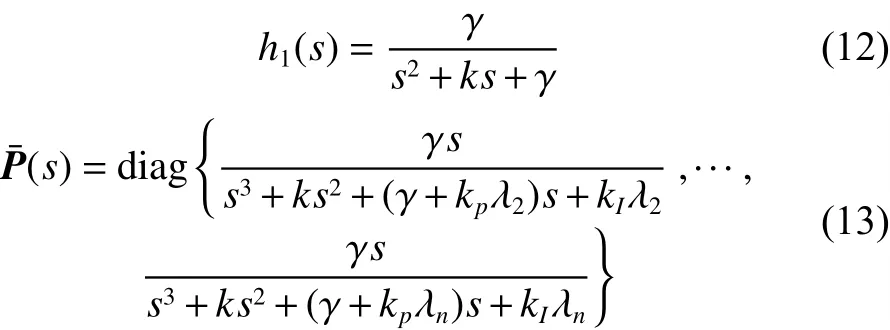
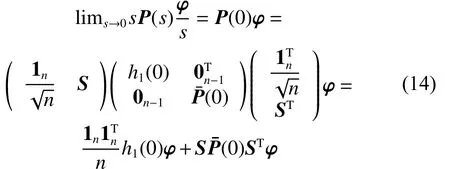
根据终值定理可得h1(0)=1¯P(0)=diag{0,0,···,0}

②的证明 由①的证明可得：

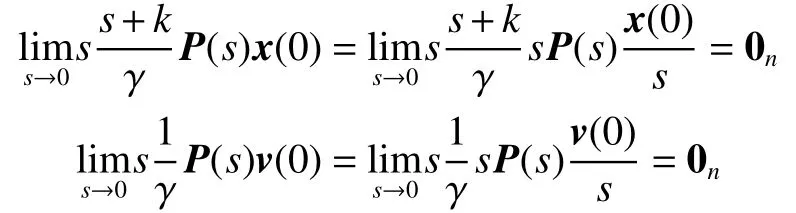
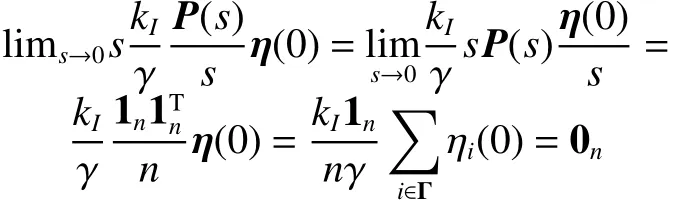
综合证明①和②，可以得到limt→∞xi(t)=即多智能体系统式(3)渐近达到平均一致滤波。

2.2 有时延情况

由于通信时延在多智能体系统协调控制中不可忽略，接下来考察式(2)在相同通信时延约束下的收敛问题：

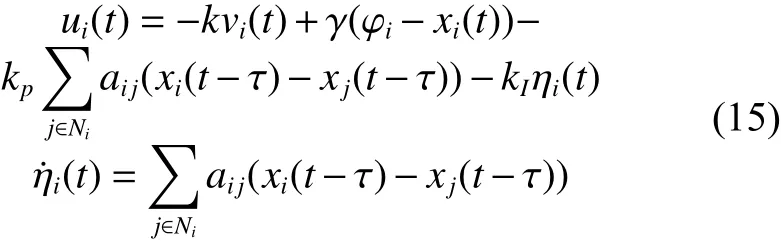
在式(15)作用下，多智能体系统式(1)的闭环形式为

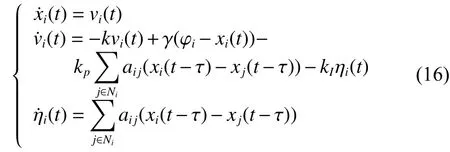
式中通信延时 τ ＞0。对式(16)进行Laplace变换得到

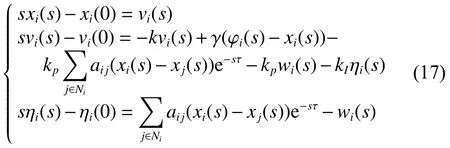
式中

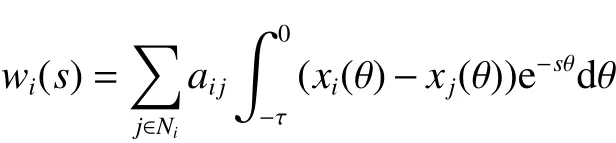
定义一个向量w (s)=[w1(s)w2(s)···wn(s)]T，式(17)可进一步描述为

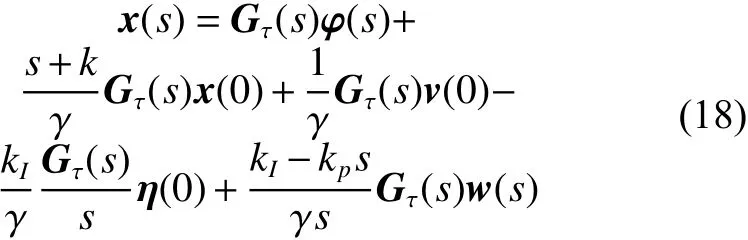
式中

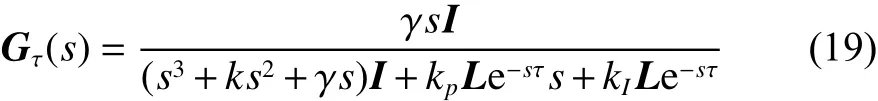
定理2 假设多智能体系统式(16)的连接拓扑为对称连通的。参数 k、γ、 kp、kI满足定理1给出的条件，且(16)渐近达到平均一致滤波，如果条件：多智能体系统式

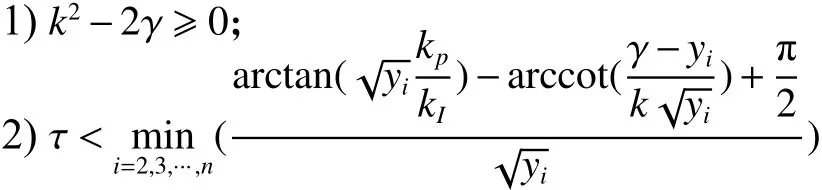
成立，其中 yi是式(20)的唯一正根：

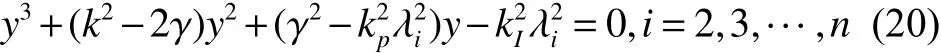
在证明定理2之前，先给出2个有用的引理：引理1 考察函数：

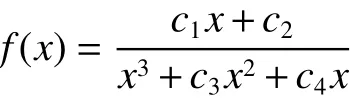
假设满足 c1＞0 、 c2＞0 、 c3＞0 和 c4＞0，那么在区间x∈(0,+∞)上 f (x)是单调下降的。

证明 对 f (x)关 于 x的导数：

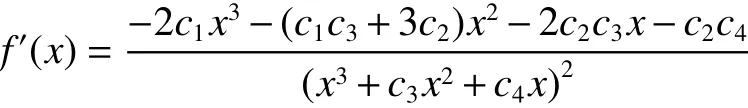
由于 c1＞0 、 c2＞0 、 c3＞0 和 c4＞0，那么在区间x∈(0,+∞)上 f′(x)＜ 0始终成立，因此可得在区间x∈(0,+∞) 上 f( x)是单调下降的。

引理2 考虑3次多项式：

假设满足系数 d1≥0并 且 d3＜0，根据韦达定理，满足f1(x)=0只有唯一正根。

定理2证明 证明过程分两步。1)利用频域分析方法来给出使系统式(16)渐近达到平均一致滤波的通信时延 T 的范围；2)利用终值定理证明多智能体达到平均一致性滤波。

1)根据式(19) Gτ(s)特征方程为

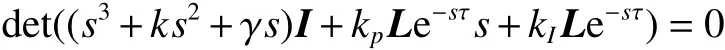
等价于

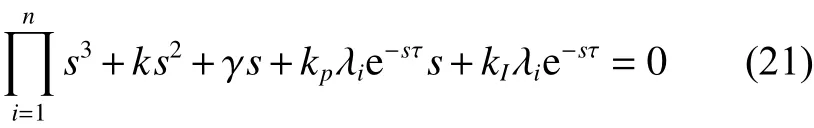
考察方程式(22)的根：

当 s =0时，特征方程式(22)变为

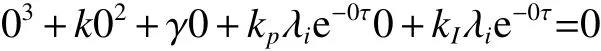
满足 kIλi=0 ， 由于 λ1=0 ， 所以满足 λ1=0 时 ， s =0是特征方程的单根。

当 s ≠0时，式(22)整理为闭环特征函数的形式：

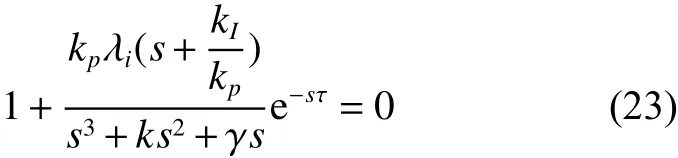
开环特征函数为

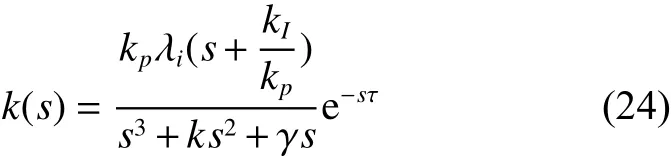
当 s =jw，开环特征函数式(24)的频率特性为

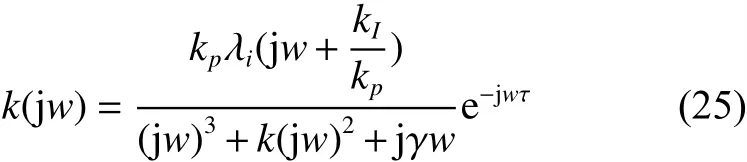
根据Nyquist判据，特征方程(22)的根是负实数，等价于 k (jw)的 Nyquist曲线不包围 (− 1,j0)点。整理式(25)可得幅频特性为

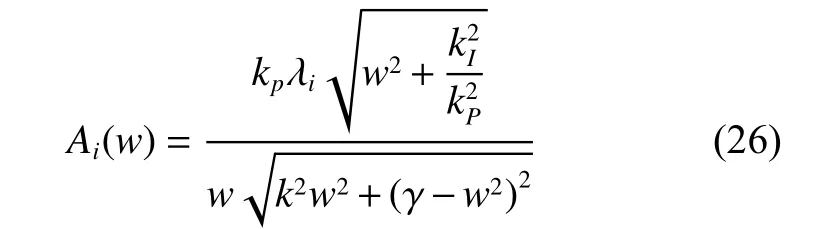
相频特性为

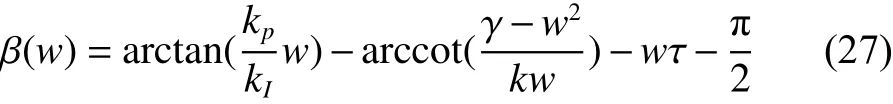
接下来，考察 Ai(w)关 于 w 的 单调性。令 w2=y，考察函数

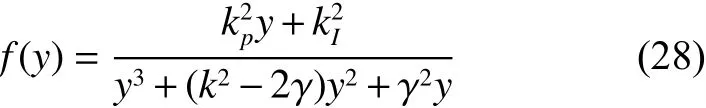
由于k2−2γ ≥0， 根据引理1可得 f (y)在 区间y∈(0,+∞)上 是单调下降的函数，即幅频特性 Ai(w)随 着 w的增大而下降。令 Ai(w)=1 ， 即f(y)=1 ，可得

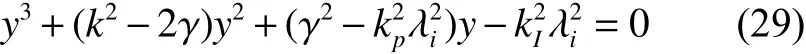
由于k2−2γ ≥0， 根据引理2，方程式(29)在y∈(0,+∞)只 有一个正解 yi， 即 Ai(w)=1 ，在 w ∈(0,+∞)的解可 知，λi关 于 f (yi)是单调下降的，根据 f (yi)关 于 yi是 单调下降的，因此 λi关 于 yi是单调上升的。根据Nyquist判据，为了使 k (jw)奈奎斯特图不包围 (− 1,j0)点 ，当幅值 Ai(w)=1时，对应求得的相频特性满足

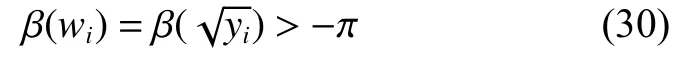
由式(27)得

因此，当条件1)和2)成立时，特征方程式(22)的根满足： s =0为单根，非零根均具有负实部。

2)根据定理1中①的证明，可得

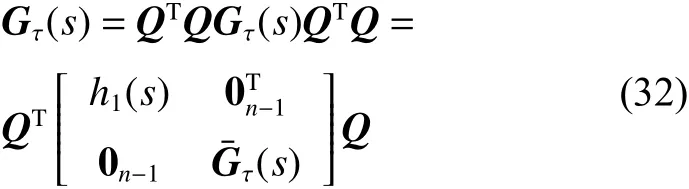
式中

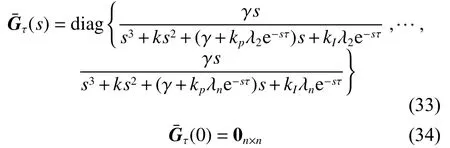
根据 h1(0)=1，并结合式(32)和式(34)可得

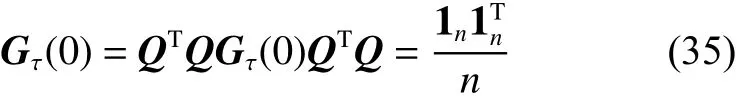
根据终值定理

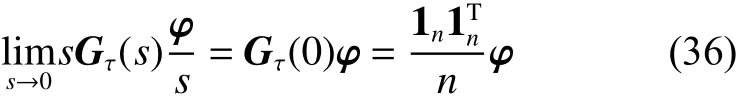
与定理1的②的证明类似，式(18)运用终值定理，可得

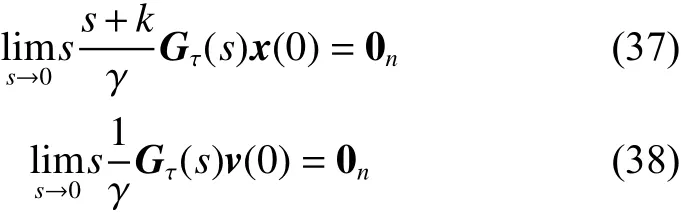
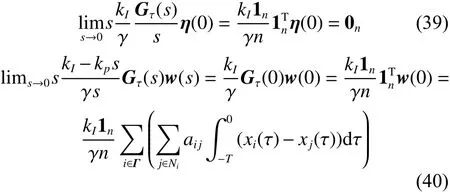
由于 aij=aji，得到

因此

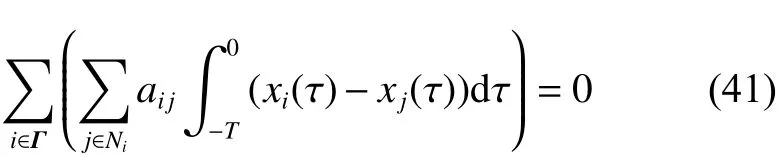
根据式(41)，式(40)可以进一步表述为

根据定理2的证明，如果条件1)成立， λn≥ λi，yn≥ yi,i=2,3,···,n−1显然成立。在条件1)和2)成立的前提下，如果式(27)中 β (w)在 w ∈[+∞)区间上单调减，则条件2)给出的时延条件为充分必要的。

3 数值仿真

3.1 无时延的二阶多智能体系统

考察由5个智能体构成的多智能体系统，其拓扑结构是无向连通的(见图1)。在连接拓扑中，智能体之间的连接权值是对称的，分别为：a12=a21=1，a15=a51=1， a23=a32=1，a34=a43=1， a45=a54=1。计算可得，拉普拉斯矩阵 L 的特征值为：λ1=0,λ2=1.382,λ3=1.382,λ4=3.618,λ5=3.618。

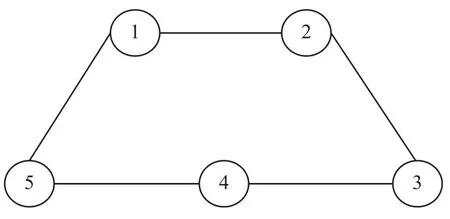
图1 包含4个多智能连接拓扑GFig. 1 Graphical topology of four agents

随机设定智能体初始位置和初始速度，且内部状态的初始值设为 η (0)=[2−1−3 2 0]T，满足智能体的常量输入为： φ =[8−2−20 1]T，则定常输入的平均值为数分别为： k =1、 r =0.3、 kp=0.4。根据定理1，可得0＜kI＜0.483 。 当 0 ＜kI＜0.483时，智能体的位置轨迹渐近达到所有常量输入的平均一致和速度轨迹趋于零，如图2所示。当 kI≥0.483时，智能体的位置和速度发生振荡(kI=0.483 ) 如图3所示或发散(kI＞0.483)如图4所示。

图2 智能体的位置和速度(k I= 0.03)Fig. 2 Positions and velocities of agents with k I= 0.03

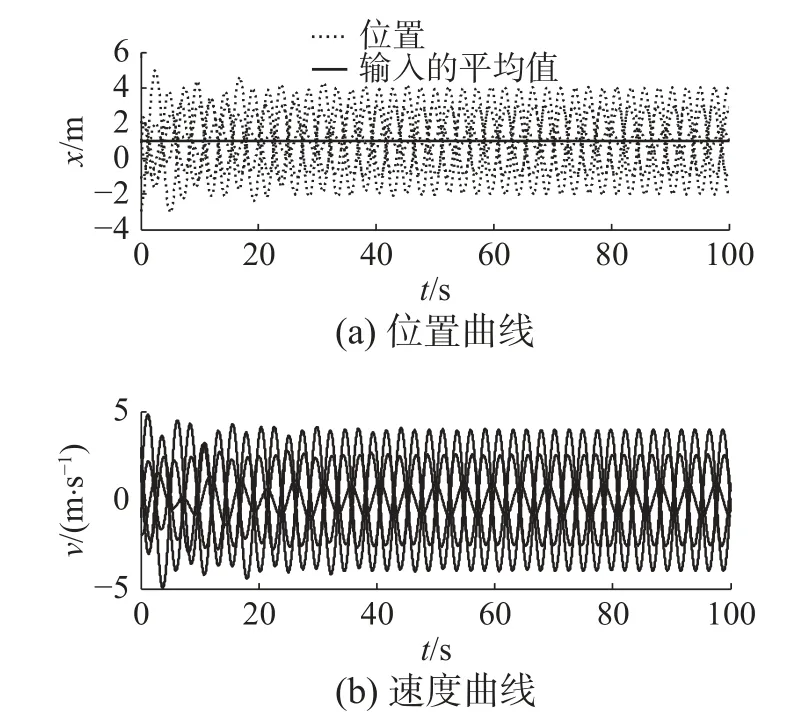
图3 智能体的位置和速度(k I= 0.483)Fig. 3 Positions and velocities of agents with k I= 0.483

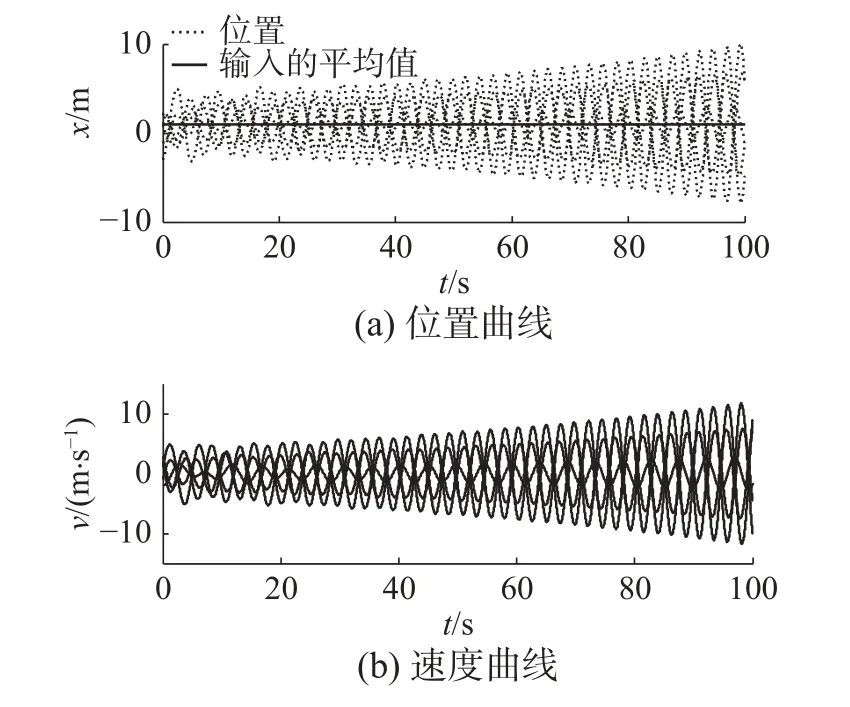
图4 智能体的位置和速度(k I= 0.5)Fig. 4 Positions and velocities of agents with k I= 0.5

3.2 时延二阶多智能体系统

针对具有通信时延的多智能体系统式(16)，选择和3.1小节中的相同连接拓扑、连接权重以及控制参数： k =1、 γ =0.3、 kp=0.4 、 kI=0.03。显然，定理2中的条件1)成立。根据式(20)和式(31)计算得：y2,3=0.311、 w2,3==0.5577、 T2,3=2.5414； y4,5=1.233、 w4,5==1.1105、 T4,5=0.7244。再根据定理2中的条件2)，系统式(16)渐近达到平均一致滤波的时延为 T ＜ 0.724 4 s。同时，在上述给定参数情况下，计算幅频特性的导数，得

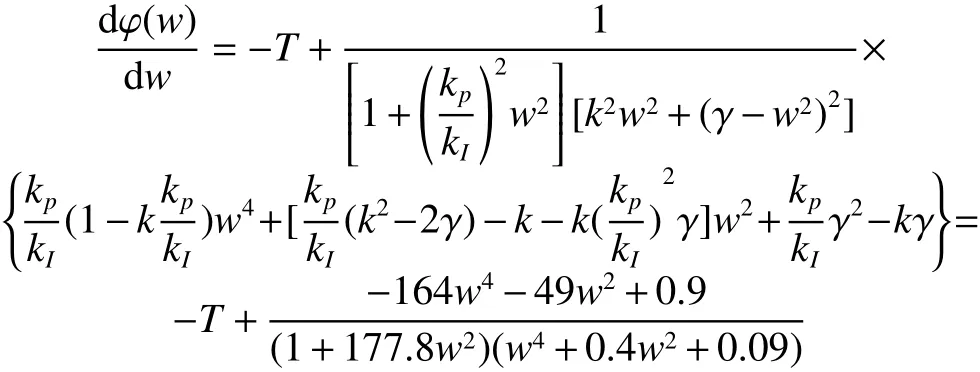
给定任意选择智能体的初始状态，且选择x(t)=x(0),t∈ [−T,0]；选择内部状态的初始值为η(0)=[2−1−3 2 0]T， 满足因此，当通信时延满足 T ＜0.724 4 s，智能体的位置轨迹渐近达到常量输入的平均值，且速度轨迹趋于零(如图5所示)。图6给定的通信时延是 T ＞0.724 4 s，各个智能体的状态逐步发散，不满足平均一致性。

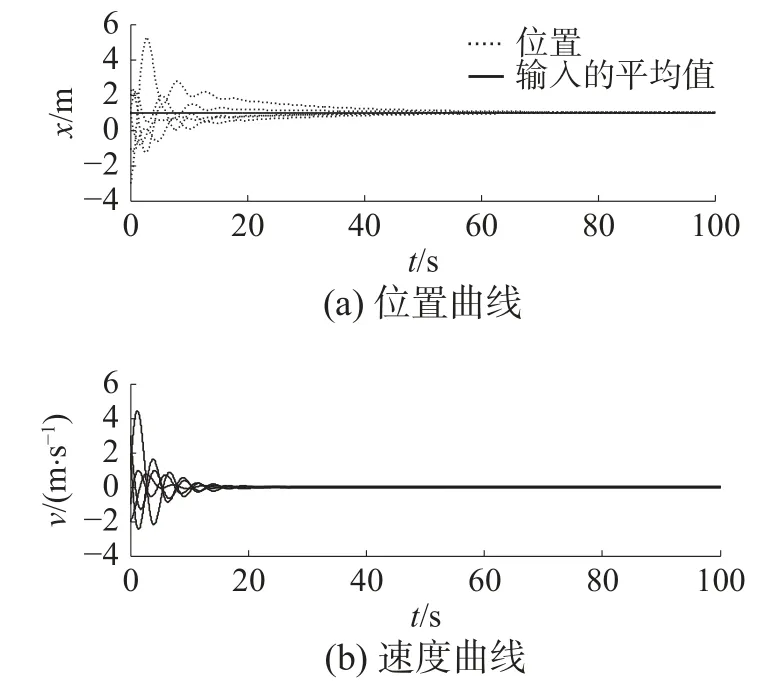
图5 智能体的位置和速度(T = 0.32 s)Fig. 5 Positions and velocities of agents with communication delay T = 0.32 s

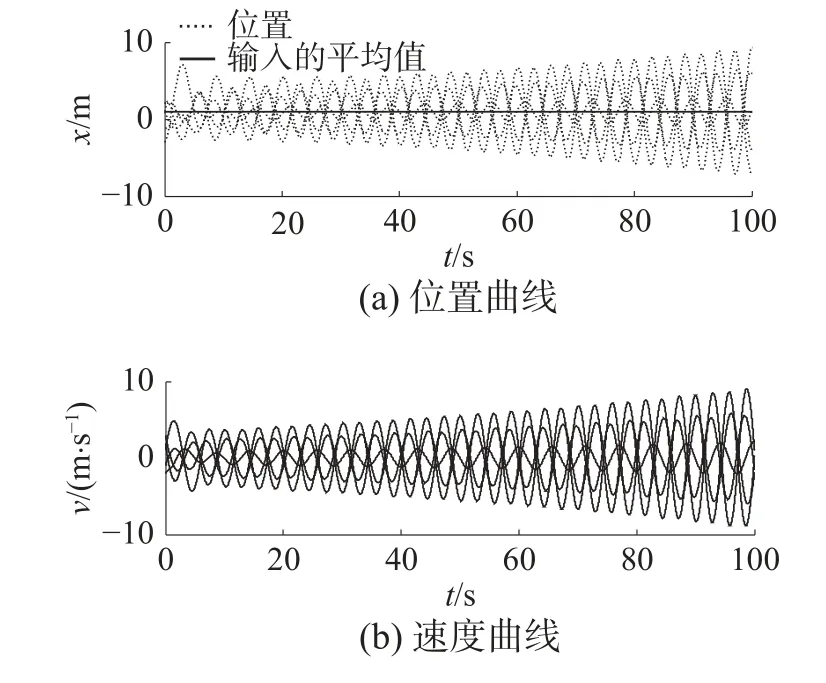
图6 智能体的位置和速度(T = 0.75 s)Fig. 6 Positions and velocities of agents with communication delay T = 0.75 s

4 结束语

针对具有定常输入的二阶多智能体系统的平均一致性滤波问题，本文研究对称连通拓扑结构下的一致性算法的设计与分析。本文设计一种PI型一致性滤波算法。利用Routh判据，分析二阶多智能体系统实现渐近平均一致滤波的充要条件。当系统存在通信时延的情况下，采用同步匹配的一致性算法形式，并利用Nyquist稳定判据得到二阶多智能体系统渐近收敛平均一致滤波的时延相关收敛条件，在特定参数条件下，该时延条件也是充要条件。