基于隐语义模型的智能推荐算法设计
鲁浪浪 袁庆达 凌源俊 林云鹏 王浩宇
摘 要 分析和研究如何根据用户偏好做到“智能推荐”。以向用户智能推荐图书为例,基于人工智能和机器学习的思想,利用隐语模型对用户进行大数据分析,实现对用户的精准化智能推荐。
关键词 智能推荐系统;隐语义模型;人工智能;机器学习
中图分类号 TP3 文献标识码 A 文章编号 1674-6708(2018)214-0124-03
在现代这个信息高速流通的时代,用户每天都会产生海量的数据,而根据大数据进行分析用户的偏好从而实现针对每个用户的精准化推荐也成为各个公司关注的焦点。而能够实现这个目的的算法已经成为公司的核心竞争力,如小红伞、今日头条、网易云音乐等App就凭借其出色的算法实现了精准营销在同类市场竞争中占据了优势。
自90年代以来,学界涌现了大量的推荐算法模型,代表性的如协同过滤算法。但由于数据量越来越庞大,协同过滤算法由于结构上的缺陷已经无法高效处理,基于此本文采用改进后的隐语义模型来实现高效准确的智能推荐。总的来说,根据大数据超高维、关系复杂等特点,需开展以下研究:
1)谋求大数据超高维、高稀疏知识发掘:钻研机器学习方法理论,构建特定数据挖掘算法。2)研究复杂算法编程,将挖掘算法编程模型与分布式处理相统一。3)在已有并行计算平台上,构建成分布式并行化机器学习、实现复杂度低、并行性高的发掘算法(何清、李宁、罗文娟、史忠植《大数据下的机器学习算法综述》)。
1 隐语义模型
隐语义模型LFM属于隐含语义分析技术,其本质在于通过数据分析找出潜在的主题或分类。文本挖掘领域首先采用该技术进行分析,近些年它们开始被应用到其他领域中,并取得了不错的效果。
隐语义模型的假设前提每个用户都有各自不同的偏好,以书籍为例,一个用户可能对历史类、战争类、科技类的书籍有特殊偏好,而这些偏好可以被抽象为一个个隐变量。每一本书在每一个隐变量上的权重综合构成了用户对这本书的偏好程度。
由此,产生了3个问题:第一,如何确定用户隐变量的个数;第二,如何求出每个用户在每个隐变量的偏好程度;第三,如何确定每本书在每个隐变量上的权重。
隐语义模型的核心内容是随机梯度下降(SGD),而这也是解决上述3个问题的关键。具体可分为以下步骤:
步骤一:矩阵分解
矩阵分解算法基于数学上的矩阵的行列变换。在线性代数中,矩阵A进行行变换相当于A左乘一个矩阵,矩阵A进行列变换等价于矩阵A右乘一个矩阵,因此矩阵A可以表示为A=PEQ=PQ(E是标 准阵)。
矩阵分解目标就是把用户对书籍的评分矩阵R分解成用户对隐变量评分矩阵和书籍在隐变量上权重矩阵的乘积。
首先假设,用户对书籍的真实评分和预测评分之间的差服从高斯分布,基于这一假设,可推导出目标函数。
最后得到矩阵分解的目标函数如下:
步骤二:随机梯度下降
从最终得到的目标函数可以直观地理解,预测的分值就是尽量逼近真实的已知评分值。有了目标函数之后,下面就开始介绍优化方法:随机梯度下降法(stochastic gradient descent)。
随机梯度下降算法是被广泛应用的一个算法,其主要思想是分别对用户-隐变量矩阵和书籍-隐变量矩阵求偏导,确定梯度下降方向,让变量沿着目标函数负梯度的方向移动,最终到达极小值点。求导公式如下:
梯度下降法具体分为以下几个步骤:
1)确定目标函数y=f(x);
2)对待优化的指标进行求导,确定每次迭代的搜索方向,见公式(2);
3)確定一个学习率α作为每次搜索寻优的 步长;
4)不断进行迭代优化;
5)满足迭代终止条件,最终使得待优化的指标迭代至目标值附近;
6)对通过上面的分析,可以获取梯度下降算法的因子矩阵更新公式,具体如下。
公式(3)中的γ指的是步长,也即是学习速率,它是一个需要调参确定的参数。对目标函数进行优化,学习率α的选择极其重要。若取值较大,即梯度下降迭代的步长较大,可以快速迭代至最优解附近,但是可能一直在最优解附近徘徊,无法计算出最优解,于特殊的函数也可能会导致不收敛,始终发散求不出解;若取值较小,即梯度下降迭代的步长较小,下降速度较慢,其迭代出的解精度较高,但会耗费很长时间,这将不利于实际 应用。
接下来的部分便主要介绍参数α和γ的调整过程。
2 推荐算法调参
2.1 实验方案与结果分析
智能推荐系统建立的关键是求解过程中参数的调节。本次实验的算法中主要运用到了随机梯度下降求解误差项达到了最优值的方法。该方法通过不断迭代使目标误差函数达到最小值。这次实验使用用户-电影训练集,测试集和验证集来检测算法效力。用户-电影测试集中有671个用户对9126部电影的打分,有10万条的数据。
实验主要是对隐语义模型的参数进行调节。需要调节的参数包括学习速率α、隐变量个数F、迭代次数N以及正则化参数。
2.2 调节的过程
步骤一:设置学习速率
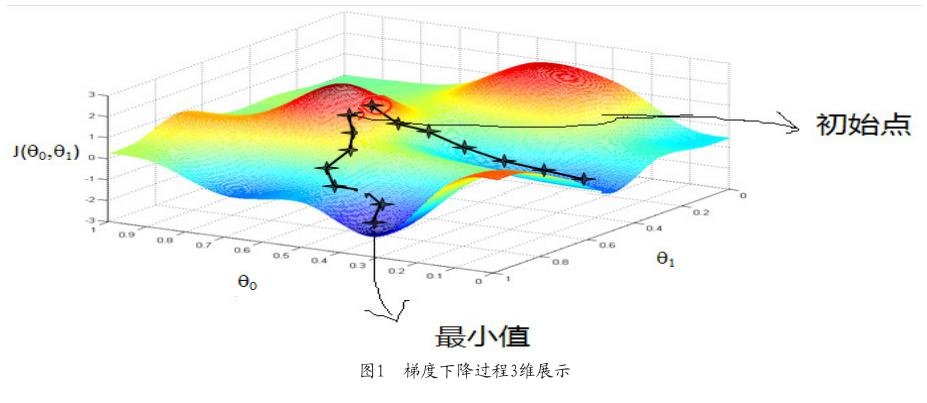
学习速率确定了学习速度的快慢。图1是梯度下降三维立体示意图。从图中可以看到迭代之前的初始点位于红色半坡位置,在运用SGD的基础上,算法会随机选择下一步迭代的方向,即图中的两条路线。学习速率可以用线路上两个十字星点的间距表示。
损失值可以用一条如图2所示的类二次函数的曲线来表示。当学习速率设置的过大时,就會导致从点1直接越过谷底即最优解跳跃到点2,如此循环往复,最终无法得到最优解,如图3η=2.5显示出的cost一样;当学习速率设置的过小时,就会在点1到点3的过程出现无数个间距无限小的点,在这种情况下,虽然能确保不会损失最优解,但迭代次数以及耗时也将会大大的增加,从而使得推荐算法耗时过长。
我们需要在迭代的不同阶段调整所使用的学习速率。前期迭代时运用一个大的学习速率能快速地择选出下降方向,在接近最优解时则使用一个小的学习速率使算法能精确得到最优解。所以,在算法中需要介入逐渐衰减的α,定义为每进行一次迭代就减少0.02,即乘上系数0.98。运用这种形式的学习速率的设置能更好地引导SGD快速而又有效地达到最优解。
步骤二:确定迭代次数
确定了学习速率的设置后,我们需要确定与之相关的参数,即迭代次数。迭代次数决定了学习速率发挥的程度,次数不够就会导致没有达到最优值便结束迭代,即欠拟合,反之次数过大就会造成时间上的巨大损失以及出现过拟合。前者可以使用网格搜索法,输入学习速率通过均值和标准差得出较好的迭代次数。后者除了可以用网格搜索法之外,还可以通过设置一个提前结束的条件,提前结束迭代。但仍需加上正则化系数使其避免出现过拟合的情况。在本次试验中,lamda即为用来避免过拟合的正则化系数。
步骤三:确定隐变量
最后一个待确定的变量为隐变量个数。隐变量的关键在于不用去定义元素,在运算过程中重要的是定义隐变量的数量,通过设置分类数就可以控制粒度,分类数越大则粒度越细。在实际运算过程中,设置过大的元素分类数会影响算法的准确性,基于学习速率,迭代次数和正则化系数调整好的情况,有时反而会适得其反地造成最终的得分的趋同。由于隐变量可查阅资料较少,根据实验中不断的测试优化,最后把隐变量确定在10。
综上,确定了各参数即学习速率为0.25,衰减速率为0.02,迭代次数为10000,lamda等于2以及隐变量为10,在这种情况下能较好地取到最 优解。
3 结论
智能推荐是根据用户的信息数据、爱好标签等,将用户感兴趣的信息、产品等推荐给用户的个性化信息推荐系统。和搜索引擎相比推荐系统通过研究用户的兴趣偏好,进行数据分析,发现用户的兴趣点,从而引导用户发现自己的需求。一个好的推荐系统不仅能为用户提供个性化的服务,还能让用户对推荐系统产生依赖,从而增进用户粘性。使用智能推荐还可以达到精准营销,节省企业大量时间和资源。在未来,一个高效准确的推荐系统必然会成为企业战胜对手的利器。
参考文献
[1]李学龙,龚海刚.大数据系统综述[J].中国科学:信息科学,2015,45(1):1-44.
[2]刘建国,周涛,汪秉宏.个性化推荐系统的研究进展[J].自然科学进展,2009,19(1):1-15.
[3]张亮.基于机器学习的信息过滤和信息检索的模型和算法研究[D].天津大学,2007.
[4]何清,李宁,罗文娟,等.大数据下的机器学习算法综述[J].模式识别与人工智能,2014,27(4):327-336.
[5]陈洁敏,汤庸,李建国,蔡奕彬.个性化推荐算法研究[J].华南师范大学学报(自然科学版),2014,46(5):8-15.
[6]刘红岩,陈剑,陈国青.数据挖掘中的数据分类算法综述[J].清华大学学报(自然科学版),2002(6):727-730.
[7]赵丹群.数据挖掘:原理、方法及其应用[J].现代图书情报技术,2000(6):41-44.

