模糊数学在茶叶感官审评中的应用
赵瑶
(湖北三峡职业技术学院 443000)
目前传统茶叶的感官审评多采用评分法[1],其评审指标有茶叶的外形、香气、滋味、汤色、叶底,评审方法通过对评审人员各项指标的权重进行加权平均,从而获得该茶叶的评定分数。采用评分法存在一些不足之处。首先,由于审评人员自身条件不同,所评定的分数往往离散程度较大,较难获得比较一致的结果,因此仅用一个平均数很难准确地表示某一指标应得的分数,存在的误差较大;其次,如果评定的样品超过两个,最后得出的加权平均数出现相同,而又需要排列出它们的名次时,现行的加权记分法就很难解决。如果采用模糊数学的方法来处理评定的结果,当两种样品属于同一等级,在进行排序时,可按照隶属度大小从大到小进行排序,由于它是综合考虑所有的因素,极大地消除了主观因素的影响,因而获得的是一个综合而比较客观的结果[2]。
1 数学模型的建立
以绿茶品质的感官审评为例,建立数学模型[2~3]。审评的品质指标为:外形、汤色、香气、滋味、叶底。评定级别为:一级、二级、三级、四级。由10名审评员进行感官评价。
首先根据模糊综合评判,设绿茶品质指标的论域为U:
U={外形( u1),香气(u2),汤色(u3),滋味( u4),叶底(u5)}
再设评语论域为V:
V= {一级( v1),二级( v2),三级( v3),四级(v4)}
评语可以用文字表示,也可以用具体数字或评定级别表示。这里用评定级别表示其中一级(91~100分),二级(81~90分),三级(71~80分),四级(61~70分)。
在审评时,由于各项指标对茶叶品质的影响程度不同,他们之间的关系不完全是平权的,因此需要考虑他们的权重,设权重因素为X:
X= {0.3( x1),0.2(x2),0.2(x3),0.2(x4),0.1(x5)},且x1+x2+x3+ x4+ x5=1
其中X的因素是U中的一个模糊子集(集合中的小集合),xn和un是相对应。审评时需要选定若干名有经验的审评委员对各项指标逐项评分。设审评委员人数为K,其中K= k1+k2+k3+···+k20。审评结果如表1:

表1 评委评判结果
将表1中所得数据分别除以评判总人数K,即得到一组关系,其中rij=ki/K,即为模糊矩阵T。

模糊矩阵T包含了与审评有关的所有模糊信息。茶叶感官指标综合评判的结果为Y,Y是模糊向量X与模糊矩阵T的合成。即Y=X⊕T,其中“⊕”代表两个模糊关系的合成运算。
2 合成运算方法
合成运算方法一般有如下三种[3~4]:
(1)模型Ⅰ M(∧,∨)——主因素决定型
Yj= max{ min (xi,rij),1≤i≤n }(j = 1,2,···,m)。
这种运算方法得到的综合评判的结果yj的值仅由xi与rij(i=1,2,···,n)中的某一个确定(先取小,后取大运算),着眼点是考虑主要因素,即由指标中最大项决定,其他指标在一定范围内变化也不影响评判结果。所以这种评判模型适合于单项最优就看作是综合最优的情形,而且这种运算有时出现决策结果不易分辨的情况。
(2)模型Ⅱ M(· ,∨)——主因素突出型
Yj= max{ (xi·rij),1≤i≤n} (j = 1,2,···,m)。
M(· ,∨)与模型M(∧,∨)较接近,区别在于用xi·rij代替了M(∧,∨)中的xi∧ rij,在模型M(· ,∨)中,对rij乘以小于1的权重xi表明,在考虑多因素时,xi是rij的修正值,与主要因素有关,忽略了次要因素。但M(· ,∨)模型的两个运算中的一个已较为精细,多少反映了些非主要因素的影响。
(3)模型Ⅲ M(· ,+)——加权平均模型
模型M(· ,+)对所有因素依权重大小均衡兼顾,适用于考虑各因素起作用的情况。在茶叶审评中需综合考虑外形、香气、汤色、滋味、叶底各因素,所以在茶叶审评时使用模糊综合评判时适宜选择加权平均模型。
3 模糊综合评判方法
目前采用方法有最大隶属度法、双权法,h 函数法、f 函数法,后两者是分别由前两种方法演变而成的方法[4]。
3.1 最大隶属度法
按照合成运算模型Ⅰ(主因素决定型),进行运算后,得到结果向量Yj,结果向量Yj中各分量代表的是产品感官质量处于各个评价分值或评语等级的隶属度,因此向量中最大的数值对应的等级即为该茶叶感官的等级。最大隶属度法对于消除少数评委的带有感情色彩的评判信息有一定的作用,但对结果向量中其他较小的分量却完全没有考虑,这同时丢失了一些不带感情色彩的符合客观实际的评判信息[5]。最大隶属度法的缺陷在于只能判定等级,不能对同一等级的产品进行准确地排序。而且当权重的分配较均匀时易出现双峰值,此时甚至无法判定等级。
3.2 双权法
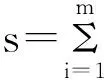
3.3 h 函数法
式中Yj也是按照合成运算模型Ⅰ计算得到的结果向量,突出了主因素,其中hj一般为与Yj相对应的n 个评语级别的等级系数,是人为定的数值,k一般取2。在评判结果向量中,较大的分量中包含了绝大多数的正确信息,较小的分量包含了较多的错误信息,所以为突出较大分量和压低较小分量的作用,以Yjk为权分别乘以各相应评语级别的等级系数,所得乘积求和后除以Yjk的总和。h 即为新的茶叶感官品质评价函数,根据求得的h 值接近哪个等级系数hj,即可判断该茶叶属于哪一等级,同时可按h 值排序。h 函数法解决了最大隶属度法不能排序的缺陷,但由于h 函数法计算中采用由最大隶属度法得出的Yj,因而在评判中突出了主因素,但忽略了其他因素,在实际应用中也会遇到无法排序或排序不尽合理的问题[4]。
3.4 f 函数法
其中k=2,在形式上 f 函数法与h 函数法相似,其中hj一样为与Yj相对应的人为定的数值,区别是其中的Yj是按照模型Ⅲ计算得到。当k = 1时,f 函数法与双权法等同。在某些特殊的情况下,结果向量会出现分散的现象。即出现双峰值和多峰值[6],有一定的原因,如果茶叶的感官质量指标u1,u2,u3···un不均衡,这一指标高,而另一指标又低,评判结果就有可能出现分散,这是客观存在的;另外评委意见有一定的分歧也会造成分散,这就包含了一定的感情色彩,不符合客观实际。双峰值和多峰值问题可以通过更换合成运算方法进行改变,一般采用双权法或f 函数法进行处理可以得到单峰值。
4 两种绿茶感官品质的模糊综合评判
4.1 设绿茶品质评定论域U
U={外形( u1),香气(u2),汤色(u3),滋味( u4),叶底(u5)}
4.2 设评语论域V
V= {一级( v1),二级( v2),三级( v3),四级(v4)},其中一级91~100分,二级81~90分,三级71~80分,四级61~70分。
4.3 建立评判矩阵
假定绿茶的感官审评由10 人组成,用打分的方式表明各自的评判,评判结果见表2、表3。

表2 1号绿茶感官评判结果

表3 2号绿茶感官评判结果
从表2、表3得到模糊关系矩阵分别为:


4.4 综合评判
用强制确定法确定外形、香气、汤色、滋味、叶底各自的权重X:
X= {0.3( x1),0.2(x2),0.2(x3),0.2(x4),0.1(x5)},且x1+x2+x3+ x4+ x5=1。
(1)最大隶属度法评判结果
根据合成运算模型Ⅰ(主因素决定型),进行运算后,分别得到1号绿茶和2号绿茶的结果向量Y为:
1号绿茶:Y1=(0.2,0.3,0.3,0.2 )
2号绿茶:Y2=(0.2,0.2,0.3,0.1)
从结果向量看,出现了双峰值,y1= 0.3,y2= 0.3,无法判定1号绿茶的等级。而2号绿茶的等级可根据最大隶属度原则判定为三级茶,但一级和二级的Y 值是一样的,都为0.2。可以看出最大隶属度法不能保证结果的惟一性,对茶样无法做出评判。
(2)双权法评判结果
依据合成运算模型Ⅲ运算后,分别得到两样品的结果向量Y:
1号绿茶:Y1=(0.09,0.55,0.29,0.07)
2号绿茶:Y2=(0.14,0.47,0.33,0.06)
将结果向量与 H = (100,90,80,70)相乘,则:
1号绿茶: s1= 86.6
2号绿茶: s2= 86.9
用双权法评价的结果表明,1号绿茶和2号绿茶都为二级,而且2 号绿茶要优于1 号绿茶。最大隶属度法比较,用双权法得出的Yj没有忽略任何影响因素, 更为客观,既评出了茶样的等级,又可以给同一级别的茶样排序。
(3)h 函数法评价结果
用合成运算模型Ⅰ计算得出的结果向量Y(即最大隶属度法得出的结果)代入h 函数法中的h 计算式得到{其中H = (100,90,80,70)}:
1号绿茶:h1= 85.0
2号绿茶:h2= 86.1
从结果可以看出,两个样品的感官质量等级均为二级,2号绿茶要优于1号绿茶。因此,从这个意义上看,h 函数法是在最大隶属度法的基础上作了改进,实现了对多个样品的排序。
(4)f 函数法评价结果
依据合成运算模型Ⅲ运算后得到的结果向量Y,代入计算公式,其中H = (100,90,80,70),得到:
1号绿茶:h1= 86.9
2号绿茶:h2= 87.3
可见,用f 函数法评价两个样品,与上述各法得出相同结论。用f 函数法亦实现了对差距不大的多个样品进行排序,对处于同一等级的不同样品的优劣也可以作出判断。
5 结论
从上述的分析中可以看出,最大隶属度法不能判定1号茶的等级,不能保证结果的惟一性,在茶叶感官审评时采用最大隶属度法具有局限性。双权法、h 函数法、f 函数法得出两个绿茶样品均为二级,且对于同一等级的茶叶亦能通过得分分出优劣,实现对多个样品的排序。h 函数法,仍然是采取最大隶属度法得出的Yj,突出主因素,具有局限性。f 函数法与双权法相比放大了样品之间的差距,更有效地对品质相近的茶叶进行排序。
茶叶这种食品因其自身复杂多样的特点,在评定其品质时需要更加客观、综合的方法。现阶段茶叶品质评定方法的主要特点[8]是在测定茶叶物理、化学因素数据的基础上,运用非线性数据处理方法来寻求茶叶品质与品质因子之间错综复杂的非线性对应关系,以建立相应的茶叶品质评定模型。模糊综合评判也是非线性数据处理中的一种方法。
自20世纪80年代吕志俭[2]将模糊数学综合评判法引入食品感官质量的审评以来,食品界出现模糊综合评判热,有很多应用及方法讨论的文章发表,朱余尧[9]发表了应用模糊综合评判进行食品感官质量的实施报告,兰景波[7]等发表了关于模糊数学综合评判食品感官质量方法的讨论;晏孝皋[10~12],闫喜霜、何卫东[13]还介绍了模糊数学法与计算机联用在食品审评与检验中的应用。而专门针对模糊数学在茶叶品质评定中应用的报道不多。模糊数学综合考虑评判人员的意见,采用比较科学的处理方法,得到的结果不仅使评定结果的客观性增加,还能进一步区别多种茶叶感官品质之间的差别,使评定的结果更客观和更准确,而且计算机又能为其应用提供方便的工具。从这些方面看来模糊数学在茶叶品质研究中的应用有着广阔的前景。

