波 动 率 与 公 司 预 期 寿 命
——基于ZZ破产成本模型的研究
张志强
(中国人民大学 商学院,北京 100872)
关于公司预期寿命的研究结论对于许多决策都有重要意义,比如,未来商业合作的考虑(潜在合作伙伴的决策)、未来投资的考虑(潜在投资者的决策)、未来贷款的考虑(相关银行的决策)以及公司管理者和员工的个人职业发展决策等。值得提醒的是,决策总是面向未来的。公司寿命的研究如果要有决策意义,就不能停留在事后的统计和描述上,必须进一步发展到对公司预期寿命的事先研究。也许,与事后的统计相比,事先的估计要难得多;但科学研究的目的和意义就在于攻克难题,不应该知难而退。
一、经典案例回顾
2011年,美国第二大书店Borders结束了其40年辉煌的历史,申请破产。2016年,我国钢铁行业的标杆公司——武钢股份因严重亏损不得不依靠宝钢股份吸收合并来延续经营。也许从全球角度看,这两家公司不是非常有名。但可以想象,在Borders破产前后不知有多少书店遭遇破产命运;在武钢舍身前后不知有多少钢铁公司难以为继。即便再著名的公司,也难逃破产消亡的结局。
1850年创立的雷曼兄弟公司(Lehman Brothers),凭借一百多年的努力,成长为全球性多元化的投资银行,被公认为全球最具实力的股票和债券承销商之一,在最佳投资银行以及最强调研实力等排名中常常位列前茅,公司总资产一度高达6 390亿美元。然而,2008年9月15日,负债6 130亿美元的雷曼兄弟公司成为次贷危机中的先烈。1881年成立的柯达公司(Eastman Kodak),作为胶卷、胶片和大众用相机以及数码相机的发明者,在全球市场长期保持领先和最大,一度占据全球2/3的胶卷市场。然而,随着摄影进入“数字时代”,柯达公司业务持续萎缩、利润锐减,不得不在2012年1月申请破产保护,走上不归之路。1865年成立的诺基亚公司,开始以造纸为主业,后于1960年开始手机生产。从1996年开始,连续15年稳据全球手机市场份额第一,巅峰时期拥有超过38.6%的市场份额。然而,随着iPhone与安卓系统的崛起,诺基亚丢寨弃城,一路溃败;最后于2013年将手机业务卖给了微软,要价54.4亿欧元,不及诺基亚辉煌时1年的净利润[1]。1994年创立的雅虎,崛起于互联网时代,是早期互联网的绝对霸主。随着门户网站业务的衰退,谷歌、Facebook、亚马逊等后来居上,以搜索引擎、社交及电商等精准定位崛起于互联网江湖。雅虎累计耗资170亿美元大肆收购,但却错失了收购谷歌和Facebook的机会,大量的低效并购反而成为其发展的拖累。2016年7月,包括搜索引擎在内的雅虎核心资产以48.3亿美元的价格卖给了美国电信巨头Verizon[1]。
当然,在人类历史上,倒下的“龙头”、“羊头”公司又何止这三五家,也不止三五十家甚至三五百家。从某种意义上讲,在众多倒下的公司中,这些公司堪称英豪,也堪称幸运。因为许多公司并未经历奋斗、成功、辉煌然后衰败的完整过程,只经历风雨并未见彩虹就破产倒闭了。据统计,人类发展至今,寿命最长的公司也不过1 000年出头;而真正历经1 000年还屹立不倒的公司寥寥无几,在全球也不超过10家。
也许有人知道,上述大牛公司有的并非完全销声匿迹。比如诺基亚,失去手机业务后,将主业调整为运营商业务,并在2015年宣布与阿尔卡特-朗讯达成合并协议,要打造引领下一代互联世界的创新公司。柯达公司还在2016年6月宣布,要与阿里巴巴共同投资开发新型隐形墨水。柯达公司也宣布要集中精力发展微型3D打印机业务。然而,可以想象,无论公司在市场的风浪中如何转型,都难逃覆灭的命运;无论被并购(解救)多少次,也难逃最终随并购主体公司一起消亡的结局。
那么,公司寿命预期会有多长呢?抛开迷信、玄学等不论,现实中的预测大致包括统计和周易两大方法体系。由于这两大方法影响极其广泛,其他学科在公司寿命预计中的作用几乎被埋没或忽略了。本文运用概率论(而非统计回归)和金融专业方法探讨公司寿命的预测,希望可以为商业银行、担保公司、保险公司以及各类工商业公司和金融机构的风险管理和相关决策带来有益的启示。
不难想象,公司的寿命与其所冒的风险相关。在金融领域,所谓风险通常指不确定性,主要指收益的不确定性,常用投资收益率的标准差(σ)来计量,也称为波动率。从长期来看,公司资产收益的波动不能突破一个底线,这就是债务还本付息的需要。突破了这个底线,公司就资不抵债,就将破产倒闭,导致寿命的终结。
由此可知,公司寿命与其整体风险和负债率有关;当公司破产概率足够高时,公司就将破产倒闭。因此,要推算公司寿命,就需要知道上述两方面影响因素与公司破产概率之间的定量关系。基于有关理论和知识,目前有两种方法可以计算这个破产概率,从而也就有两种方法可以推算公司预期寿命:一种是基于经验数据进行推算,另一种是依据理论模型进行推算。
二、基于穆迪公司的违约概率计算公司预期寿命
作为世界最大的风险评级公司,穆迪公司记录并积累了大量公司从生到死的寿命周期过程。穆迪公司基于1970—2010年期间积累的数据计算的各风险级别公司累积违约概率[2],虽然概念上略有差异,但可以大致将穆迪的违约概率看做破产概率。
注意穆迪公司给出的是累积破产概率,也就是在若干年中破产一次的概率。根据排队论原理,如果有年均破产概率,其倒数便是公司预期寿命。因此,为求公司预期寿命,下面先着重探讨如何计算合理或有效的年均破产概率。有了累积破产概率,也就不难得出年均破产概率,用P和p分别表示一家公司在n年中的累积破产概率和年均破产概率。则有[3]:
P = 1- (1-p)n
(1)
这意味着:
p = 1- (1-P)1/n
(2)
因此,根据累积违约概率[2],可以计算得到各风险级别公司的年均破产概率,如表1所示。

表1年均破产概率:基于1970—2010年数据 单位:%
资料来源:根据穆迪公司数据计算,下同。
可以理解,根据1—20年期的累积破产概率的每一个都可以计算出一个年均破产概率,而这些年均破产概率又各不相等,这就是表1中的数据。究竟哪一个更能代表相应风险级别的年均破产概率呢?这个问题难以做出有依据的回答。因此,表1在最后一列计算了这些年均破产概率的平均值。可以认为,这个平均值更有代表性。
然而就公司未来长期而言,这个平均值的代表性并不足够。即便不追究更多细节问题,公司未来的一个变化不能忽略——在长期中,公司的风险级别会发生变化。也就是说,在足够长的时间中,一家公司可能会从目前的风险级别变化到任何其他六个级别,从而年均破产概率就会不同。虽然年均破产概率也许差异不大,但微小的差异经年累月地积累,其效果就不可忽略了。因此,对于目前处于特定风险级别的任何一家公司而言,表1的年均破产概率平均值并不是长期适用的年均破产概率。
要得到长期适用的年均破产概率,还需要在表1年均破产概率平均值的基础上,再考虑风险级别的变化。也就是考虑在未来长期中,一个级别的公司将以什么概率升或降到其他级别[3]。具体公司具体时间在各个风险级别之间变化的概率需要结合具体情况进行探讨,这里不做进一步分析。为集中探讨估计公司预期寿命的一般思路和方法,简单(而不失合理地)假定长期平均来看,公司每年变动到临近第1个、第2个、第3个、第4个、第5个、第6个级别的概率分别是6%、5%、4%、3%、2%、1%;从100%中扣除变动到各个级别的总概率,就得到保留在目前级别的概率。
例如,目前处于Aaa级别的公司,变动到Aa级别的概率为6%,变动到A级别的概率为5%,变动到Baa级别的概率为4%,变动到Ba级别的概率为3%,变动到B级别的概率为2%,变动到Caa级别的概率为1%;这些概率之和为21%。因此,保留在目前级别的概率为79%。目前处于Aa级别的公司,变动到Aaa和A级别的概率各为6%,变动到Baa级别的概率为5%,变动到Ba级别的概率为4%,变动到B级别的概率为3%,变动到Caa级别的概率为2%;这些概率之和为26%。因此,保留在目前级别的概率为74%。以此类推,可以得到如表2所示的长期适用的年均破产概率。取表2中长期适用年均破产概率的倒数,就得到公司的预期寿命,如表3所示。
根据表3,目前A级以上的公司有望达到百年以上的寿命,其中Aaa级的公司有望达到200年以上的寿命;B级到Baa级的公司有望达到10—100年之间的寿命;而Caa级以下的公司寿命平均为9年;可以想象,这个级别许多公司寿命都在10年左右。
短到10年左右,长到200年左右,现实中公司寿命的确基本如此,这也反映出上述分析在两方面的正确性或可靠性。一方面是穆迪公司的数据量足够大,基本可以反映现实公司的总体情况;另一方面是上述对穆迪数据的基本分析和计算方法是正确或合理的。也就是说,从违约概率到公司寿命的推算方法是正确或合理的。
不难明白,上述测算过程虽然是针对所有风险级别公司得出各级别公司的寿命分布,其实也适用于测算一家公司的寿命。就一家公司而言,先要搞清楚该公司的风险级别以及若干年中的累计违约概率。有了这样的基础数据,就可以运用文中的方法计算年均破产概率以及长期适用的年均破产概率,进而计算出公司的寿命。
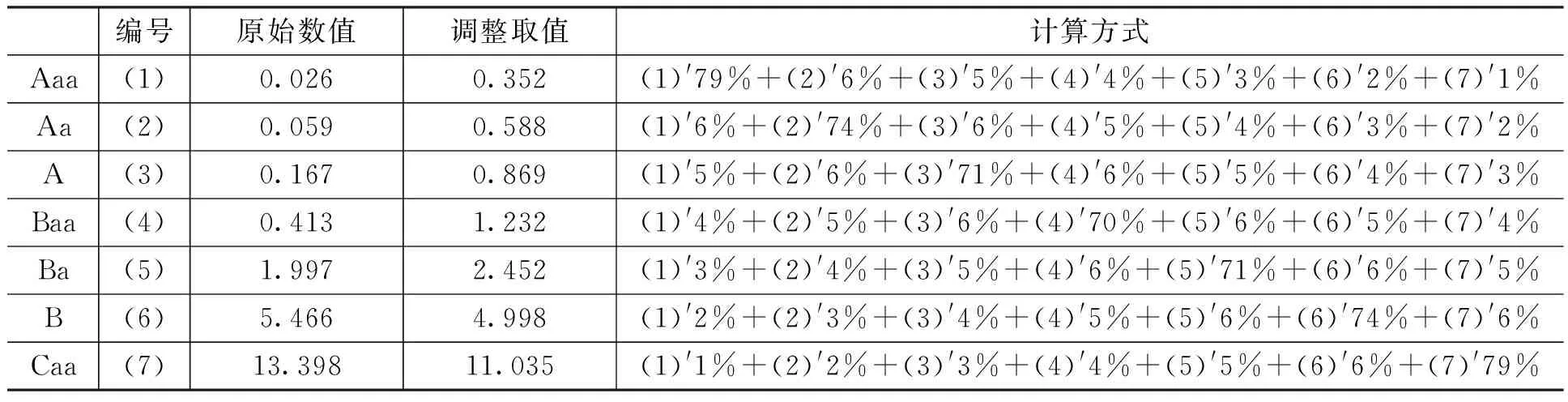
表2年均破产概率:长期适用取值

表3各风险级别公司预期寿命(年)
三、基于破产成本模型计算公司预期寿命
为解决公司最优资本结构问题,张志强和赵全海与张志强和肖淑芳[4-5]纠正了针对破产成本的长期误解,进而分析得出,公司与负债相联系的破产成本实际是该公司价值的卖方期权。这个卖方期权的约定价格为所有债务的到期价值(本息和);到期时间为所有债务的平均到期时间。在此基础上推导建立了ZZ破产成本模型,即:
BC = XN(-d2) -SN(-d1)
(3)
其中,BC 为破产成本;S为公司目前价值;X为公司债务的本金,按照研究惯例,它也是债务的现值。注意X/S = L,代表了公司的债务比率或负债率。N(-d2)和N(-d1)分别为标准正态分布中变量值取-d2和-d1时的累积概率。其中,d1和d2可分别按式(4)、式(5)求得:
(4)
(5)
其中,T为公司债务(平均)年限或考察期限;σ为公司总体资产的波动率。根据期权定价原理,N(-d2)为该(卖方)期权到期执行的概率,此处也就代表公司在整个债务期间的破产概率,即累积破产概率。从而有:
(6)
式(6)是基于ZZ破产成本模型得到的破产概率模型,可称为ZZ破产概率模型。根据ZZ破产概率模型,公司破产概率取决于公司整体风险(σ)、公司负债率(L)以及考察周期(T)三大变量。注意,ZZ破产概率模型不是简单的线性或非线性回归模型,也不是人为选择的二次或三次或指数或对数模型;无论是模型的形式还是模型中的变量,都不是主观选择或确定的,而是破产概率与其影响变量之间客观定量关系的表达。
前面经过分析认识到,要预测公司寿命,就要搞清楚公司破产概率与其整体风险和负债率之间的定量关系。比如,模型中有几个自变量,这些自变量各是什么,这些自变量与因变量(破产概率)之间是什么关系等。这些问题的回答如果都是主观猜想或假设的,模型的正确性和有效性恐怕就值得怀疑了。现在,在ZZ破产成本模型的基础上,ZZ破产概率模型轻而易举地揭示出这其中确切的定量关系,可见本文选择了有效且高效的研究方法。
要应用ZZ破产概率模型,就需要先确定公司波动率(σ)、负债率(L)和考察周期(T)三大变量的值。可以理解,考察周期(T)取决于研究的目的,不难确定。在研究对象(一家或一组公司)确定的情况下,公司或公司总体平均的负债率(L)也不难确定。这样,较为难以确定的变量就是波动率(σ)了。其实,这个波动率(σ)也不难确定。在公司为上市公司的情况下,通常可以利用股票交易数据计算这个波动率。用St和St-1分别表示公司在第t期(天)和第t-1期(天)的股票价格。令 Ut= ln(St/St-1),以s估计u 的标准差,则有:
(7)
其中,n为期数;s为相应期收益率的标准差。如果每期的长度不等于年,则需要将估计出的s进行年化换算,之后就得到波动率σ。
即便没有股票交易数据,这个波动率也不难确定,因为有大致的经验值范围可以借鉴。首先应该明确一下概念,这个波动率代表的是公司总体的风险,即是公司总资产收益率的标准差。由于公司总资产由股权和债务价值组成,为简单起见,假定公司股权和债务之间不相关,则公司总资产(简称公司,下同)的波动率为公司股票(或股权,下同)和债务(或债券,下同)波动率的加权平均数。
根据美国股市的长期经验数据,传统行业股票的波动率主要分布在20%—40%的范围。我国股市公司之间波动率差异或跨度会更大一些,比如多数股票在10%—50%之间。可以想象,特别好的公司,比如类似于Aaa级的公司,这个波动率可能接近10%;特别差的公司,比如类似于C级以下的公司,可能接近60%。近年来随着高科技公司、互联网公司以及各种创业公司的大量涌现,这个波动率范围上限有所上升,粗略估计大约在70%左右。(数据主要来源于万德数据库)
公司整体的风险或波动率基本反映在股票的波动上。因此,根据股票的波动情况可以大致估算公司的波动率。下面基于上述多数股票波动率范围对公司总体波动率做简单估计;然后就可借助ZZ破产概率模型推算公司的破产概率进而寿命分布,这是本文的重点。希望由此可以得到借助ZZ破产概率模型推算公司寿命的有效方法。
根据上面的分析,多数股票波动率范围为10%—70%;公司债务波动率显著低于股票,粗略按股票波动率的1/5计算,则范围在2.0%—14.0%之间。假定公司资产负债率为50%,且债务和股权之间不相关,则公司波动率为公司股票和债务波动率的加权平均数,其下限在6.0%(=2.0%/2+10%/2)附近;其上限在42.0%(=14.0%/2+70%/2)附近。*不同市场、不同时期的股票波动率会有差异。精确估计具体单只股票的波动率或市场总体的波动率范围是一个值得探讨的问题,但不是本文的主题和重点。因此,这里只做简单粗略的估计,目的是为了后面探讨公司预期寿命的测算方法提供一个大致合理的基础数据。
分别以6.0%和42.0%作为公司波动率取值最低和最高组的组中值,将这个范围分成7个等距离区间,即3.0%—9.0%、9.0%—15.0%、15.0%—21.0%、21.0%—27.0%、27.0%—33.0%、33.0%—39.0%、39.0%—45.0%;分别用A、B、C、D、E、F、G命名这些风险组,对应的组中值分别为6.0%、12.0%、18.0%、24.0%、30.0%、36.0%、42.0%。假设公司债务比率为50%,在债务期限为1—20年情况下,根据ZZ破产概率模型即式(6)分别计算各个风险组的累积破产概率,如表4所示。

表4各风险组的累积破产概率 单位:%
资料来源:基于ZZ破产成本模型计算。
在表4的基础上,计算各风险组的年均破产概率,如表5所示。同样,这个年均破产概率并不是长期适用的年破产概率。考虑风险级别的变化,按照表2的思路和计算方式调整,制成表6。在表6长期适用年均破产概率的基础上,计算各风险组公司的预期寿命,如表7所示。

表5各风险组的年均破产概率 单位:%

表6长期适用年均破产概率 单位:%

表7各风险级别公司预期寿命(年)
比较表3和表7的预期寿命结果可知,按照同样的计算步骤,基于穆迪违约概率数据和基于ZZ破产概率模型计算的结果较为接近。注意本部分计算中虽然也按照风险将公司分为7个组别,但只是按照波动率σ取值等距离分组,与穆迪的分组其实很可能有所差异,比如各组在总体中的比重等。在分类有差异的情况下得到这样相近而且大致符合实际的结果,可见本文两种专业方法具备初步的合理性和可靠性。
严格讲,ZZ破产概率模型计算出来的破产概率与穆迪违约概率数据可能略有不同。ZZ破产概率模型相当于假定公司保持目前的波动性,即保持风险管理力度和有关外部条件不变直到破产发生。而在现实中,公司在出现违约或破产危险时,会采取各种自救或求助措施,即加大风险管理力度,因而会改变波动性。对于曾经的Aaa等高级别公司而言,这种努力可能会格外有效,从而使公司避过险关。相反,对于风险级别较低的公司而言,可能会有外部的过激反应,稍有风吹草动就迅速恶化,加大风险管理力度也无济于事。穆迪违约概率作为统计数据,自然将这种人为努力和外部反应的效果包含在内。因此,测算出的Aaa和Aa等高级别公司的寿命可能会更长;而Caa等低级别公司的寿命则会更短。
这进一步解释了基于ZZ破产概率模型与基于穆迪违约概率数据的计算结果差异。也就是说,如果考虑不同风险级别公司出现破产危险时波动率的变化,两种计算方法的结果会更为接近。无论如何,大致也可以说,基于ZZ破产概率模型的计算显示,各风险级别公司总体的寿命短到10年左右,长到200年左右,与现实中公司实际情况基本相符,与穆迪公司的数据结果也基本相符。读者至此也可以明白,本文选择测算公司总体的寿命分布范围而不是测算单一公司寿命的用意,即这样可以直接检验所用方法的正确性和有效性。
当然同样,上述测算过程虽然是针对所有公司得出各风险级别公司的寿命分布,其实也适用于测算任何一家公司的寿命。就一家公司而言,先要估算该公司的波动率(σ)、负债率(L)和考察周期(T)三大变量的值,然后就可以运用ZZ破产概率模型计算年均破产概率以及长期适用的年均破产概率,进而计算出公司预期寿命。
四、总结与启示
上述研究表明,公司寿命与公司年破产概率相关,而年破产概率又取决于公司目前风险状况或风险级别。考虑到公司未来风险状况或风险级别的变化,可以得出长久适用的年破产概率。这个长久适用的年破产概率可以基于穆迪长期积累的数据计算得出,也可以基于ZZ破产成本或ZZ破产概率模型计算得出,在此基础上就很容易计算公司预期寿命。不仅如此,ZZ破产概率模型还清晰地揭示出公司寿命与相关因素之间的确切定量关系。
应用概率论方法和金融专业方法计算公司预期寿命,在目前还是创新性的尝试。本文经过初步探讨,得出较为切合实际的结论;特别理想的是,两种方法计算结果较为吻合,计算出的各风险级别公司总体的寿命大致都在10年左右到200年左右。这意味着这两种计算方法都有合理性和可信性,有进一步深入研究的价值和应用潜力。另外,作为本文理论基础的ZZ破产成本模型,属于财务和金融的基础理论突破,除了张志强和肖淑芳[4]借此推出最优资本结构模型,其他的运用还不多见,本文从中推出ZZ破产概率模型,并应用到公司寿命的推算,算是另一个粗浅尝试。
可以理解,关于公司预期寿命的研究在公司前景展望、收益预测、价值评估、风险评级以及风险管理等诸多方面都值得考虑和应用。以公司或其股票价值评估为例,在常规的评估中,收益折现方法是理论上最为合理的方法。所谓收益折现即指将未来所有收益折算为当前价值,然后加总这些折现值得到相应资产的价值。理论上讲,应该折现和加总公司未来所有年份的收益,但逐年预测这些收益过于困难且无助于提高评估的准确性。一般做法是估计一个有代表性的初始收益并预测一个年均增长率,就可以表达出未来所有的收益。显然,无论是未来年份总数还是这个年均增长率,都可以根据公司寿命推算[3]。
要正确地测算实际公司的预期寿命,一方面是选择正确的理论和方法;另一方面是正确估计基础数据。本文重点是探讨公司预期寿命测算的方法,因而强调理论上的合理性与逻辑上的严谨性。测算过程中有关基础数据的估算有一定合理性,但最好不要照搬。原因在于基础数据虽然同样重要,但不是本文主题,文中多数情况下都寻求简便方法以求少用文字和篇幅,所以可能不是最佳方法,更未必能达到精确度的要求。基础数据究竟如何估算更为合理有效,需要留待另外的研究来解决。

