新形势下高中数学教学与多媒体技术的融合分析

苏灿强

（福建省安溪第一中学 福建 安溪 362400）

多媒体技术应用直接改变传统教学模式，高中数学中多媒体技术作为重要教学工具，通过应用多媒体技术，有效优化教学过程与教学质量，完成数学教学目标，本文就此展开论述。

一、高中数学教学与多媒体技术融合原则

1.技术辅助原则

多媒体技术在人们工作生活中普遍应用，高中数学教学中融入多媒体可以推动教育改革。具体教学时教师要避免过度重视多媒体技术而忽视其他。高中数学教师充分利用多媒体技术优势，扬长避短，活跃课堂氛围。

2.质量第一原则

高中数学多媒体技术应用应该充分考虑各方面因素，控制信息量，避免信息量过大让学生产生畏惧心理，进而学习陷入到困境中。因此高中数学充分考虑学生实际情况，坚持质量第一的基本原则。

3.双向沟通原则

教学过程应该是教育与学习融合的过程，整个过程中教师与学生之间加强沟通，确保双方对数学认知的一致性。合理利用多媒体技术，提升师生间关系，促使学生更好吸收数学知识。

二、高中数学教学与多媒体技术融合方法

1.概念教学中融入多媒体技术

数学概念就是反映客观事物中数与形的本质属性，一般情况下人们通过感觉、知觉认识客观事物。利用几何画板开展教学可以提高教学质量，突破概念教学难点。

如，椭圆概念与知识点教学。

实验工具：“几何画板”为基础的实验平台

实验过程：（学生为主、教师为辅，学生自己动手、全面探究）

保证每个学生一台电脑，利用几何画板中的点、线段、圆等工具按键和点的追踪功能掌握椭圆的概念。

步骤1：根据椭圆定义，取线段AB长为定值，在线段AB上随意取一点定为E,线段AE、BE长度分别为F1和F2，分别以F1和F2为半径画圆，圆心也为F1和F2，两圆的交点轨迹符则合题目要求。

步骤2：根据现有条件让学生各抒己见，大胆猜想，如果移动圆心，两圆相交的轨迹将组成一个什么图形。

步骤3：让学生动手拖动两圆圆心，并对两圆交点进行追踪记录，得出如图2-1所示的交点轨迹，给学生眼前一亮的感觉——椭圆。

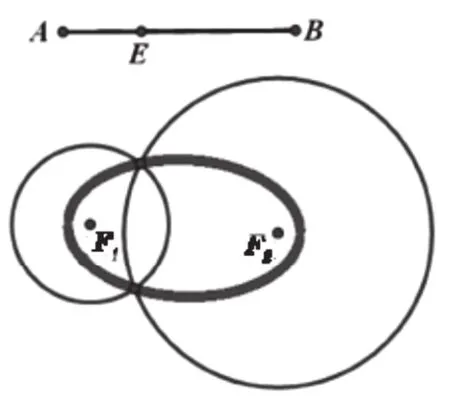
图2-1 两圆交点运行轨迹

步骤4：跟学生一起，根据刚才移动经验总结椭圆概念。

步骤5：再次推动两圆圆心，改变线段AB的长度，使得|AB|=|F1F2|和|AB|＜|F1F2|，如图2-2所示，观察这两个图形中圆的交点关系，引导学生积极思考，为下一步椭圆焦距与长轴大小关系学习做好铺垫。

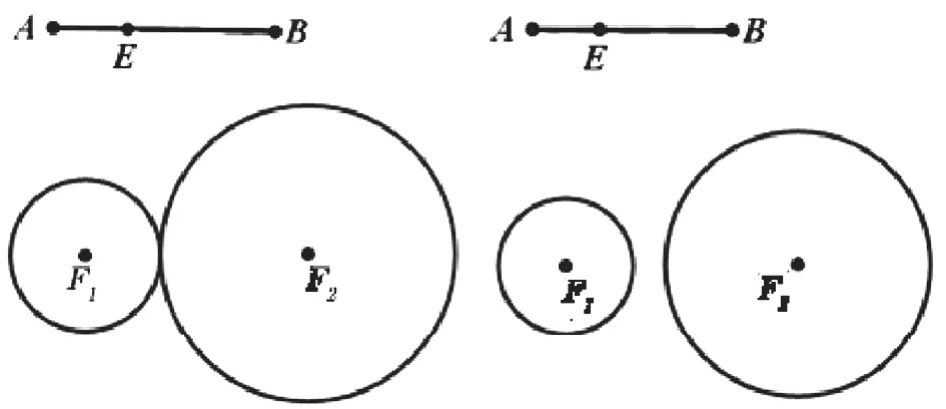
图2-2 |AB|=|F1F2|圆的交点关系（左）与|AB|＜|F1F2|的圆的交点关系（右）

2.抛物线与标准方程教学中几何画板应用

为了详细讲解几何画板的应用，本部分直接联系问题开展分析。

例 一个平面内，动点M满足到定点F与到定制线L的距离比为常数e（e＞0）。若0＜e＜1则动点M的运行轨迹为椭圆；若e＞1则动点M的运行轨迹为双曲线。请问：当e＝1时，求动点M的运行轨迹。

引入几何画板则可以解决上述问题。

第一步，将直线L与定点F画出，注意定点F并不在直线L上；

第二步，直线L上随意取一点P，过点P做直线L的垂线L1；

第三步，连接点P与点F，做出线段PF的中垂线L2；

第四步，垂线L1与垂线L2的交点就是所求M的运动轨迹；

第五步，将位于直线L上的点P拖动运动，形成点M的抛物线运动轨迹如图2-3所示。

注意事项：随着拖动某个几何对象，已构建的几何关系依旧有效，几何图形从静态变为动态，塑造出一个动态几何环境，将空间变化立体的展现出来。抛物线的实物模型并不容易想到且实现难度较大，充分利用几何画板的动态与追踪功能，可以解决抛物线过程无法呈现的尴尬。

3.借助多媒体开展数学活动

在开展高中数学教学过程中，为进一步培养学生的人文精神，教师应定期开展各种形式的数学活动，吸引学生数学兴趣。例如，教师可以定期组织学生开展趣味数学、数学发展史研讨会、我们生活中那些与数学息息相关的事等各种有趣的数学竞赛或者演讲比赛，还可以组织学生自己动手制作一些数学模型、数学手抄报等，吸引和培养学生的数学兴趣，帮助学生增长数学见识。在日常教学过程中，教师还可以利用课余时间为学生讲一些有趣的数学故事、相声等，使学生深入体会到数学的乐趣和故事之后的深刻意义，帮助学生进一步开拓数学知识面。例如，在学习“棱锥与棱柱”知识点时，教师可以先利用实物和图片为学生展示棱柱和棱锥在现实生活中是一个什么样的结构和存在，然后让学生利用硬纸片自己动手制作一个棱柱体和棱锥体，将课本上抽象的知识点利用现实生活中的实物展现出来，使其更加形象生动，便于学生理解和掌握，从而进一步培养学生的人文精神。

三、结语

总而言之，高中数学教学中充分发挥多媒体技术，可以辅助教学早日完成目标，提高教学质量，推动高中数学教学效率提升。新形势下融合高中数学与多媒体技术，符合新课改的要求，具有推广价值。