铁路罐车内液体晃动等效力学模型对比分析

张济民，曹玉梦

(同济大学 铁道与城市轨道交通研究院，上海 201804)

液固耦合振动广泛存在于铁路运输中，罐车在运动中与流体晃动相互作用，可能出现车轮脱轨甚至列车倾覆事故[1]。例如，2013年10月21日，合肥东站36 178次货车5节罐车脱轨，其中3节罐车颠覆倾翻，罐内有毒易燃品“己二腈”有泄漏迹象，铁路部门与公安消防部门全力进行处置。类似事故近年来已发生多起。因此，充液罐车动力学仿真计算的精确度需要提高，特别是罐车内液体非充满状态时，液体的晃动对列车运行平稳性、安全性大有影响[2−3]。对于液体−罐体系统，当液体完全填充容器时液体可以等效为刚体模型；当液体有较大自由表面时液体产生多个固有频率的晃动，故需要建立新的等效力学模型。可以用线性动力系统来代替液体线性晃动的动态影响[4]，比如弹簧质量系统或单摆系统。本文中罐体由于其强度高变形微小，分析中将其简化为刚体；液体的晃动分别用弹簧质量模型、单摆模型进行等效力学模拟，将流体的影响近似为弹性振动加入动力学仿真模型中，从而实现流体和结构的耦合分析[5]。

1　液体晃动等效力学模型

目前，适用于铁路罐车内液体晃动的等效力学模型有弹簧−质量模型和单摆模型 2种，而且等效模型的参数仅取决于罐体的形状以及流体的属性。等效力学模型的构建主要基于动态等效，包括构件的力和运动、晃动频率以及质量和惯性参数的类似。

1.1　弹簧−质量模型

在小幅晃动的情况下[6]，弹簧-质量模型能够较好地反映出液体晃动的线性特征，图1为液体晃动前2阶模态弹簧−质量模型原理图[7]。

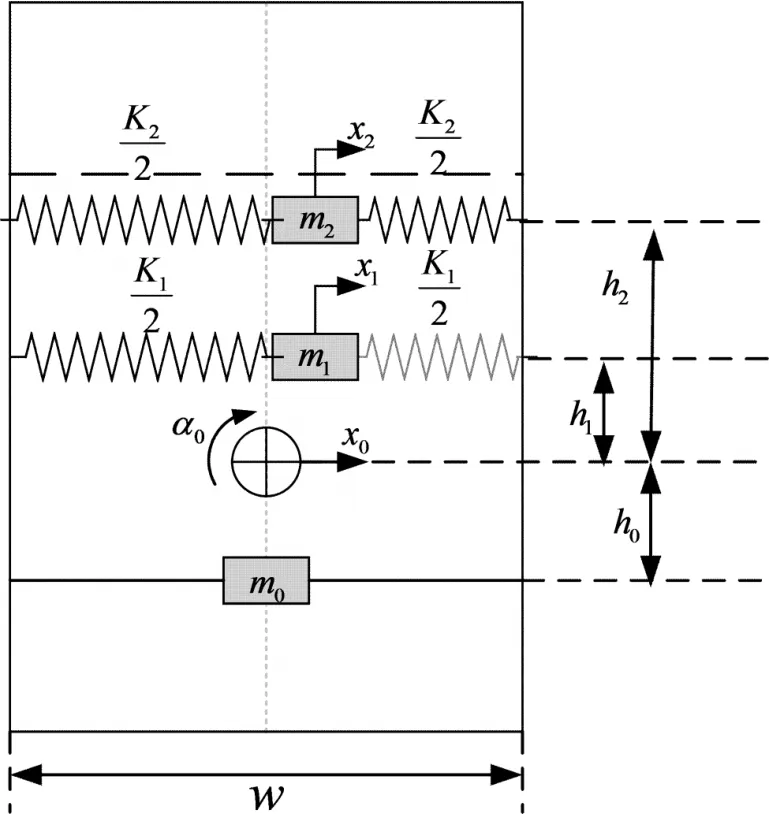
图1　液体晃动前2阶模态弹簧−质量模型原理图Fig.1　Schematic diagram of spring mass model with two modes of liquid sloshing

图中：m1和m2称为晃动质量，m0为固定质量，hi为 mi(i=1, 2)到液体质心的距离，h0为m0到液体质心的距离，w为储液容器宽度，x0和α0为液体质心的位移和旋转角度，xi为质量mi的位移。

1.2　单摆模型

单摆模型就是将液体的每一阶晃动质量简化为一绕固定悬挂点晃动的单摆，其基本原理如图 2所示[8]。

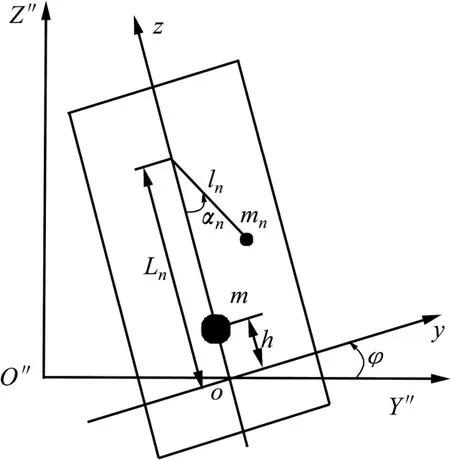
图2　单摆模型原理图Fig.2　Schematic diagram of pendulum mode

图中，m为不参与晃动的液体质量，即刚性质量，到参考面的距离为h；mn为第n阶模态的晃动质量，体现了对应模态的能量水平，是影响晃动力幅值的主要参数；第n阶模态晃动质量的悬挂点距离参考面距离为Ln；ln为无质量摆臂的长度，表征惯性加速度对模态的频率的影响。

2　铁路罐车流固耦合振动模型解析推导

2.1　等效力学模型参数推导

下面以弹簧−质量模型为例分析如何确定模型参数。首先应满足构建等效力学模型的基本原则：等效系统的总质量及质心位置与流体保持一致；流体晃动频率与等效系统固有频率一致；二者产生的作用力及作用力矩一致。

对于每一组弹簧质量系统有以下运动学关系：

罐体的加速度可以假设为在频率Ω处的晃动，则运动学关系可以表示为：

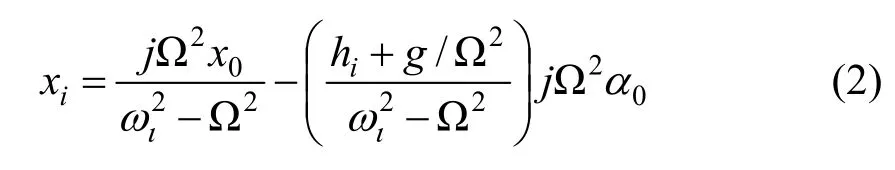
施加在罐体上的沿x方向的力F为：

罐体上绕y方向的力矩M为：

流体晃动所产生的沿x轴方向的力为：

流体晃动所产生的绕y轴方向的力矩为：

根据式(1)～(7)，可推导出：

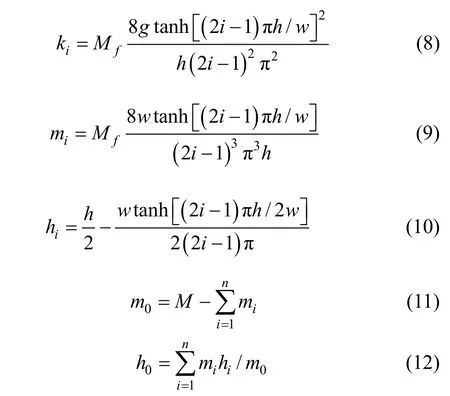
上述表达式表明，模型参数与输入激励的振幅和频率无关。任何周期性激励都可以表示为傅里叶谐波形式，所以模型参数是完全独立的，与罐车激励形式无关。此外，由上述表达式可以得知n＞1阶模型的频率比n=1阶模型频率明显要高。对于高阶模型，晃动质量急速减少，当 h=w时，晃动质量m1=0.258 Mf，m2=0.009 6 Mf，m3=0.002 1 Mf。因此通常只有第一阶的低频晃动质量需要考虑[9]。

2.2　等效力学模型参数表

对长12.5 m半径1.5 m的铁路罐车充水横向晃动问题进行模型参数计算，晃动液体被等效为5个弹簧质量块或单摆，沿罐车长度均匀分布。计算得到不同充液比下，等效力学模型的各项参数，结果如表1和表2所示。

表1　不同充液比液体横向晃动弹簧-质量模型参数Table1　Parameters of transverse sloshing spring-mass models in different liquid-filling ratios

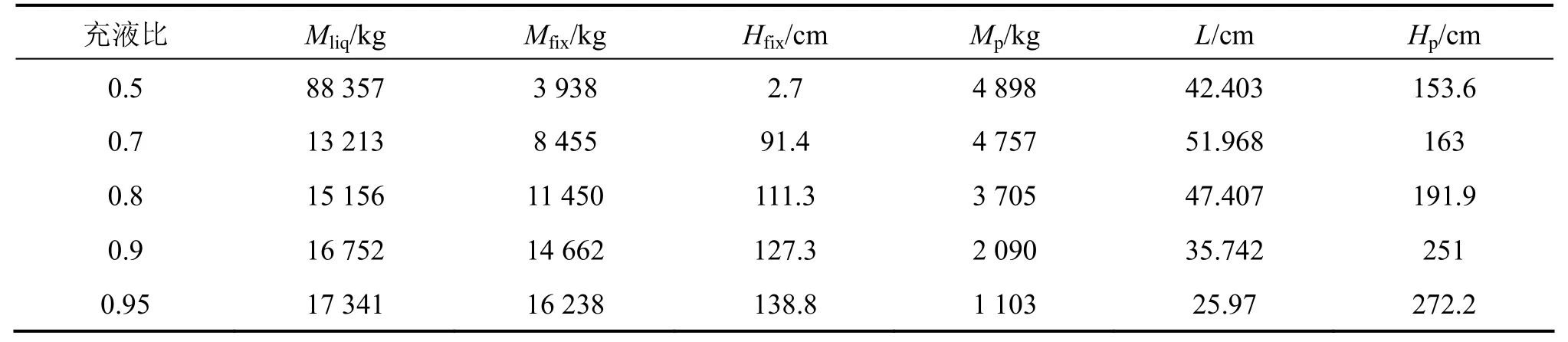
表2　不同充液比液体横向晃动单摆模型参数Table2　Parameters of transverse sloshing pendulum models in different liquid-filling ratios

3　罐车运行安全性数值计算与分析

在动力学建模仿真软件中建立流体−罐车动力学模型，其中流体分别等效为刚体、单摆和弹簧−质量模型。在曲线、道岔工况下进行动力学仿真，分析罐车的动力学特性及安全性。

3.1　罐车曲线运行安全性数值计算与分析

以罐车通过300 m半径曲线为例，在不同充液状态下罐车的脱轨系数和轮重减载率如图3和图4所示。

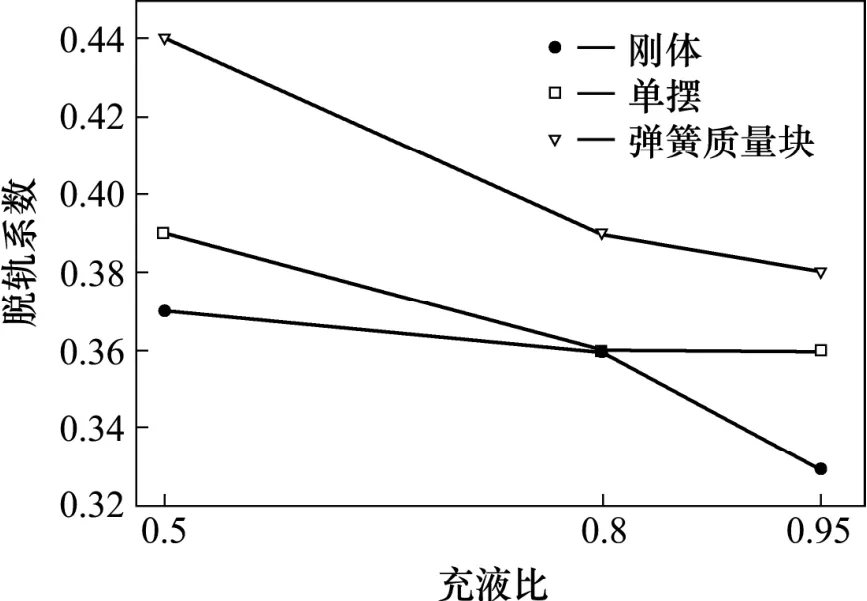
图3 不同充液比下罐车过300 m曲线脱轨系数Fig.3　Derailment coefficient of tanker on 300 m radius curve in different liquid-filling ratios

图3中，刚体模型的脱轨系数计算结果最小，弹簧质量块模型的结果最大。由于刚体模型不考虑液体晃动的影响，使得脱轨系数偏于安全，不能够准确地分析罐车运行的脱轨系数；而单摆和弹簧质量块模型考虑液体晃动后脱轨系数变大，表明液体晃动的影响不可忽略。从图中可以看出，充液比为0.5时脱轨系数最大最危险。

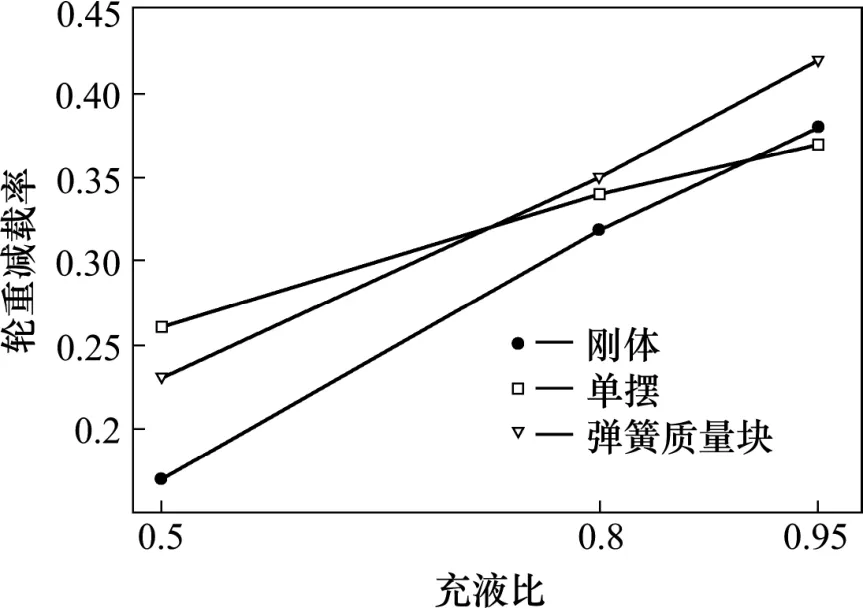
图4 不同充液比下罐车过300 m曲线轮重减载率Fig.4　Wheel unloading rate of tanker on 300 m radius curve in different liquid-filling ratios

图4中，充液比为0.5，0.8时刚体模型轮重减载率计算结果最小；充液比为0.95时刚体模型与单摆模型结果接近，弹簧质量块模型结果最大。

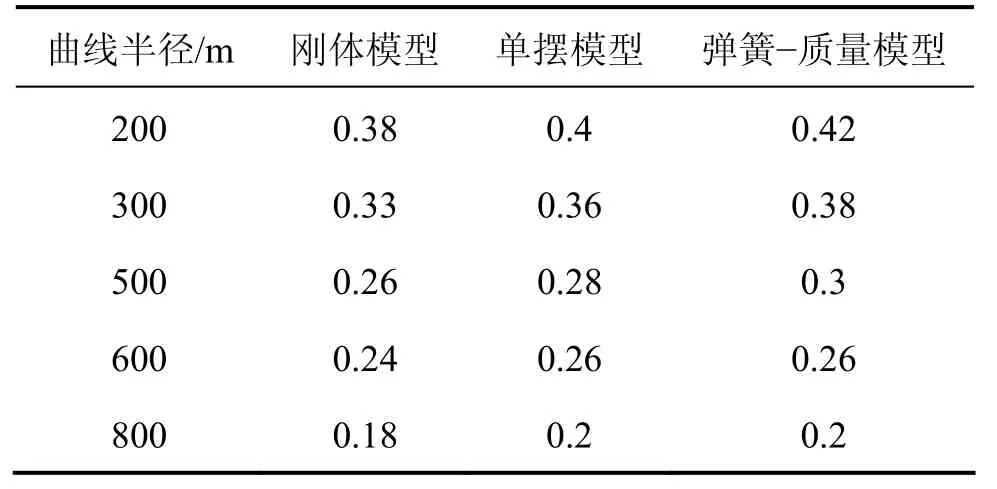
表3　充液比0.95罐车过不同半径曲线脱轨系数Table3　Derailment coefficient of tanker on different radius curves with liquid-filling ratios 0.95

表3中列出了不同曲线半径200～800 m的仿真分析结果，可以看出，结论与罐车过300 m半径曲线时一致，刚体模型脱轨系数偏于安全。

3.2　罐车道岔运行安全性数值计算与分析

罐车以不同速度通过 12号道岔时的轮重减载率如表4所示。

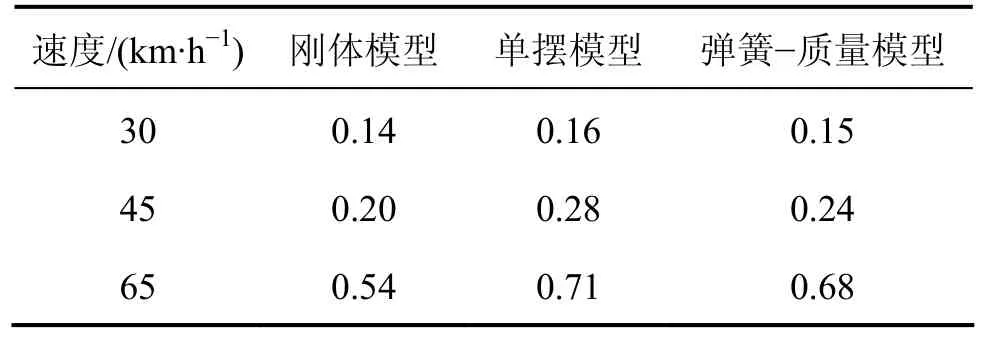
表4　充液比0.95罐车过道岔轮重减载率Table4　Wheel unloading rate of tanker through the switch with liquid-filling ratios 0.95

从表4可以看出，罐车以低速或正常速度通过道岔时，3种模型的轮重减载率未超出限度，其中刚体模型计算结果最小；当罐车以65 km/h速度通过即处于危险工况时，单摆模型和弹簧-质量模型结果均超出了危险限度，而刚体模型结果仍偏安全，不能预估脱轨风险。

以罐车在50 km/h速度下过道岔为例，给出不同充液状态下罐车的脱轨系数和轮重减载率，结果如图5和图6。

图5 不同充液比下罐车过道岔脱轨系数Fig.5　Derailment coefficient of tanker through the switch in different liquid-filling ratios

图5中，当充液比为0.5及0.8时，液体的晃动作用影响较大，刚体模型不能将液体对罐车的横向作用力等效，脱轨系数偏小；充液比为0.95时，液体晃动幅度较小，3种模型脱轨系数无明显差距。

图6中，在罐车以50 km/h速度通过12号道岔的危险工况下，刚体模型轮重减载率计算结果未超出危险限度，显示安全；单摆和弹簧质量块模型在充液0.8及0.95时超出危险限度，表示有脱轨风险。

图6　不同充液比下罐车过道岔轮重减载率Fig.6　Wheel unloading rate of tanker through the switch in different liquid-filling ratios

4　结论

1) 弹簧质量模型和单摆模型所得到的计算结果大于刚体模型。所以不考虑液体晃动的刚体模型不能准确进行罐车安全性分析，特别是当充液比较小时，液体晃动的影响不可忽略。

2) 对罐车内液体晃动等效力学模型的对比分析表明，在将来罐车的建模分析中，可以借助单摆模型、弹簧质量块模型对流固耦合的作用进行等效，其结果更加准确，具有重要的工程实际意义。