三维一阶速度—应力声波方程全波形反演

李海山 杨午阳 雍学善

(中国石油勘探开发研究院西北分院，甘肃兰州 730020)

1 引言

随着地震勘探的深入，逆时偏移等深度域成像技术得到了快速发展，但这些方法的成像质量很大程度上取决于速度模型的精度[1，2]。目前存在大量的速度建模方法，如叠加速度分析、偏移速度分析、旅行时层析反演和全波形反演方法等[3]。全波形反演(Full waveform inversion，FWI)充分利用了地震波的运动学和动力学特征，通过最优化算法不断地更新介质参数模型，使模拟地震记录与实际观测地震记录之间的残差达到最小，从而得到与实际介质参数最接近的模型[4]。相对于旅行时层析等方法，FWI精度更高，不仅能够满足复杂构造成像方法对速度参数的精度要求，而且具备岩性反演与储层预测的潜力[3，5]。

自从Tarantola[6]和Mora[7]提出FWI方法以来，众多学者致力于该类方法的理论及应用研究，已被广泛应用于海上资料[4，8]，并逐渐应用于陆上资料[9，10]。FWI包括三个关键环节，即炮点正向传播波场和检波点逆时传播残差波场的计算、模型参数梯度(或Frechét导数)的计算和模型参数的更新，其中梯度计算是最关键的环节，梯度的计算方式及精度决定了反演的计算量及收敛性。由于直接求取Frechét导数往往较困难，需要巨大的计算量，因此许多学者采用间接方法避免Frechét导数的直接求取，如Tarantola[6]利用格林函数法推导出目标函数关于地下介质参数的梯度。伴随状态法是求解目标函数关于模型参数梯度的有效方法之一，已广泛用于地球物理反演问题的求解[11，12]。胡光辉等[13]利用伴随状态法导出了频率域梯度计算公式，实现了时间域正演与频率域反演相结合的三维声波FWI。

FWI可在不同域中实现，如时间域[6，7]、频率域[14，15]和拉普拉斯域[16]等。尽管在频率域可实现从低频到高频的多尺度FWI，但频率域正演内存需求巨大，特别是三维情况下矩阵求逆运算对于内存需求极高，甚至难以实现[17]；与频率域反演方法相比，拉普拉斯域反演方法不易陷入局部极值，对初始模型的依赖程度更低，但只能恢复模型中的长波长构造信息，对模型细节的刻画能力不足[18]。由于在不同域中实现FWI具有不同的优缺点，因此出现了将各自优点相结合的混合域FWI方法，如时间—频率域[14，19]、拉普拉斯—频率域[18]、时间—拉普拉斯—频率域[20]等FWI方法。

尽管时间域反演方法由于同时反演所有频率成分，增大了问题的非线性程度，对初始模型的依赖性较强，但实际资料反演表明反射层析初始建模与时间域多尺度反演策略相结合可以显著降低这种影响[21，22]； 此外，时间域波场正向传播及逆时外推时较直接、快速，可以更好地估计震源的延迟时间，可以灵活地对数据进行必要的预处理； 同时，时间域正演可以方便地使用震源并行算法，能够较好地适应各种采集系统。

综合前述分析，本文基于三维一阶速度—应力声波方程，采用基于摄动理论的伴随状态法，推导出时间域三维一阶速度—应力声波方程的伴随方程及相应的纵波速度的梯度计算公式； 在此基础上实现了时间域三维声波FWI，并通过模型数据检验了方法的可行性和有效性。

2 全波形反演目标函数

非均匀各向同性介质中，三维声波方程的一阶速度—应力方程为[23]

(1)

式中：p为压力场；vi(i=x，y，z)为波场速度分量；ρ为介质密度；fp为震源项；K为体积模量，与纵波速度V的关系为

K=ρV2

(2)

全波形反演是利用全波场信息，通过优化方法估计地下介质参数模型，使正演地震记录与观测地震记录达到最佳拟合[5]。设目标函数为波场残差能量，即

δ(x-xr)dΩdt

(3)

式中：u(m；x，t)为正演地震记录；T为地震记录长度；uobs(x，t)为观测地震记录；m为模型参数向量；u=(vx，vy，vz，p)T为地震波场向量；xr为接收点位置；Ω为模型的边界。

利用FWI方法求取地下介质模型参数时，如果采用局部最优化方法，例如共轭梯度法，需要计算目标函数对模型参数的梯度，且反演结果的有效性依赖于梯度的有效性和准确性。自Plessix[11]将源于控制论的伴随状态法引入反演问题，许多学者将该方法引入地球物理反演问题的求解，用于计算依赖于一组状态变量的目标函数的梯度[24]。依据伴随状态法原理，对式(3)施加式(1)的约束，可以得到如下的最优化问题

(4)

式中：λ(x，t)=(λx，λy，λz，λp)T为伴随波场向量；E(m)=0为式(1)的简写形式。

3 伴随方程及模型参数梯度

将式(4)展开，有

(5)

令式(5)对地震波场向量的偏导数为零，即

(6)

结合边界条件

(7)

及终止条件

(8)

可以得到下面的伴随方程(详细推导见附录A)

(9)

该方程即为波场残差从检波点位置开始的逆时反传方程。

式(5)对体积模量K求偏导，可得

(10)

定义分辨率核函数为

(11)

式(11)即为体积模量的梯度计算公式。由式(2)可得关于纵波速度的梯度计算公式为

(12)

考虑到地震成像中速度模型为首要需求，本文暂不考虑密度变化的影响，即只进行三维常密度声波方程的FWI。

4 全波形反演策略

目前多采用局部优化反演方法使目标函数达到最小[25]。在局部最优化方法中，虽然共轭梯度法只利用一阶导数信息，却克服了最速下降法收敛慢的缺点，避免了牛顿法需要存储和计算Hessian矩阵并求逆的缺点，因此得到广泛使用[3，26]。共轭梯度法的基本思想是利用目标函数上某一点的梯度构建出一组共轭方向，沿着共轭方向进行搜索，寻求目标函数的极小值点。共轭梯度法纵波速度更新的表达式离散化后写成向量形式为

Vn+1=Vn+αφn

(13)

式中：n为迭代次数；α为共轭方向上的搜索步长；φn为共轭方向，即

(14)

式中βn为标量参数。共轭梯度法根据βn的不同求取形式分类，本文采用Fletcher-Reeves方法计算[26]

(15)

共轭方向上的搜索步长α对反演收敛有重要的影响，步长过小会增加迭代次数、降低反演效率；步长过大易导致反演陷于局部极值。通常采用线性搜索方法和抛物线拟合法确定模型参数更新步长，抛物线拟合法需要额外的二次正演模拟，因此本文采用非精确线性搜索方法求取步长[27]。

在每次迭代过程中，炮点正向传播波场用式(1)计算，检波点逆时传播残差波场用式(9)计算，用式(12)计算纵波速度梯度，接着用式(13)更新纵波速度模型。由于交错网格有限差分法比中心网格有限差分法具有更好的数值频散抑制能力[24]，因此波场传播采用交错网格有限差分法模拟；此外，在时间域波场传播较直接、快速，结合GPU并行计算的优点[28]，可以显著提高计算速度。

5 模型测试

3D SEG/EAGE逆掩推覆速度模型纵向层位多且具有强烈的横向速度变化，可以用于验证FWI的适应性，检验FWI对断层、河道等细节的刻画能力。考虑到计算量和单个GPU节点的内存限制，在测试时对3D SEG/EAGE逆掩推覆速度模型相关参数进行了修改(图1)，其中网格数为160×160×120，空间步长为15m。

采用正交观测系统，利用速度模型(图1)生成三维声波观测记录，震源子波是主频为15Hz的雷克子波，炮点与接收点均置于地表，共激发256炮进行全方位接收，每炮160×160个检波点，炮点距和炮线距均为150m，检波点距和检波线距均为15m，记录长度为1.5s，时间采样间隔为1ms，最大炮检距为3400m。反演初始速度模型通过三维高斯平滑得到，共迭代60次得到最终反演结果。

图1 3D SEG/EAGE速度模型

图2为225m深度反演速度切片，可见反演后构造边界， 特别是浅层河道边界及内部速度结构得到了准确刻画。图3为375m深度反演速度切片，尽管初始模型严重偏离准确模型，但反演后断层及局部细节都得到了准确刻画。需要注意的是，在图2和图3中，边界区域的速度反演精度远低于中心区域，主要是受覆盖次数低及炮检距较小的影响。

图4为第80条联络测线准确速度、初始速度及反演速度剖面对比，可见浅层河道、构造等得到了较好刻画，而随着深度的增加，反演准确性逐渐降低，部分原因是深层反射能量不足，另一原因是需要采用更优的梯度预条件算子及梯度更新优化方法提高反演精度[29]。同时可见，逆掩推覆体右侧陡倾构造的反演精度高于左侧， 这是因为逆掩推覆体右侧的观测炮检距更大，为陡倾构造的反演提供了更好的照明。因此，FWI要求尽可能提供宽方位大炮检距资料。

图2 真实速度(a)、初始速度(b)和反演结果(c)225m深度切片对比

图4 真实速度(a)、初始速度(b)和反演结果(c)第80条联络测线对比

图5为(0.9km，0.9km)、(1.2km，1.2km)及(1.5km，1.5km)三个不同位置准确速度、初始速度及反演速度单道曲线对比，由于(0.9km，0.9km)处于逆掩推覆复杂构造上，反演速度曲线与准确速度曲线偏差较大(图5a)；(1.2km,1.2km)、(1.5km,1.5km)位置处于逆掩推覆复杂构造翼部，反演速度的准确性明显提高(图5b、图5c)。下一步，可以通过实现基于模型分割的GPU/CPU异构协同并行反演方法突破计算和内存的限制，增大模型和炮检距提高复杂高陡构造区的速度反演精度；同时，为提高反演曲线(图5)低频趋势的准确性，可采用时间域多尺度反演策略。

图6为FWI时归一化波场残差随迭代次数变化曲线，可见本文反演方法稳定性和收敛性均较好，迭代60次后观测记录与拟合记录之间的残差较小。需要注意的是，本文反演中采用准确子波，反演方法的噪声抑制能力也有待提高。为进一步提高反演方法的性能，可采用褶积型目标函数[30]，并引入模型参数的正则化项[31]。

图5 不同位置真实速度(蓝线)、初始速度(黑线)和反演结果(红线)单道曲线对比

图6 归一化波场残差随迭代次数的变化曲线

本文方法基于GPU在时间域实现，相比单节点CPU，波场正向传播及逆时外推时较直接、快速。表1给出了模型网格数不同时单个CPU与GPU的正演计算时间对比，表2给出了单节点上GPU卡的数量与正演计算时间对比(GPU卡为Tesla K10)，可见，与CPU相比，GPU具有较高的计算效率，尤其是对于较大模型的三维FWI。

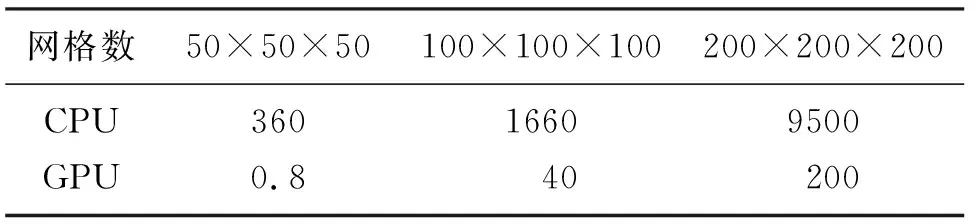
表1 单个CPU与GPU的正演计算时间(s)对比

表2 不同GPU卡数量的正演计算时间(s)对比

6 结论

本文采用基于摄动理论的伴随状态法，实现了基于一阶速度—应力声波方程的三维全波形反演方法。具体计算时，炮点正向传播波场用时间域三维一阶速度—应力声波方程计算，检波点逆时传播残差波场用推导出的伴随方程计算，波场传播采用交错网格有限差分法模拟。模型测试结果证明了方法的可行性和有效性。

本文方法由于在时间域实现，波场正向传播及逆时外推时较直接、快速，结合GPU并行计算的优点，可以显著提高计算速度。本文方法只是实现了在单个节点上多个GPU卡的并行计算，在计算效率、反演准确性的提高、对噪声的抑制能力、对实际资料的适应性等方面有待进一步改进。

附录A 伴随方程的推导

式(5)对波场速度分量vx求导，可得

(A-1)

对上式分部积分，有

(A-2)

式(A-2)满足终止条件及边界条件：λx|t=T=0，λp|x=x1=λp|x=x2=0，其中x1和x2分别为地下介质参数模型在x方向的两个边界。结合终止条件及边界条件，式(A-2)可以化简为

(A-3)

同理，式(5)对速度分量vy和vz求导，结合终止条件及边界条件，可得

(A-4)

(A-5)

式(5)对压力场p求偏导，可得

(A-6)

对式(A-6)分部积分， 结合终止条件及边界条件：λp|t=T=0，λx|x=x1=λx|x=x2=0，λy|y=y1=λy|y=y2=0,λz|z=0=λz|z=Z=0, 其中y1、y2和Z分别为地下介质参数模型在y方向的两个边界和在z方向的下边界，得

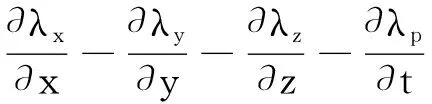
(A-7)

令式(A-3)、式(A-4)、式(A-5)和式(A-7)等于0，可得伴随方程(式(9))。