潜在类别模型和主成分法在稀有变异关联分析中的应用比较*

皮路程　卜　涛　冀晓慧　赵　丽　李丽霞　刘　丽　郜艳晖

广东药科大学公共卫生学院统计学教研室(510310)

【提　要】　目的　比较潜在类别模型和主成分法在稀有变异遗传关联研究中的统计性能。方法　利用GAW17数据库,通过集合策略将同一基因中的稀有变异合并成一个新变量,以基因为分析单位,分别运用潜在类别模型和主成分法构建常见变异和集合后稀有变异的分类潜变量或主成分,再应用线性回归模型分析基因对定量性状的整体效应,评价两种方法的I类错误和效能。结果　潜在类别模型的I类错误(0.040～0.085)均不高于主成分法(0.040～0.190)。对强效应的稀有变异和常见变异,即使存在多个无关联稀有变异,潜在类别模型也能很好地分类且效能(1.000)不低于主成分法(0.990～1.000);但稀有或常见变异效应弱时主成分法效能(0.635)高于潜在类别模型(0.200)。对多数非关联基因,潜在类别模型不收敛。结论　和主成分法类似,潜在类别模型也可和稀有变异的集合策略结合,通过构建遗传变异数据的分类潜变量,进行稀有变异的遗传关联研究。分析定量性状时两法均可识别较强效应的稀有变异和常见变异。人群中遗传变异分布无异质性时,潜在类别模型常不收敛,提示遗传变异和性状无关联。

随着二代测序技术的快速发展,大量含稀有变异(rare variants,RV)的遗传数据应运而生。如次等位基因频率(minor allele frequency,MAF)低于5%时,传统关联性分析方法效能极低[1]。近年学者提出将感兴趣区域(region of interest,ROI)内的稀有变异集合(collapsing)再进行后续分析的方法统称为负担检验(burden test)[2-3]。但负担检验常忽视位点间的连锁不平衡,面对存在连锁不平衡的高维遗传数据,Kazma[4]提出潜变量(latent variable)降维的思路,将主成分与集合方法(principal components and collapsing,PCC)结合,以聚集稀有和常见变异的遗传信息来提高分析效能。然而PCC法需假设遗传模式,而以处理分类变量为优势的潜在类别模型(latent class model,LCM)[5-6]基于异质性将人群分类,应用于遗传关联研究时不依赖遗传模式假设,同时达到降维目的。本研究将集合策略与LCM结合,应用于GAW17(genetic analysis workshop 17)数据库[7-8],并和PCC方法进行比较,为稀有变异遗传关联研究提供统计学方法的支持。

材料与方法

1.数据来源

GAW17数据库包含了697 例多种族无血缘个体的常见变异和稀有变异的真实数据,及基于遗传变异基因型和假定的表型关联模拟了3个定量性状(Q1、Q2和Q4)和一个二分类性状(受累与否),协变量包括吸烟状态、性别和年龄。每种表型模拟产生200个数据集。

2.表型和基因位点的确定

本研究将Q1和Q4用于分析,从GAW17数据库选取Q1的遗传变异包括VEGF(vascular endothelial growth factor)通路上的8个基因中38个SNPs。各基因分别包含1～11个功能性变异,其MAFs的范围从0.07%到16.5%。Q1的剩余遗传度为0.44。Q4的遗传度为 0.70,但不受数据库中任何遗传变异的影响。

分析Q1时,选择与Q1关联的基因用于评价效能;同时选取无关联基因用于评价I类错误。由于和Q1关联的基因与Q4无关,因此分析Q4也用于评价I类错误。基因的纳入标准为:(1)同时含常见变异和稀有变异;(2)仅选择包含错义突变 SNPs 的基因。最后纳入四个Q1关联基因(ELAVL4,FLT1,HIF3A,KDR)和四个非关联基因(TMCC1,ZNF493,AKAP7,ALDH1A2)。各基因的常见和稀有变异及效应信息见文献[7],归纳见表1。

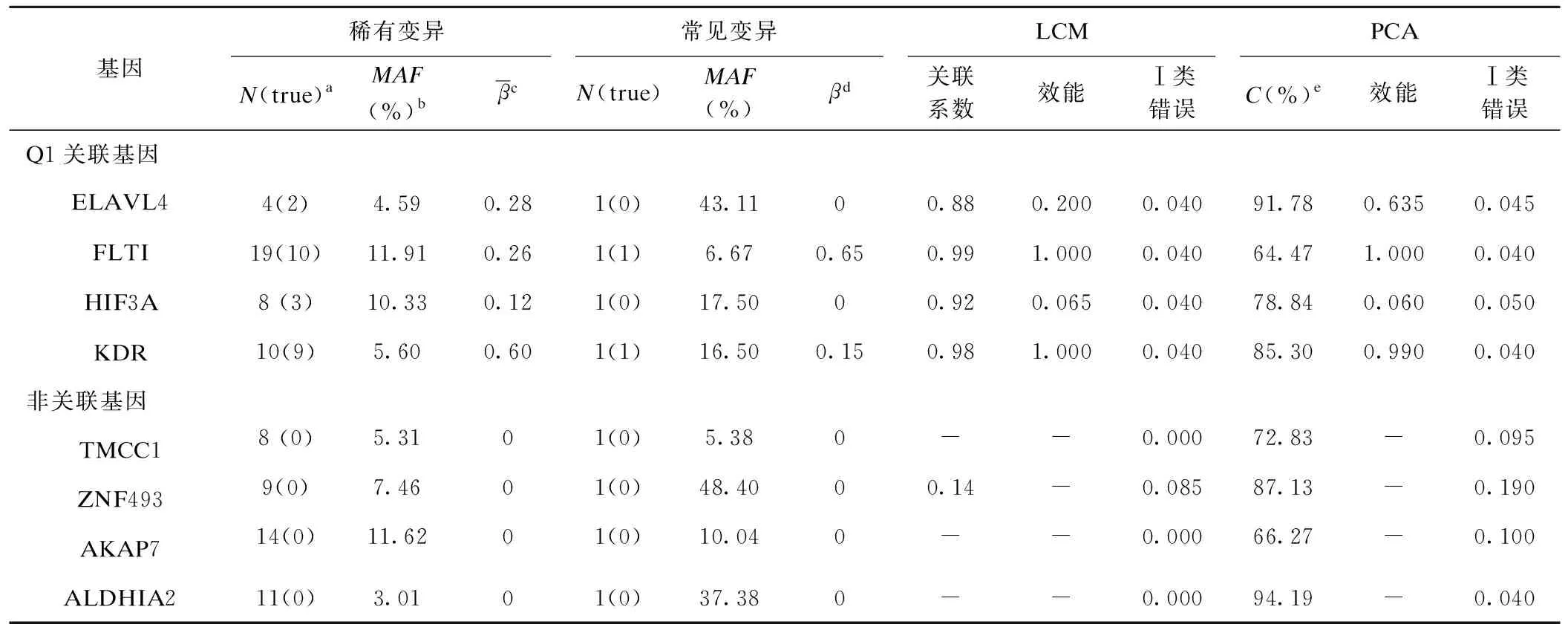
表1　PCA与LCM的统计效能和Ⅰ类错误

a:N(true)为纳入分析的SNPs个数(有关联的SNPs个数);b:F(%):集合后的新变量频率;c:稀有变异平均效应=稀有SNPs的效应之和/SNPs的个数;d:β为常见变异效应值;e:第一主成分解释百分比;

3.分析过程及评价指标

对每个基因中的稀有变异,先采用指示赋值的集合策略将其合并,再与该基因中常见变异一起,分别应用主成分分析(principal component analysis,PCA)和潜在类别模型,得到第一主成份和分类潜变量。将第一主成分或分类潜变量在调整协变量的条件下分别对200次模拟的Q1和Q4拟合线性回归模型,记录每次调整协变量后第一主成分或分类潜变量回归分析对应的P值,分别计算效能和 I 类错误。

主成分分析原理和潜在类别分析原理参见文献[5-6]。LCM最优模型的选择主要依据AIC(LL)和BIC(LL)指标,指标越小说明模型拟合越好,其中LL是指模型适配的对数似然值。

本研究中使用Latent GOLD 4.5[11]完成LCM,其余分析采用SAS 9.2[12]。

结　　果

1.LCM的最优模型分类

Q1关联的四个基因最优模型将人群都分为两类(表2)。在Q1非关联的四个基因中,仅基因ZNF493 可以将人群分为两类,其余三个基因LCM模型不收敛(表3),提示人群在此基因上的分布无异质性。

表2　Q1关联基因的LCM最优模型选择

2.LCM与PCA方法的效能与Ⅰ类错误

四个关联基因中,基因FLT1的常见变异和KDR的稀有变异效应较高,(平均)效应值分别为0.650和0.600,但稀有变异中均混有相当数量的非关联变异,此时PCA和LCM的效能均接近或等于1.000。而基因ELAVL4、HIF3A的常见变异均无效应,稀有变异中前者平均效应为0.28,后者为0.12,且稀有变异中混有一半以上非关联变异,此时PCA效能为0.635和0.060,LCM为0.200和0.065。此外表1也显示每个关联基因中常见变异和集合后的稀有变异有较强的关联,关联系数为0.88～0.99。

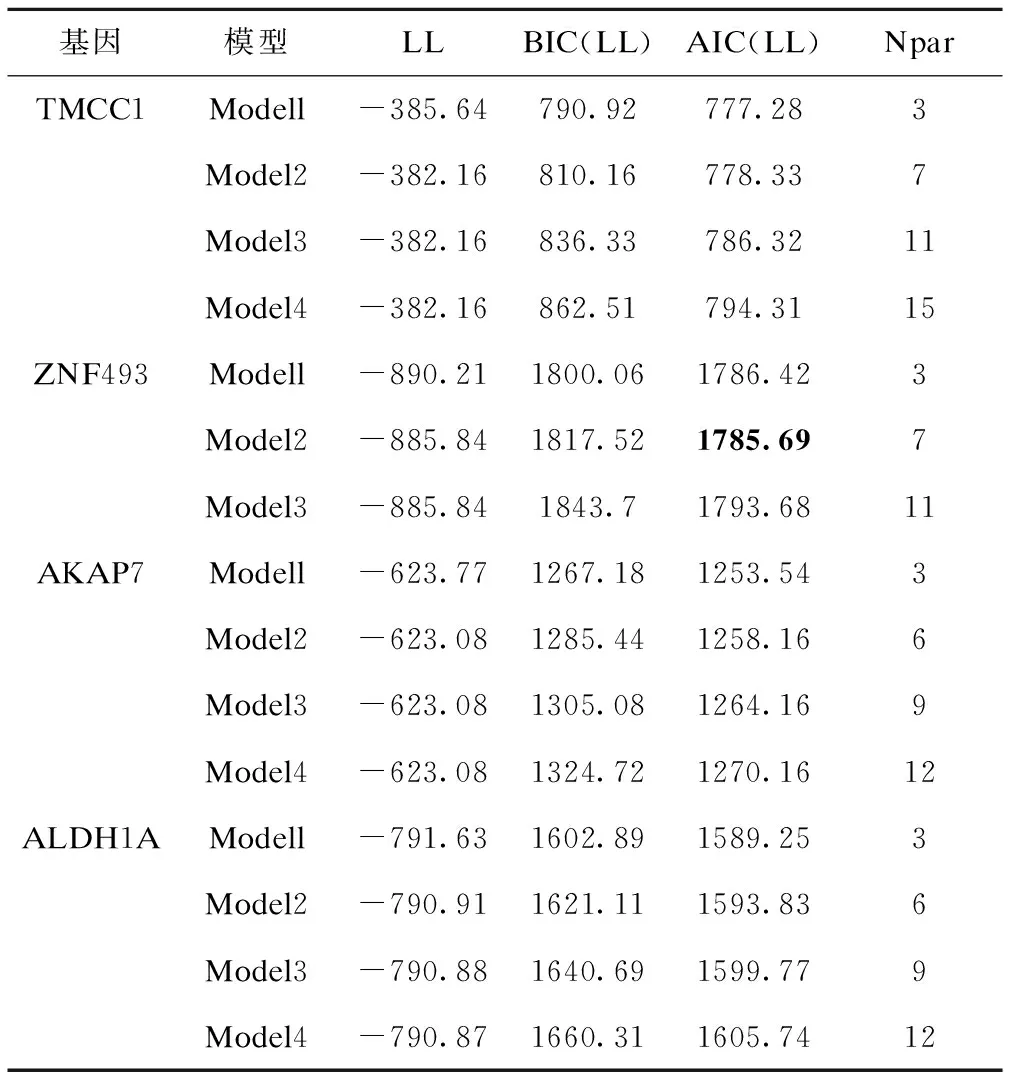
表3　非关联基因的LCM最优模型选择

Q1关联基因的主成分或分类潜变量与Q4表型的200次回归结果显示,两法的Ⅰ类错误均不超过0.05,LCM比PCA法略低。非关联基因中除ZNF493外,LCM结果均未收敛,提示三个基因的分布在病例与对照组中无异质性,但PCA法将分类变量做连续变量处理,第一主成分解释的百分比在66.27%～94.19%之间,可能高估了变异间的关联,各基因Ⅰ类错误见表1。

讨　　论

众多GWAS(genome-wide association studies)研究表明其识别出来的常见变异对于疾病遗传风险的解释仍较低,寻找低频或稀有变异对疾病的贡献是后GWAS时代的重要任务之一,已有研究表明疾病和低频及稀有变异存在关联,且具有很强的效应[9]。但此类遗传数据具有频率低、维度高、为分类变量,且变异间存在连锁不平衡等特点,因此本研究在稀有变异集合策略的基础上,以基因为分析单位,探讨潜在类别模型在稀有变异关联研究中的适用性。

应用集合策略将ROI内的稀有变异合并后再进行关联分析,从而提高稀有变异的频率,增加关联研究的统计效能。目前常用的负担检验有多变异集合法(combined multivariate and collapsing,CMC)[13],考虑变异权重的加权合计检验(weighted sum test,w-Sum)[14]和考虑变异效应方向的SSU (sum of the squares of the marginal score statistics)和SSUw(weighted form of sum of the squares of the marginal score statistics)[15-16]方法。但负担检验并没有考虑连锁不平衡以及基因间的交互作用,而忽视这些遗传结构会导致其统计性能降低,不能很好地反映变异与疾病之间的关联[17]。

本研究采用PCA和LCM法提取主成分或构造分类潜变量进行降维。特别是LCM以处理分类变量为优势,对数据降维的同时更好地了解变异分布,识别不同性状群体间遗传变异分布的异质性。若群体间不存在异质性时,模型不收敛,提示变异与疾病之间没有关联。目前该法在常见变异遗传关联研究中已有应用[18]。本研究将稀有变异的集合策略与LCM结合应用于GAW17数据,结果显示各类情况下,LCM的I类错误均不高于PCA。而稀有变异和常见变异强效应时,即使混有较多无关联变异,LCM仍可很好地对观测进行分类,且效能不低于PCA;但稀有或常见变异弱效应时效能不高,这可能与稀有变异频率或集合时混杂较多的无关联变异有关。本研究采取指示赋值的集合策略,并没有考虑稀有变异的方向以及权重,此外,LCM要求满足局部独立性假设,即在给定的潜在类别下显变量之间相互独立,否则可在模型中加入直接效应变量、删掉冗余的外显变量或采用潜在类别因子分析构建模型等[19],更多的理论和应用需要进一步研究。