单样本率比较(单组目标值法)的样本量计算及其简便实现
曾治宇 林 娜 张明东 Peter Lam
样本量计算是临床研究设计阶段的主要工作之一,其重要性在国内日渐受到重视,为此在2015年还发表了一个《临床试验中样本量确定的统计学考虑》的专家共识[1]。
目前临床研究中,特别是医疗器械的临床研究中,单组目标值法(performance goal,PG)的应用越来越多。事先确定一个目标值(目标值的确定必须谨慎,依据充分,但这个不在本文的讨论范围内),将研究预计能够达到的值与之进行比较。例如美国FDA对于射频消融导管的建议为急性成功率、慢性成功率及主要并发症的目标值分别为85%,80%及7%,而预计值分别为95%,90%及2.5%。国内CFDA也开始将这一方法写入一些医疗器械临床试验的指导原则中。
对于计数资料的单组目标值法,从统计学角度来看其实就是单样本率的比较。如果进行确切计算将涉及到二项分布,手工计算困难,常需借助特殊软件。本文拟结合文献发表的实例,介绍常规软件excel及免费软件G*Power进行单样本率比较的样本量计算。
计算方法
单样本率比较的样本量计算常见的方法为正态近似法(公式1[2]),适合目标事件发生率不太极端且样本量足够大时,否则应进行平方根反正弦变化(公式2[3])。我们将这两个公式分别输入excel表中,其中的参数可替换为实际的单元格引用,便于重复使用。
(1)
(2)
根据二项分布进行确切计算时使用G*Power免费软件,上文提到的专家共识[1]也有此推荐。G* Power是由德国杜塞尔多夫大学开发的软件,包括的样本量计算系列有Exact、Ftest、ttest、χ2test及ztest等,本文使用的版本为3.1.9.2。
实例分析
某临床试验欲验证一款彩色多普勒超声系统的临床有效性,采用标准对照设计,用图像优良率为主要评价指标,临床有效的标准为图像优良率不低于85%。预期试验机器的图像优良率为95%,以0.05为检验水准,采用双侧检验,设定检验效能为80%,试估计样本量[2]。该文献利用nQuery计算的结果为79,SAS计算结果也是79,我们根据公式(1)利用excel正态计算的结果为78.017,如果向上取整,也是79。该例中预期的率达到95%,已经不太适合正态近似法了,但该文并未给出利用二项分布确切计算的结果。在另一篇文献[4]对于同一实例利用SAS逐步寻值法编程得到的样本量为75,我们利用G*Power直接计算的结果也是75,但利用post hoc根据检验功效决定的样本量为84。我们在下一个例子中对G*Power软件的计算作些具体的说明。注意如果用公式(2)利用excel反正弦计算的结果是67,差异较大,我们在下文会有讨论。
为验证某一治疗肝癌的组合治疗方案是否有效,拟进行临床试验设计。根据以往研究数据获知,肝癌的5年生存率为50%,研究者预期新的组合治疗方案能使肝癌的5年生存率提高至60%,试按照检验效能为80%、检验水准为0.05的双侧检验估计本试验所需样本量[2]。文献对此进行了确切概率检验,利用nQuery软件时,在相应的窗口内样本量一行反复尝试填入不同数据,直至获得检验效能达到或超过80%,得到样本量为208。SAS编程运算的结果也是208。我们根据公式(1)利用excel正态计算的结果为194,根据公式(2)利用excel反正弦计算的结果也是194。使用G*Power直接计算的结果为199,此时的检验功效为0.804,但α仅为0.047;使用G*Power post hoc计算样本量为194时的检验功效为0.764,但α仅为0.037。这个例子中的率不极端,样本量也较大,因此正态法、反正弦法及G×Power软件直接计算的结果较为一致。
G*Power还可方便地给出在指定的α水平下(如α≤0.05),设定一定范围内不同样本量(例如此例设定样本量的范围为180~220)时的检验功效(图1)。图1中可以清晰地看到,横坐标样本量194对应的纵坐标检验功效只有0.764,虽然样本量199时的检验功效为0.804(此时的α=0.047),但样本量增加至200时的检验功效反而降至0.787(注意此时的α=0.040)。只有样本量达到210时,检验效能才稳定地居于0.8之上,因此根据post hoc的结果这个例子的样本量计算结果为210,与上面nQuery与SAS的结果基本一致。
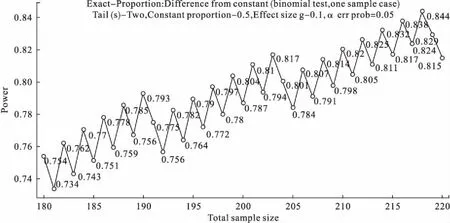
图1 G*Power软件post hoc给出特定样本量下的检验效能
本文写作之际,国家食品药品监管总局于2017年1月4日发布了《人工耳蜗植入系统临床试验指导原则》,关于样本量的描述如下:根据临床经验,开机12个月后,产品的总体有效率需至少达到70%(目标值为70%)方可被临床接受。假设被试验产品的总体有效率可以达到85%,则在双侧显著性水平0.05、把握度80%的情况下,至少需要64例患者,考虑10%的脱落率,共需要70例患者[5]。
该文件未说明具体的计算方法及应用的软件,我们利用excel根据公式(1)正态近似法计算的结果正好是64例,而根据公式(2)平方根反正弦变化计算的结果为60例。而利用G*Power软件精确计算的结果为70例。
讨 论
在率不是过大或过小的情况下,单样本率比较样本量计算的正态近似法基本可行,excel输入公式后计算简洁明快。确切计算时,免费的G*Power软件能方便地给出不同样本下检验功效值,图形显示直观清晰,甚至优于nQuery与SAS的表达,也比既往文献[4,6]推荐的方法简洁得多。
值得注意的是,由图1可见,确切计算样本量时,随着样本量的增加,检验功效不是单调增加的。大家熟知的正态分布函数是连续的,在给定α水平时,随着样本量的增加,检验功效随着增加。而基于二项分布的计算是非连续的,也就是说在不同的样本量下,α值和β值是跳跃变化的。为了保证满足α≤0.05的要求,样本量增加时,α值可能会变小,这时1-β(即检验功效)也可能跌至既定的值如0.8以下。检验功效和样本量的关系尽管总的趋势仍然是递增的,但表现为锯齿状递增,不是纯粹的单调递增关系。例如例2在样本量199时的α值为0.047,检验功效为0.804;在样本量增至200时,α值降至0.040,检验功效下降至0.787,低于0.8。这也提示在利用类似二项分布这种非连续分布模型进行样本量计算时,要考虑到样本量变化与检验功效变化的这种关系,在局部情况下,样本量增加,检验功效反而是下降的。因此,对于实例1,文献利用SAS编程得到样本量75是值得商榷的。临床研究设计时,特别是在样本量较小的确证性临床研究中,务必反复权衡,避免设计失误。

