曲线型树状柱计算长度和稳定性分析研究
杨建林 周 强 王 锦 沈 炜
(1.江苏城乡建设职业学院,常州 213147; 2.谢亿民工程科技(常州)有限公司,常州 213000)
0 引 言
树状结构是一种具有自然界树木的形状且具备一定支承作用的空间结构。最初是由德国建筑师Frei Otto于20世纪60年代提出,具有多级分支、三维伸展的几何特点,分支覆盖范围广[1]。因此,在不影响使用功能的前提下减少了上部水平构件的跨度,使受力更均匀。树状柱根据杆件曲直可分为两类,一类是直线型树状柱,如图1的斯图加特机场候机厅,采用了三级分叉的树状柱,图2的深圳文化中心“黄金树”,结构非对称不规则,此外还有长沙南站、徐州东站、深圳北站等国内高铁站候车站台采用的树状柱;另一类是曲线型树状柱,如图3的孟买宴会厅,由主干伸出一级曲线分支,再由一级分支伸出多根直线分支,每一分区的树枝杆件在同一竖平面内,图4的芝加哥某公园太阳能遮阳棚,仅有一级曲线分支,分支在竖平面内单向弯曲。

图1 斯图加特机场候机厅Fig.1 Departure hall of Stuttgart

图2 深圳文化中心“黄金树”Fig.2 Golden Tree of Shenzhen culture center

图3 孟买宴会厅树状结构Fig.3 Dendritic structure of Bombay banquet hall
树状柱作为结构的主要支承构件,其稳定性分析和计算长度确定是必要的。构件和结构的稳定问题是一个整体性问题,结构的稳定由构件的稳定性决定,而构件的稳定取决于构件本身几何形状、相邻构件对其的约束以及荷载的分布。合理的稳定性分析方法和计算长度确定方法对于曲线型树状柱在工程中的运用具有重要意义。
文献[1]通过有限元软件ANSYS,在树状柱杆件上施加一对集中力,来进行线弹性屈曲分析,然后根据欧拉公式反算计算长度系数,给出了树状柱构件计算长度系数取值建议。文献[2]以一个六柱支承的圆形屋盖结构为例,进行了考虑材料和几何非线性的屈曲分析,研究了该结构的稳定性;然后采用整体模型提取法,找出各树状柱杆件失稳时的屈曲荷载系数,求得对应屈曲荷载,并按欧拉公式反算计算长度系数。文献[3]以一多级分支树状柱为例,推导了有侧移情况下的树干计算长度系数的解析表达式,并通过有限元法验证了其合理性,并表示多级分叉树状柱的分支计算长度系数需通过线性特征值屈曲分析来反推。
本文以某树状结构工程设计为例,从整体结构弹性屈曲稳定分析出发,结合欧拉公式确定曲线型树状柱的计算长度,然后讨论了分支矢高比、分支与主干长度比、分支与主干线刚度比对分支计算长度系数影响,最后对树状结构进行了非线性分析。
1 工程概况
该工程塔楼形状趋于五边形,39层,结构高度179.97 m,底部三层带有外扩附属裙房,塔楼东北面有3层附属裙楼,与塔楼上部结构完全脱开,塔楼幕墙自标高57.7 m开始由主塔楼自由延伸至裙楼上方,形成屋面结构,屋面结构为空腹桁架体系,为了支承该屋面,在屋面覆盖范围内设置树状柱,如图6所示,一级分支为曲线,总计20棵树状柱,主干截面有P500 mm×20 mm、P550 mm×20 mm、P650 mm×30 mm三种,长度为3 m至17.7 m,一级分支截面有P300 mm×20 mm、P350 mm×20 mm、P350 mm×25 mm、P370 mm×20 mm四种,曲线长度为6m至21m,材料为Q345钢材,一级分支顶部与屋面钢结构采用刚接。图7为该工程典型树状柱造型。
2 计算长度系数确定
2.1 单棵柱计算长度系数
树状柱分支与主干采用铸钢节点,为刚性连接,以Tree-Z02树状柱为例,考虑分支上部悬臂、铰接、刚接三种约束情况,对各个分支施加一对集中力进行线弹性屈曲分析,然后反推计算长度系数,如表1所示,悬臂时计算长度系数接近3.0,铰接时为1.0左右,刚接时为0.7左右。因此分支上部与主结构采用刚接更有利,除了能减小分支的计算长度,还可以增加树状柱的刚度。

图6 树状柱分布Fig.6 Distribution of dendritic column

图7 典型树状柱造型Fig7 Modeling of dendritic column
表1不同顶部约束时分支的计算长度系数
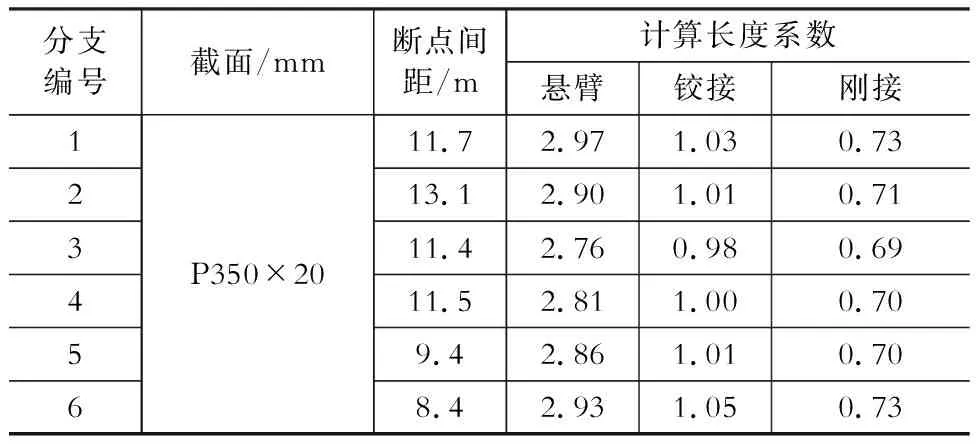
Table 1 Effective length coefficients of deferent constraint dendritic column
2.2 整体分析方法
为了考虑与树状柱分支相连的杆件初始内力和约束影响,宜将树状柱放入整体模型中分析,来计算其分支计算长度系数。目前的工程实践中,对于复杂空间杆系结构计算长度系数的确定主要分3个步骤:①对主导荷载作用下的整体结构进行静力线性分析得到所分析杆件的轴力作为初始态轴力;②对主导荷载作用下的整体结构进行线性屈曲分析,得到所分析构件对应的临界荷载系数;③用所分析构件对应的临界荷载系数乘以其初始态轴力,得到屈曲荷载,然后根据欧拉公式反算该构件计算长度系数[2]:
(1)
但是上述方法要在众多失稳模态中识别出某根杆件对应的失稳模态,工作量是巨大的,需要做些改进。由于,结构的屈曲模态与荷载大小无关,而临界荷载为临界荷载系数与初始荷载的乘积,并且本工程案例中,树状柱主要受轴向力作用,那么,可以在要分析的杆件上加一对较大的集中力,该构件的屈曲临界荷载系数就会变小,相应的屈曲模态就会最先得到,可以想到,如果一对集中力足够大,前几阶屈曲模态中就能找到该构件的屈曲模态。经多次试算,虚拟集中力为主导荷载作用下分支最大轴力的10倍的数量级时,前几阶屈曲模态中就能找出分支对应的屈曲模态。事实上,虚拟集中力大小取该构件两端简支约束下的欧拉临界荷载值是最有效的,计算长度可取约束点间的直线距离,此时其临界荷载系数为个位数量级,本工程中分支最大轴力为193.3 kN,对应欧拉临界荷载为1 833 kN,因此本工程虚拟临界荷载取10倍最大轴力是合适的,当用在其他工程上时,建议虚拟集中荷载大小取对应的欧拉临界荷载值。
为了验证本文方法的适用性,取一两层平面框架,层高3 m,开间6 m,柱底固接,梁柱截面为H300×150×6.5×9,约束楼层水平位移,计算其一层边柱和中柱的计算长度系数,分别为0.662和0.648,规范值分别为0.706和0.685,计算值与规范值相差5%,说明本文方法的合理性。另外,本文方法是基于弹性稳定理论求得的屈曲临界荷载,不适用于有侧移框架。
2.3 整体分析结果
构件的屈曲模态是局部杆件基于外荷载作用及周边约束条件下发生的失稳,找出所分析构件的屈曲失稳模态是确定计算长度系数的前提。根据本文提出的分析方法,选取恒载和活载标准组合作为主导荷载,并在分析构件上施加一对集中力,由于“恒载+活载”作用下,分支最大轴力为193.3 kN,因此集中力大小可取103数量级,本文取1 000 kN进行线性屈曲分析。
以Tree-Z02树状柱为例,图8为分支编号,图9为其前三阶屈曲模态。第1阶模态为支点有侧移的曲线平面外弯扭屈曲,第2阶模态为支点无侧移的曲线平面外弯扭屈曲,第3阶模态为曲线平面内弯曲屈曲。由于屋面空腹桁架对各个支点约束强弱不同,前两种屈曲模态先后顺序也不同。分支主要发生曲线平面外的弯扭屈曲。

图8 Tree-Z02分支编号Fig.8 Branching numbering of Tree-Z02
Tree-Z02树状柱的6根一级分支的屈曲临界荷载、几何长度和计算长度系数见表2,同时也采用整体模型提取法[3]计算了Tree-Z02各分支的计算长度系数,并列于表2中,两种方法所得分支临界荷载相差5%左右,而计算长度系数相差只有0.02%左右,说明本文方法是可行的。Tree-Z02分支计算长度系数为0.7左右,非常接近单棵树状柱独立分析时刚接情况。

图9 Tree-Z02分支屈曲模态Fig.9 Buckling modes of Branching Tree-Z02
表2Tree-Z02分叉计算长度系数
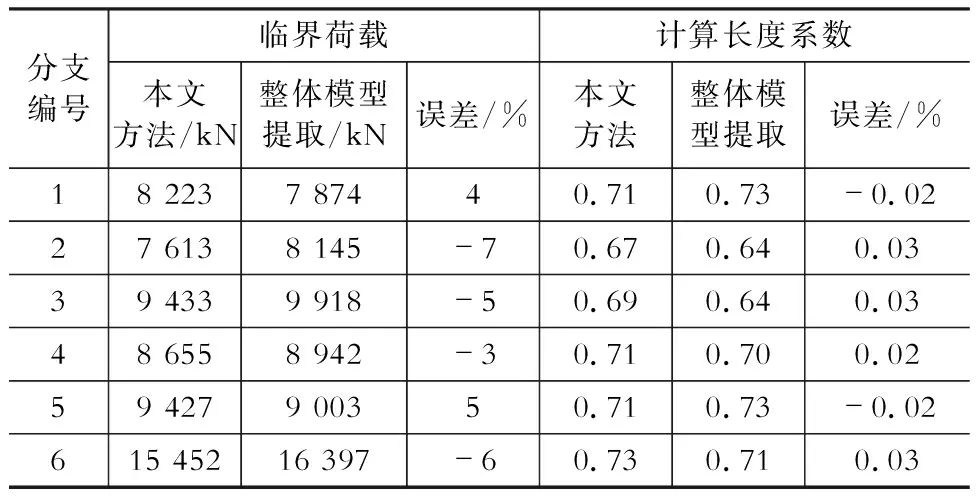
Table 2 Effective length coefficients of Tree-Z02
为了了解虚拟集中力大小对计算结果的影响,本文又取了100 kN集中力和1 000 kN集中力结果对比,以Tree-Z02树状柱为例,结果见表3,可以看出两种大小的虚拟集中力计算的临界荷载十分接近,误差在0.5%以内,由此计算的计算长度系数基本相同。但是,1 000 kN集中力作用下的分支屈曲模态均出现在第1阶,而100 kN集中力作用下的分支屈曲模态出现在第6~16阶,其中在前100阶屈曲模态内没有找到6号分支的屈曲模态。可见,“足够大的虚拟集中力”有助于快速甄别分支屈曲模态,而不影响分支临界荷载大小。
用本文方法计算了20棵树状柱的146根一级分支计算长度系数见图10,由图可以看出,树状柱一级分支的计算长度系数为0.6~0.8,与等截面无铰拱的计算长度系数很接近[4]。图11为分支计算长度系数和相同截面的一级分支初弯曲幅值v与分支端点距离L比值的关系图,由图可以看出,计算长度系数随v/L比值总体呈增大趋势,由于树状柱结构几何造型所限,v/L比值在0.05~0.25之间。图12为分支计算长度系数与分支弧长比关系,图13为分支计算长度系数与分支主干线刚度之比关系,规律不明显。设计时分支计算长度系数可统一取0.8。
表3两种集中力对应的计算长度系数

Table 3 Effective length coefficients of two concentrated forces
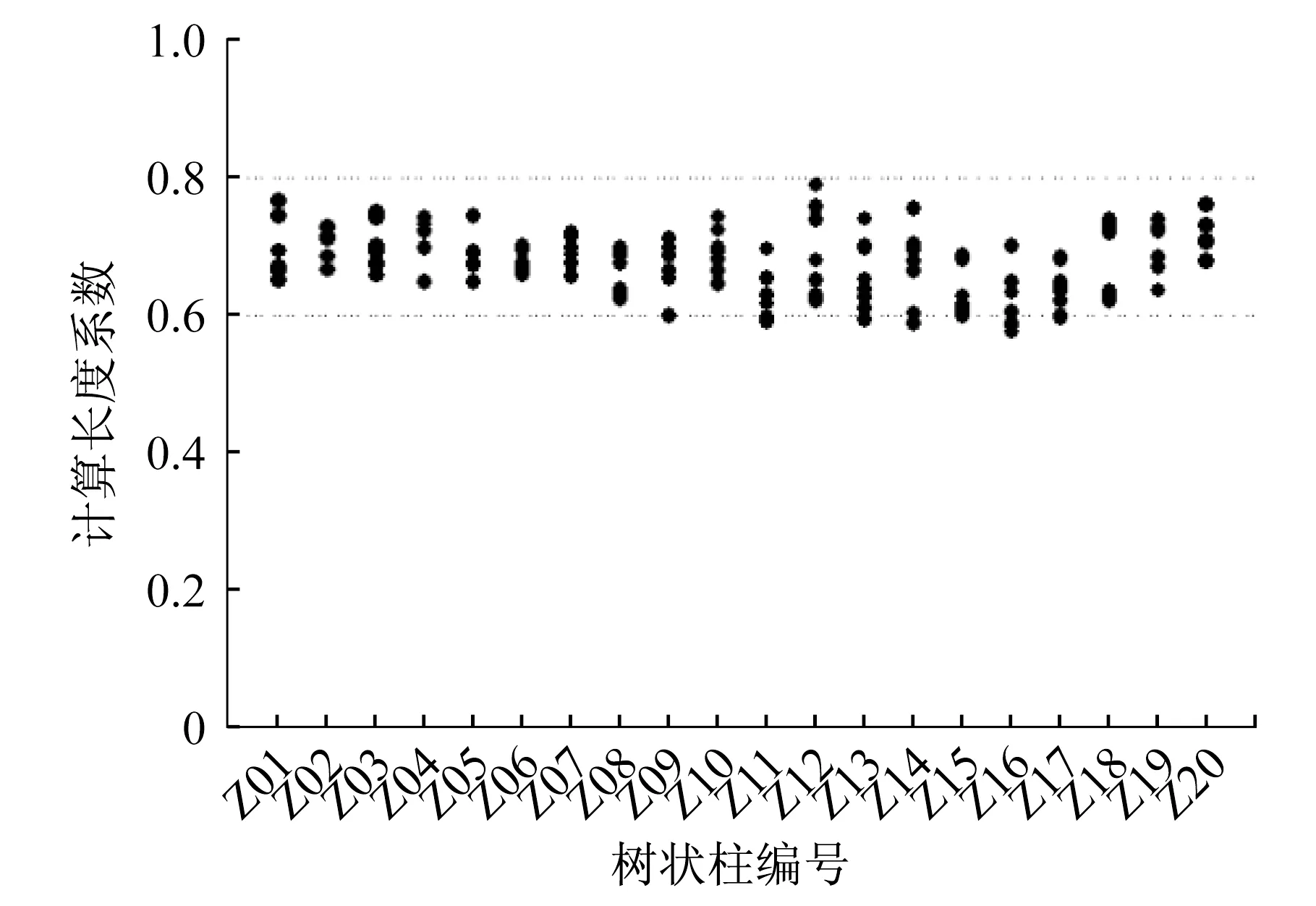
图10 树状柱一级分支计算长度系数Fig.10 Effective length coefficients of first branching structure members

图11 分支计算长度系数与v/L关系Fig.11 Relationship of effective length coefficients and v/L

图12 分支计算长度系数与分支弧长比关系Fig.12 Relationship of effective length coefficients and ratio arc length
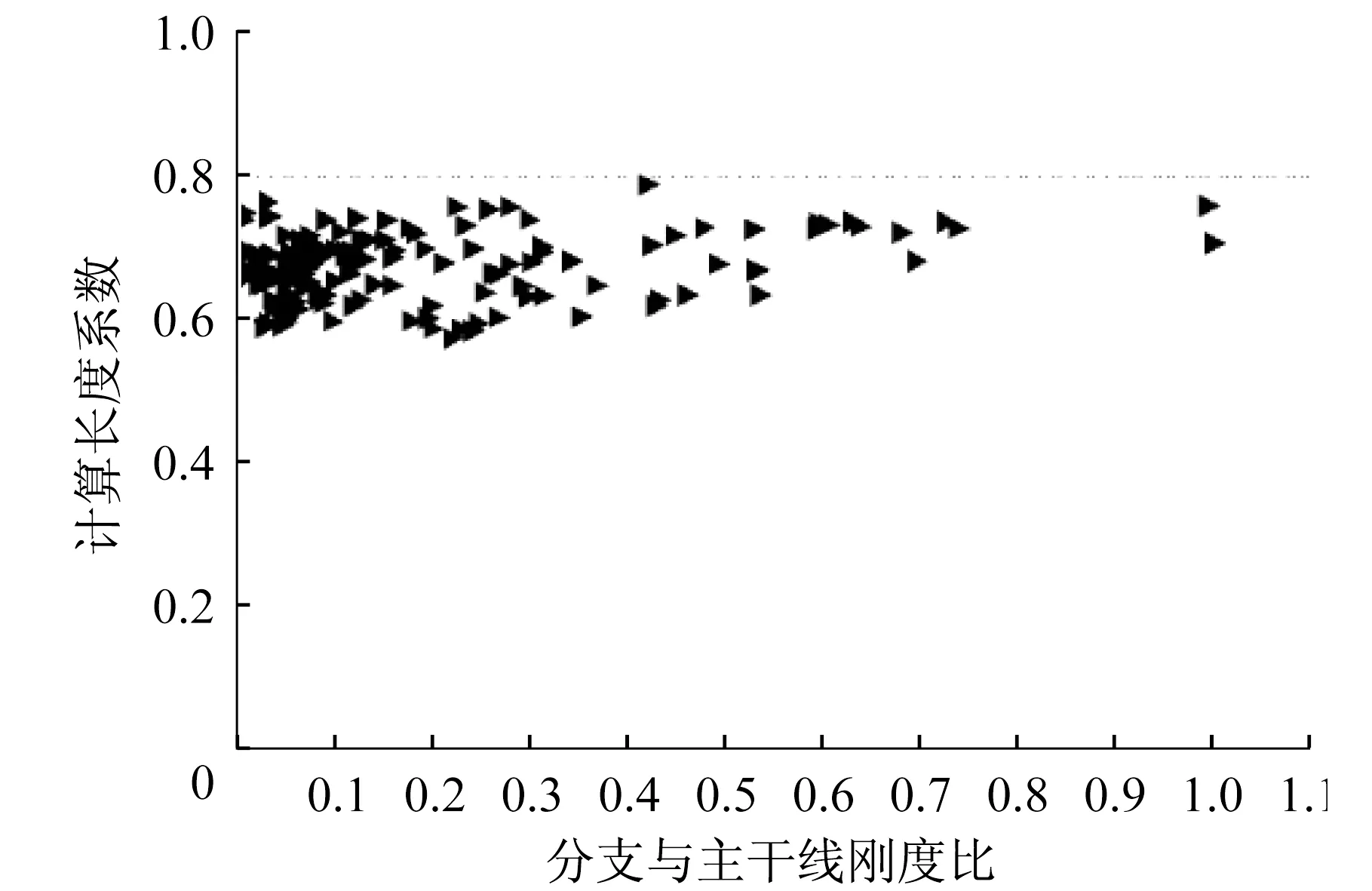
图13 分支计算长度系数与分支主干线刚度比关系Fig.13 Relationship of effective length coefficients and main ratio stiffness
3 非线性屈曲分析
取相应分支第1阶屈曲模态作为结构的初始几何缺陷,缺陷最大值为最长分支的1/300,同时考虑材料非线性,进行结构非线性分析。以Tree-Z02树状柱为例,其非线性分析结果如图14所示,结构失稳形式与线性屈曲分析的屈曲模态不同,是由于分支在曲线平面内弯曲失稳导致,分支沿着弯曲方向变形不断增大,该分支初始轴力100 kN,临界荷载对应的分支轴力为1 100 kN,因此荷载系数为11,大于规范[6]规定的2.0,满足稳定性要求。
4 结 论
通过对一树状结构工程实例中曲线形树状柱计算长度及稳定性研究,得出以下主要结论:

图14 考虑双重非线性的稳定分析结果Fig.14 Stability analysis with geometric and material nonlinearity
(1) 在整体模型提取法基础上,在分析构件上施加一对“足够大的集中荷载”,可以快速获得该构件屈曲模态,从而计算构件计算长度系数,与整体模型提取法计算结果误差在0.02%左右,本文方法合理可行。
(2) 分支顶部约束方式对分支计算长度系数影响较大,分支顶部宜采用刚性连接;随着矢高比v/L增大,分支计算长度系数有增大趋势;分支与主干长度比和分支与主干线刚度比对分支计算长度系数无明显影响。
(3) 对于本文所分析的曲线型树状柱,当分支顶部采用刚接连接时,分支计算长度系数在0.6~0.8之间,设计时可统一取0.8。
(4) 曲线型树状柱结构的的安全系数达到11,大于规范[6]规定的2.0,满足稳定性要求。
——超集中力
—— 梁在集中力作用点处的剪力分析

