基于Elman神经网络预测的机动目标跟踪滤波算法
郭剑鹰,夏李玮,刘华军
(1.华域汽车系统股份有限公司,上海 200041;2.南京理工大学计算机学院,江苏 南京 210014)
0 引言
随着航天探测、智能汽车、安防监控等系统的发展,实时准确地获取目标运动信息显得愈发重要。一方面,目标的大范围、高机动使得探测跟踪系统的动态性和非线性特征增强;另一方面,测量手段的多样性也会导致传感器误差特性异常复杂[1]。这些探测跟踪系统面临的共同问题之一是需要提升快速机动目标跟踪的稳定性和精度,其核心是运动建模的不确定引起的状态优化估计问题,也就是常见的滤波问题。随着机动目标跟踪技术研究的不断深入,涌现了很多实用的滤波算法,如卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)和粒子滤波(PF)等[2]。这些基本的滤波算法结合时下较为成熟的机动目标运动模型[3]可以较好地实现对机动目标的跟踪。但随着目标机动性不断提高,机动目标跟踪的对抗环境也日趋复杂,常规的机动目标模型,如Singer模型[4]、Jerk模型[5],在跟踪强机动目标时,难以适应复杂多样的机动形式;常规的滤波算法,比如IMM等[6],难以适应时变的机动形式。因此研究者不仅应从运动模型入手,构建能适应强机动形式的运动模型,还需要对滤波算法进行优化调整,使得滤波算法能够适应不同的机动场景。
目前,常见的机动目标跟踪滤波方法主要分为三种类型。一是对滤波器的机动参数进行自适应调整,即根据某种动态调整策略引入加权因子的方式,对机动参数进行自适应调整,如Singer模型、Jerk模型、当前统计模型等[7]。二是利用神经网络或者回归的方法对目标的状态估计进行预测,并可进一步通过神经网络训练学习机动参数,从而预测出当前时刻的最优状态估值来更新目标的估计[8-9]。三是结合以上两种方式既对滤波参数进行自适应调整,同时也对状态估计进行优化更新,如NEKF[10]、ELM_UKF[11]等滤波算法。这三种类型的优化方法都是在单次滤波结束之后进行方差或者估计值的调整,其优化过程相对于滤波有一定的滞后,仍旧会有一定的滞后误差。
本文提出的基于Elman神经网络预测的机动目标跟踪滤波算法,是一种紧耦合跟踪滤波器。它将优化估计过程提前至滤波的预测阶段,使得目标在跟踪预测阶段就有一个相对优化的预测值和调整后的噪声方差,从而就减少了优化过程滞后所带来的误差。
1 基于神经网络预测的UKF紧耦合滤波器
以雷达跟踪机动目标为例,将雷达位置设为坐标原点,定义k时刻机动目标状态向量为Xk=[x,y,z,vx,vy,vz,ax,ay,az]T,量测向量为Zk=[r,a,e]T,其中x,、vx,、axy,、vy,、ay和z,、vz,、az分别表示直角坐标系下目标在x,y,z坐标轴方向上的位置速度和加速度分量;r,、a,、e分别表示极坐标系下目标的距离、方位和俯仰角。基于此,可建立目标的跟踪系统模型:
(1)
式中,f(·)为目标状态转移函数,h(·)为传感器观测函数,λ(·)为未知时变的目标机动项。一般而言,假设ωk和vk为服从高斯白噪声分布的随机变量,即P(ωk)~N(0,Qk),P(vk)~N(0,Rk),Qk和Rk代表过程噪声协方差矩阵和测量噪声协方差矩阵。
解决该系统模型的常规滤波算法有:EKF、UKF、CKF和PF等,UKF即无迹卡尔曼滤波滤波精度和效率方面均具有优势,得到了大量应用。在预测阶段通过UT变换产生大量Sigma点进行预测加权并逼近真实预测结果,其状态向量和状态协方差矩阵的预测如式(2)、式(3)所示:
(2)
(3)
式中,χi表示UT变换后的Sigma点。由UT变换的理论分析和实验可知,变换后所产生的Sigma点近似服从高斯分布,经过f(·)变换后仍能较好地逼近高斯分布。在机动目标跟踪情况下,前后时刻状态预测还有一个未知且时变的机动项λ(·),每个Sigma点均包含了机动项引起的误差,这种误差不会随着状态方程而变化。而最终的状态预测值是在Sigma点加权求和之后得到的,所以每个Sigma点所包含的机动误差项与最终预测值的机动误差项之间存在某种函数对应关系,可定义为:
Err(f(χi))=hi(λ(k))
(4)
而在神经网络预测的模型中:
[λ(k),α]=h(Zk-Xk|k-1)
(5)
所以,每个Sigma点的机动误差项求取公式可定义为:
(6)
理论上,Elman神经网络可以逼近任意的非线性函数[9],因而Γ(·)可以通过Elman神经网络进行拟合预测,即可获得每个Sigma点的机动误差项,从而更新状态预测值。
在滤波器设计中,如果对每一个Sigma点都进行机动误差项的函数拟合,会大大增加计算量,而且神经网络的函数拟合是一个非常耗时的过程,并不利于实时在线的跟踪滤波。由于Sigma点近似服从高斯分布,而且权值相近,可以假设每个Sigma点的相对机动误差近似等于状态预测值的相对机动误差,只需要做一次函数拟合即可,如式(7)所示。新型滤波器的结构框图如图1所示。
(7)

图1 基于神经网络预测的新型滤波器模型结构图
2 基于Elman神经网络预测的机动目标跟踪滤波算法
为了验证本文算法不受运动模型影响,假设目标运动遵照常加速度(CA)模型,即:
(8)
详细的基于Elman神经网络预测的跟踪滤波算法为:
1)对上一时刻的最优估计进行UT变换,获得一组Sigma点和相应权值。
(9)
(10)
2) 对于每个Sigma点进行状态值的一步预测。
(11)
3)对于预测后的Sigma点进行加权求和,获得初始状态预测值。
(12)
4)将观测值与初始状态预测值的差作为待测数据。
(13)
(14)
6)使用训练好的神经网络对当前时刻的测试数据进行测试,得到当前时刻的相对机动误差和过程噪声的尺度因子。
(15)
7)对于每个Sigma点,根据调整后的目标状态方程进行二次预测,得到最终状态预测值和协方差矩阵:
(16)
(17)
(18)
具体的滤波算法流程图如图2所示。
3 实验及结果分析
仿真实验设计了多种不同的机动形式,如双S形、螺旋形弯道对于每种机动形式不同的随机误差。针对每个运动情形分别使用IMMELM的优化估计模型[9]、ELMUKF优化模型[11]和本文提出的基于Elman神经网络预测的滤波器进行1000次Monte Carlo实验,对比模型下滤波器的跟踪滤波精度,从而定量基于Elman神经网络的紧耦合模型的优势。实验所采用的评价指标主要是收敛性、无偏性、滤波精度和效率。
3.1 收敛性与效率
场景中目标以v=200 m/s的恒定速度在空中设定好的双S形弯道飞行,期间目标最大机动加速度为amax=64 m/s2,属于较强机动场景,场景中模拟了Δr=300 m,Δa=0.5°,Δe=0.5°大小的高斯白噪声。图3为当前场景下IMMELM模型、ELMUKF模型和本文方法的滤波轨迹图和单次滤波误差分布,其统计结果见表1。

表1 误差均值和均方根值统计结果
由图3和表1可得,这三种运动模型均可以实现快速收敛,一般在20~50个数据左右达到基本稳定收敛。对三种滤波模型进行比较,本文算法拥有最好的收敛速度与滤波性能。同时在效率方面,相比ELMUKF算法也有一定程度的提升。
3.2 机动形式的适应性
场景一中目标以v=200 m/s的恒定速度在空中以设定好的双S形弯道飞行,期间目标最大的机动加速度为amax=16 m/s2,属于弱机动场景;场景二中目标以初速度v0=300 m/s的恒定速度在空中以设定好的螺旋形弯道飞行,期间目标最大机动加速度为amax=90 m/s2,属于强机动场景。上述种场景均模拟了Δr=300 m,Δa=0.5°,Δe=0.5°大小的高斯白噪声。图4分别是两种机动情形下IMMELM模型、ELMUKF模型和本文的滤波轨迹图;图5是两种机动情形1000次Monte Carlo仿真的位置误差均值和均方根值的分布图,统计计算结果如表2所示。

图2 基于Elman神经网络预测的跟踪滤波算法流程图

模型场景一场景二位置误差均值/m位置误差均方根/m位置误差均值/m位置误差均方根/m测量值312.0497167.7742302.6656165.0034IMM-ELM模型251.1366135.2978238.9548130.2163ELM-UKF模型210.6755105.6455207.7997104.8658本文方法161.919385.5402168.992686.2870

图3 滤波轨迹与误差分布图

图4 两种不同机动场景下的滤波轨迹图
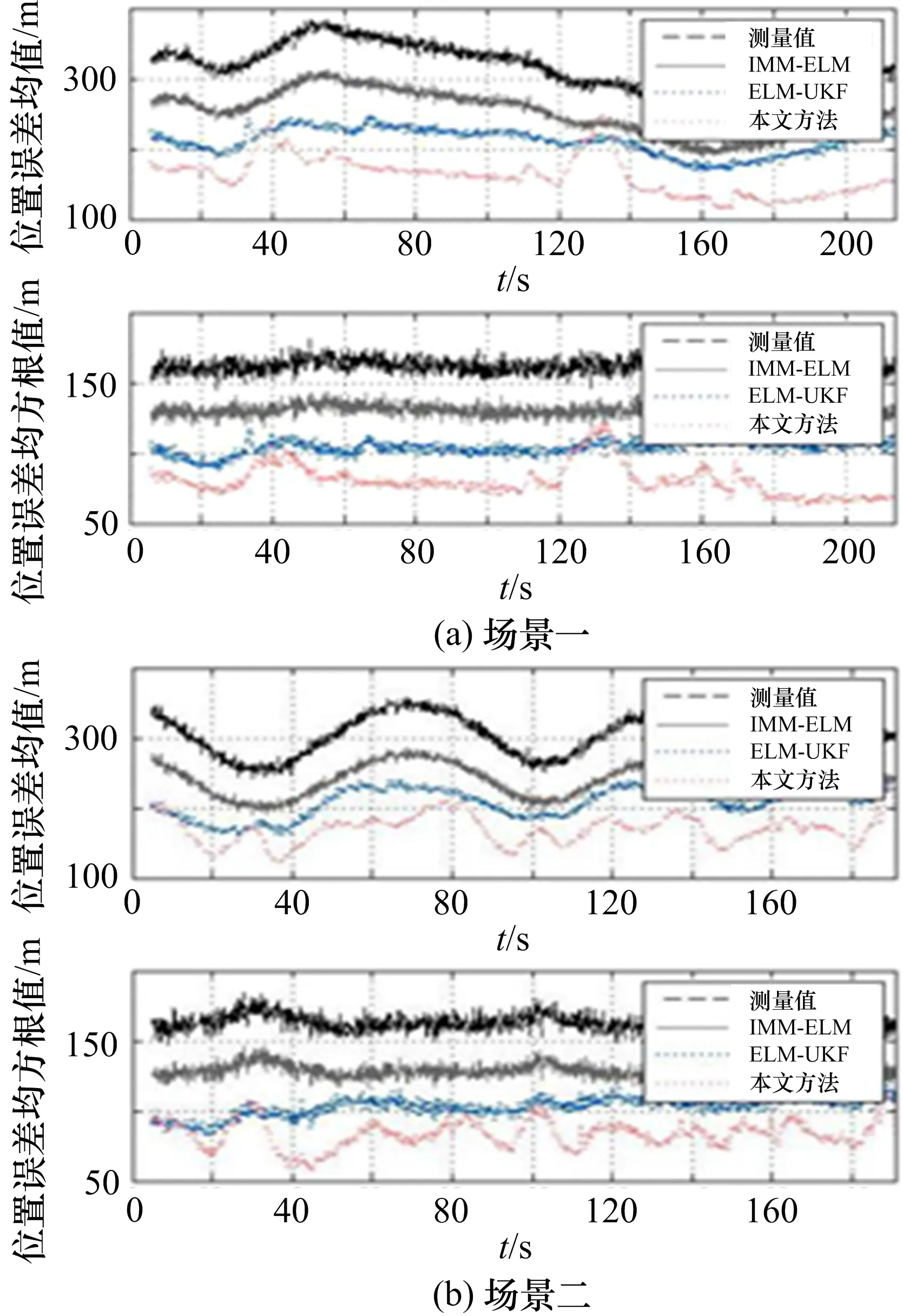
图5 两种机动情形下1000次Monte Carlo仿真均值和均方根值分布图

图6 两种随机误差下1000次Monte Carlo仿真误差均值与均方根分布图
由图5和表2得,本提出的紧耦合模型与ELMUKF模型相比,在两种机动场景下,其滤波误差均值分别降低了23.14%、18.68%,滤波误差均方根值分别降低了19.03%、17.72%。可以看出,本文法在场景下均有着相对不错的跟踪性能。
3.3 随机误差的适应性
针对场景一中的目标机动形式,Δr=500 m,Δa=1.0°,Δe=1.0°和Δr=50 m,Δa=0.2°,Δe=0.2°。图6为两种随机误差情形下的位置误差均值和均方根值的分布图,其统计结果如表3所示。
由图6和表3可得,在较高随机误差大小下,本文方法优于IMMELM模型与ELMUKF模型的滤波精度,表现出了良好的滤波性能。
但在较低的随机误差情况下,本文法稍微弱于方法,这是本文方法在计算相对机动误差时假设了当前目标状态方程是最优的,而这种假设本身就存在着一定的误差。当目标随机误差接近于模型假设的误差量级时,这种误差无法被忽略。

表3 两种随机误差下1000次Monte Carlo仿真误差均值与均方根统计表
4 结束语
随着空间探测、智能汽车、安防监控等领域对机动目标的跟踪要求不断提升,机动目标的跟踪滤波算法也在不断完善。从机动模型构建到自适应滤波器的设计,应充分考虑构建能适应强机动场景的运动模型,同时还需要对滤波算法进行优化调整,使其能够适应强弱不同的机动场景。本文从模型和滤波算法两个角度设计了一种基于Elman神经网络预测的新型跟踪滤波方法,具有较好的机动适应能力,特别可提高强机动目标跟踪滤波器的性能。■

