基于人工场模型的无人机侦察线路规划
孙瑞祺,周玉宁,高志勇,颜楚雄,高 路
(1.北京航天长征飞行器研究所,北京 100076; 2.空军驻航天一院军事代表办公室,北京 100076)
0 引言
无人飞行器的种类很多,在战争中的应用也不同,因此对各种不同应用的无人飞行器进行航迹规划是有区别的。侦察无人机为了收集目标信息,首先需要保护无人机本身,避免遭受损伤。在侦察航迹规划时,侦察无人机应该针对其行动特点避开所有的威胁,尽量避免让无人机出现在敌方的雷达监控范围内以及地形高峰。但是,如果任务目标非常有价值,必须侦测或者消灭,然而这类目标往往会被保护得尤为严密,则需要无人飞行器尽可能覆盖多的需侦察区域才能完成任务。前一种是考虑航迹的安全性而进行研究的航迹规划,为战术级航迹规划;后一种是主要考虑的是任务的绝对性而研究的航迹规划,为战略级航迹规划[1]。
无人机任务的分配和线路规划问题通常被简化为以下两种典型模型:一是车辆路径问题模型。该模型是乘客乘车问题的延伸,通过将无人机看作车辆,任务目标比作乘客目的地,将无人机任务分配问题映射到车辆路径问题[2]。二是多旅行商问题模型。该摸型将单一无人机看作一个旅行商,这样多无人机的任务分配问题就可比作多旅行商问题,尤其适用于带有时间限制的任务规划[3]。
然而,上述两种模型的建立都需要在整个侦察地形中选取到合适的重要任务节点,然后再将上述重要节点转化为车辆路径问题或者多商旅问题模型[4]。在实际作战中,往往不存在这样的任务节点,那么任务节点应该如何选择和确定是值得关注和研究的问题。本文提出了一种同时考虑侦察覆盖率以及雷达威胁的重要节点选择方法。该方法同时考虑了地形、无人机飞行能力以及雷达辐射源的威胁,将线路规划问题转化为上述两种模型,可以实现实际地形的侦察线路规划,具有很好的实用价值。
1 模型的建立
1.1 侦察任务模型
一幅典型的山区高程图如图1所示。是以1 km ×1 km为单元在地面绘制网格,再以每个单元格平均的高程数据制成矩阵绘制的图像。无人机的任务是在尽可能躲开雷达和山峰的情况下对整个区域内的低于3500 m的区域进行侦察,发现并寻找敌方目标。在没有任何先验知识的情况下需要规划出一条侦察路线,对整个区域进行侦察,使得无人机尽可能躲开高耸的山峰侦察更多的区域。图1中的垂直坐标为地形的高程数值(m),横纵坐标为地面的网格单元数量,网格单元大小为1 km2,下同。

图1 某山区高程地形图
在规划无人机路线的同时需要考虑到无人机的最大拐弯角[5],它限制了生成航迹的转弯范围,即转弯必须在小于或者等于事先确定的最大角度之内;最大爬升俯冲角,它约束了在垂直平面内,航线上升和下滑最大的角度,取决于无人机自身的机动性能;最小航迹段长度,它表示无人机在还没有改变飞行姿势之前所必须持续直线飞行的最小距离,为了减少导航误差,在无人机的惯性制导系统中,远距离飞行时一般避免迂回行进和频繁转弯[6];最低飞行高度,为了尽量防止在通过敌方防御区时,被探测器发现或是被地面防御装置摧毁,无人机在飞行时高度应该尽可能低些,但是又不能太低,飞得过低又会加大与地面相撞的概率,应使无人机距离地面的高度在某个特定值的范围内,尽量减小飞行高度。
1.2 视场模型
以图1山区中的重点区域为例,对该区域内每个3500 m以下的网格结点做如下分析:
首先,假设无人机飞行高度恒为4200 m,根据视线可逆的原理,将在地面某点看无人机的仰角大于60°且视线不被山体阻隔视为该点被巡查。那么对于地面上的某网格点,以这点作为顶点,垂直于海平面的直线为轴线,夹角30°为母线做出一个圆锥,则这个圆锥与该点上空位于4200 m平面相交,得到的圆形区域内的各点都可以观察到地面上的该点。

图2 地面某点观察圆锥示意图
其次分析图2中各点。对于图2中给出的1、2、3、4、5点,假设这5个点都在3500 m以下,均是需要侦察的点。分别按照之前的方法对4个点做出圆锥体,那么在4200 m的平面的各圆锥地面将会形成重叠。图2中蓝色区域意为无人机在此区域内可以同时观察这4个点,红点区域意为无人机在此区域内可以同时观察这3个点,黄色区域意为无人机在此区域内可以同时观察这2个点,绿色区域意为无人机在此区域内可以观察这1个点。
以实际地形中某个点为例进行视场分析,以此点为中心及其相邻的8个点分别按照前述方法做圆锥,并在4200 m高度平面内形成投影。这9个点也会形成4个正方形单元格。每个单元格大小即为前文中给出的单元格大小。
在4200 m高度做出此中心点的投影,并以该点为圆心,以5个单元格为半径做出一个圆,这些点将会形成一个集合S。初始时将每个点设为n=0,n为记数所用。若地面上的点向天空做圆锥,那么在这个圆锥底面将会覆盖集合S中的一部分点。这些被覆盖了的点都进行n=n+1的操作。
图1区域中的其他点用同样的方法进行投影,当投影圆与单元格相交,n=n+1;以此类推,即可得到如图3所示的区域结果。
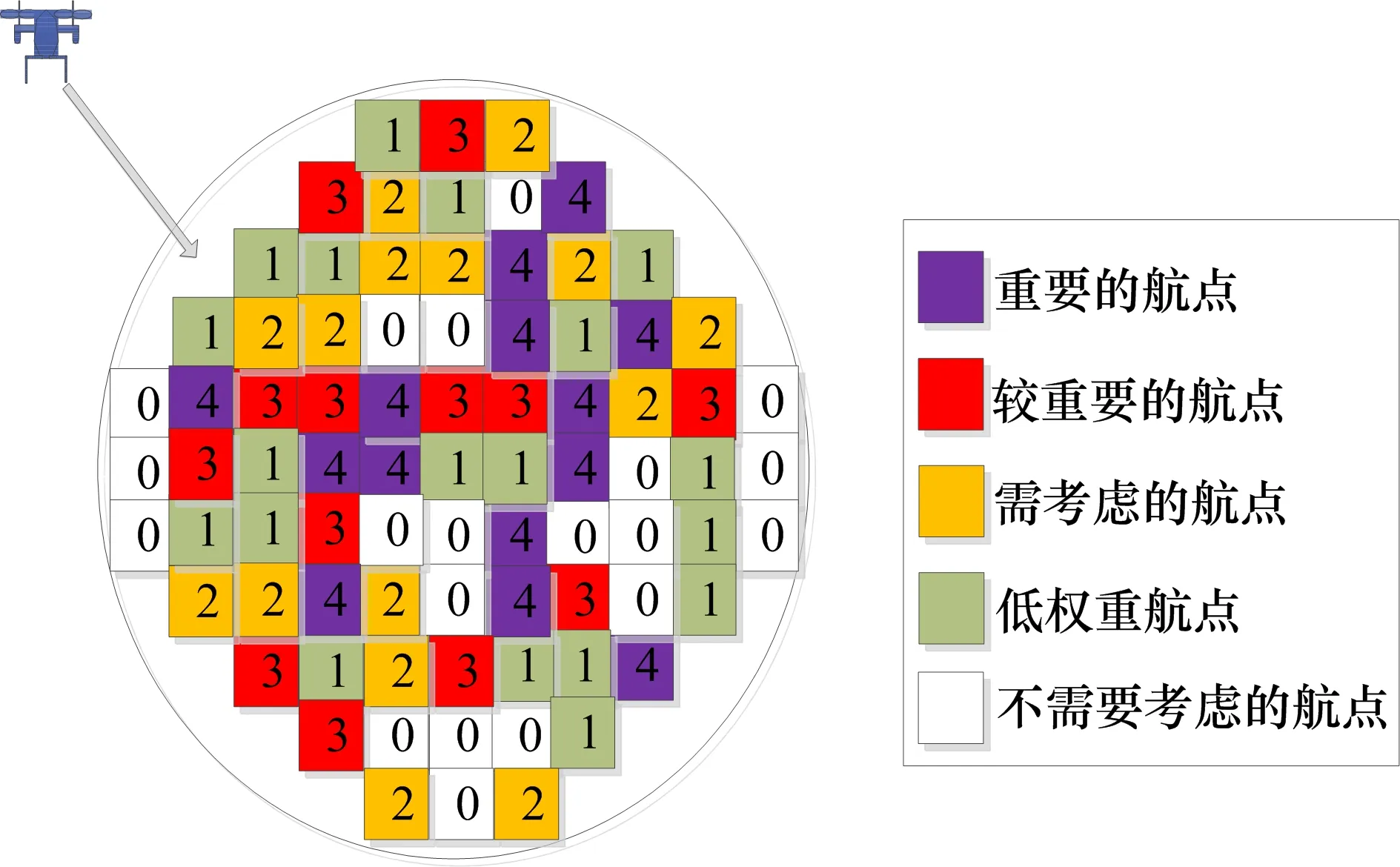
图3 图1区域各航点比较示意
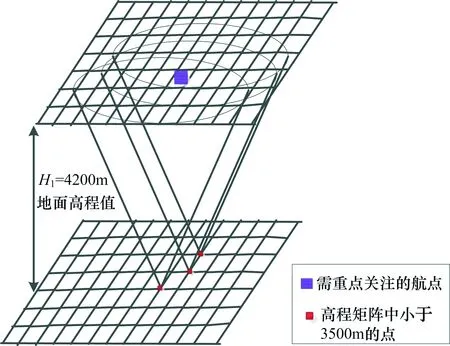
图4 需要重点关注的航点图示
如图4中所示,4200 m高度平面,紫色的位置有3个圆相交,即为图5中红色区域较重要的航路节点。将图1域中可以观测到较多3500 m以下位置的航点记录在另一个等大的对应矩阵中,即映射矩阵B,可以得到一个视场矩阵模型。在视场模型中还要相应地加入一些无人机航行限制条件的权值。
对于区域内海拔3500 m以下的点,从地面某点看无人机的仰角θ≥60°,且视线不被山体阻隔视为该点被巡查。
根据这些已知条件,通过算法映射得到了1个与图1中地形相关的映射矩阵图5,该矩阵中的数值表示的是映射矩阵中该点可以观测到的地面需观测点的数目。数值越大,该点的权值越高(红色为高权值区域),证明该航点的重要性越强。
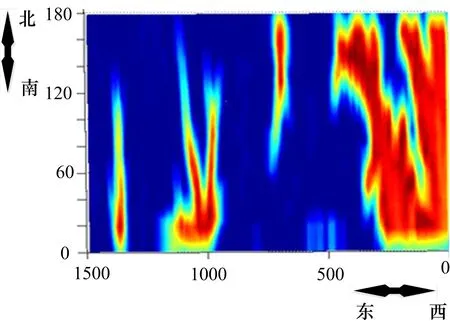
图5 人工视场矩阵图
1.3 威胁场模型
增加1个人工威胁场模型,进一步地缩小可航行的线路范围。人工势场法APF结合了物理中场的概念,场中的物体,受到来自目标的引力和来自障碍物的斥力,在合力的作用下运动。将山峰和已知雷达站视为危险点的中心,构造一个威胁势场,增加限制航路的条件。根据视场模型的计算结果得到一片可以观测到最多的点的区域,最优观测区域向外辐射,形成梯度,观测权值与势场类似。
势场威胁值随着无人机与障碍物的距离减小而增大,为防止距离为0时,威胁无限大的情况出现,设置最小安全距离d0,斥力表达式为:
Frep(XR)=
(1)
式中,Kr为威胁场常量,XR,X0分别表示无人机和障碍物位置,d(XR,X0)为一个矢量,其大小为无人机与障碍物之间的距离|XR-X0|,方向为障碍物位置指向无人机位置。当无人机与障碍物的距离大于dm时,无人机不再受场的影响。
无人机在执行任务时,一方面利用地形躲避敌方的雷达探测或火力袭击,另一方面也需要考虑地形所带来的限制。根据对无人机飞行高度的假设,无人机很难飞跃4200 m以上的高峰,这增加了无人机撞地损毁的风险。已知地形威胁的模型的计算公式如下:
(2)
式中,U表示山峰造成的威胁总和,m表示该航迹点区域内山峰个数,Uj表示第j个山峰的威胁,peakj为第j个山峰的山顶高度,(x,y,z)表示无人机的地理坐标与高程数据,(hxj,hyj,hzj)表示第j个山峰的位置坐标,hrxj,hryj分别表示第j个山峰在(hrxj,hryj)处的梯度方向,hrzj为第j个山峰的高程。
在本次建模中,如图6所示,同时考虑视场和威胁场的权值,分别对视场值和威胁值增加一定的权值。视场值是该航点可观测到的地面观测点数量乘以τ视,威胁值是定义的该航点与周围陡峭山峰的人工势场值。那么映射矩阵B中每一个元素的权值值变为:
Ui,j=τ视Ai,j-U威胁
(3)
通过选取每一个区域地形内总场值最优的点,可以得到一些权值最优的节点,这些节点是侦察需要经过的重点区域。将这些点一一列出,就可以将侦察问题转化成为一个多重要节点的多商旅模型。
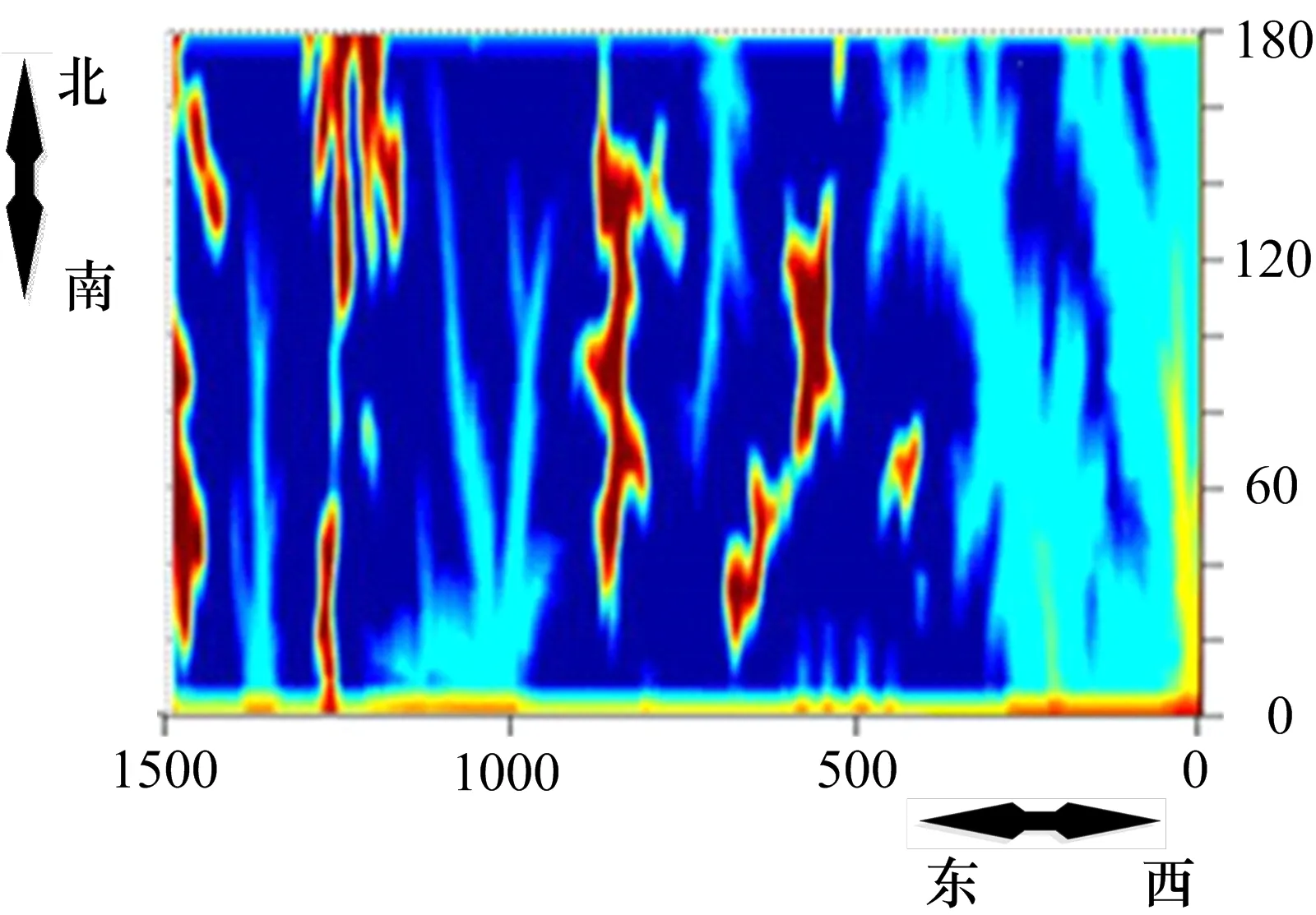
图6 人工威胁场图
2 线路规划
在视场模型和威胁场规划的基础上将无人机线路规划转化为多旅行商问题。本次仿真中一架无人机从靠近地形边缘的节点出发,巡查图1地形中人工场模型中的重要节点,最后航行出图1范围。因此,路线规划模型可以描述为:
建立一个赋权无向完全图G=(C,X,D),其中目标群集合C={c1,c2,…,cn},它包含出发点H(定义为c1)以及需要巡查的集合{c2,…,cn};边集合X={xij|i,j=0,1,2,…,n},其中xij为目标群ci到目标群cj的边,表示该条飞行线路是否应该执行;距离集合D={dij|i,j=0,1,2,…,n},表示目标群ci到目标群cj的距离。
单架无人机须从c1点出发,首先飞向目标群ci,沿一条路径侦查并且从目标群cj(ci≠cj)离开。每架无人机都至少到达一个目标群,任一目标群都需要被一架无人机侦查且仅被侦查一次。求路径长度,使得单架无人机的路径总和S最小。
令s1为无人机飞行的路线,求总路线S={s1},使目标函数值最小。即:
xii=0,j=1,2,…,m
(4)
式中,
(5)
3 模型求解及分析
根据上文所建立的模型,本文使用Matlab对无人机线路进行了仿真和规划。首先通过人工场模型,得到了一系列的权值峰值位置,选取了50个权值最高的节点。再使用多商旅问题的寻优方法,得到了单个无人机侦察图1中地形的最短最优航迹,如图7所示。
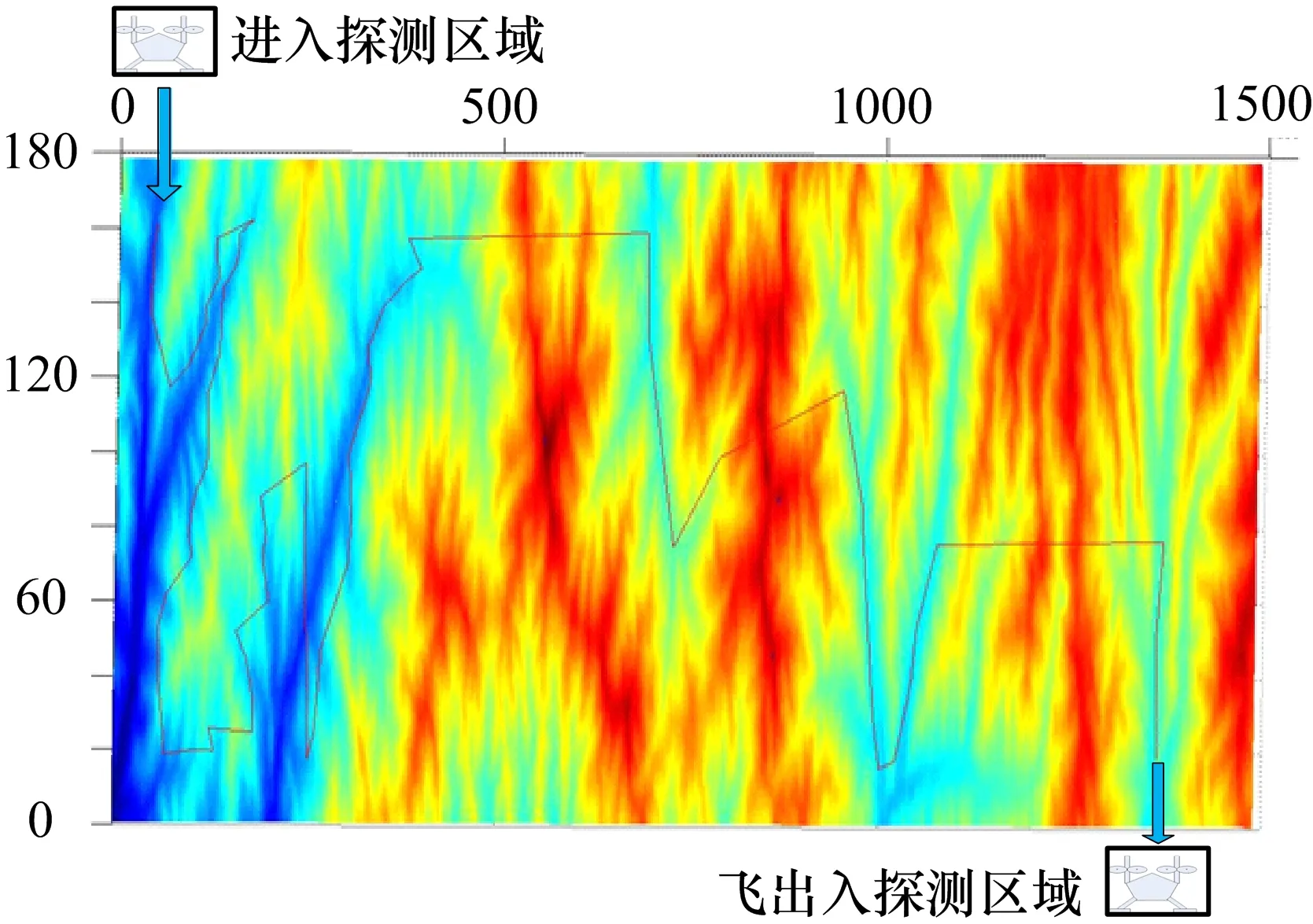
图7 无人机侦察线路规划仿真结果
通过文中模型规划出的线路模型是以最大覆盖率以及躲避地形高峰为标准制定任务节点的。这样制定出的线路可以在没有地方火力配备以及兵力部署的情况下制定无人机的侦察路线。选取的节点越多,线路规划更为合理和精确,但同时也会增加运算量。
4 结束语
本文对无人机在未知地形搜索区域内的侦察搜索线路规划问题进行了研究。 通过建立人工视场和威胁场的方法,利用地形图中的高程数据进行分析,提取节点,把无人机侦察搜索线路规划问题转化为了一个多旅行商问题。这种人工场建立方法可以有针对性地对地形进行分析,自适应性强,可以快速制定侦察搜索线路方案。这种人工场模型可以得到多个节点结果,以无人机的航程最短和覆盖点数目作为评估准则,从而得到最优的线路规划结果。在今后的研究中,还可以进一步使用蜂群算法、蚁群算法等仿生学算法代替多旅行商模型,对侦察线路进行更精确的规划,得到更细致、更优的侦察线路规划结果。■

