高考物理弹簧模型问题解题要点分析
耿玉盛
(扬州市邗江区教研室 江苏 杨州 225009)
以轻质弹簧为载体,设置复杂的物理情境,力的概念、物体的平衡、牛顿定律的应用及能的转化与守恒是高考命题的重点.试题突出了对运动和力以及功能关系等知识点的考查;突出了对学生分析、综合能力等的考查.弹簧问题涉及的物理知识点较广,有,平衡类问题、运动和力的关系、运动的合成与分解、圆周运动、简谐运动、功和能量、以及临界和突变等问题.下面就高考试题中关于弹簧的问题做一些分析.
1 单个物体与弹簧相连在竖直杆上滑动问题

A.弹力对小球先做正功后做负功
B.有两个时刻小球的加速度等于重力加速度
C.弹簧长度最短时,弹力对小球做功的功率为零
D.小球到达N点时的动能等于其在M,N两点的重力势能差
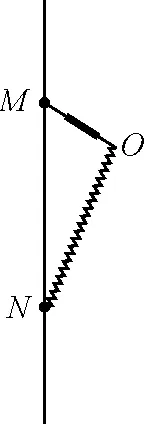
图1 例1题图
考点分析:本题中考查受力分析、牛顿第二定律的应用、瞬时功率的计算以及系统机械能守恒定律的应用.
解析:由题意可知在运动过程中受力如图2所示.小球的位移为MN,则从M→A,弹簧处于压缩态,则弹力做负功,从A→B弹簧从压缩变为原长,弹力做正功,从B→N弹簧从原长到伸长,弹力做负功,则选项A错.
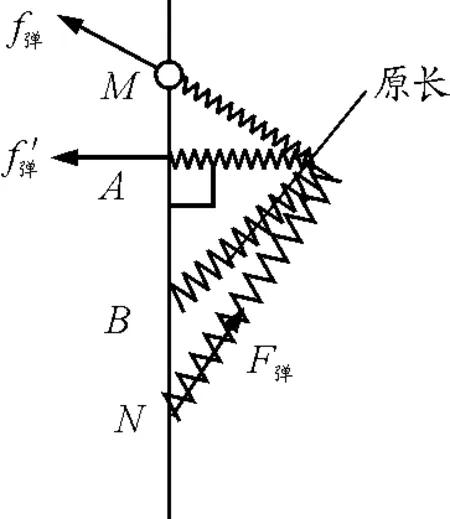
图2 运动过程分析
在A点受力如图3(a)所示,在B点弹簧处于原长则受力如图3(b)所示.F合=mg,则即a=g,选项B对.
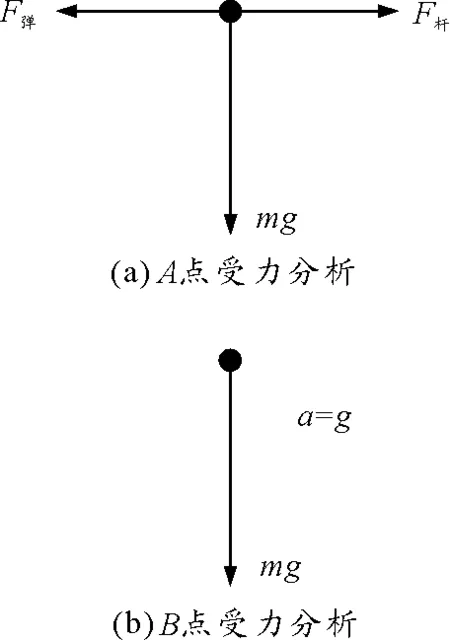
图3
在A点时,F弹垂直于杆,则P弹=F弹vcosα=0 ,选项C对.
从M到N小球与弹簧组成的系统机械能守恒,由于M,N两点弹簧弹力相同,由胡克定律可知,弹簧形变量相同,弹性势能相等,则选项D对.
点评:本题的分析思路与问题1基本相同,关键两个特殊位置,A处弹簧水平竖直方向只受重力,B处弹簧处于原长状态,物体只受重力.M,N两处弹力大小相等弹簧形变量相等从而确定M处弹簧压缩,N处弹簧伸长;其次是分析出M到N弹簧处于压缩状态且压缩量增大,从A到B压缩量减小,从B到N弹簧伸长.
【例2】(2015年高考江苏卷第9题)如图4所示,轻质弹簧一端固定,另一端与一质量为m,套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑.经过B处的速度最大.到达C处的速度为零.AC=h. 圆环在C处获得一竖直向上的速度v,恰好能回到A. 弹簧始终在弹性限度内,重力加速度为g. 则圆环()
A.下滑过程中,加速度一直减小

D.上滑经过B的速度大于下滑经过B的速度

图4 例2题图
解析:本题中考查受力分析、牛顿第二定律的应用、动能定理的应用以及功能关系.解答此题的关键:第一是特殊位置B处速度最大,学生要能理解从A到C过程中速度最大时,加速度为零,从而确定从A到B先加速,从B到C再减速;第二是向下和向上滑行时物体的受力情况分析,整个过程摩擦力都做负功;第三是从A到C和从C到A弹性势能的变化量相等.
弹簧的弹力是一种由形变而决定大小和方向的力.当题目中出现弹簧时,要注意弹力的大小与方向时刻要与当时的形变相对应.在题目中一般应从弹簧的形变分析入手,先确定弹簧原长位置,现长位置,找出形变量x与物体空间位置变化的几何关系,分析形变所对应的弹力大小、方向,以此来分析计算物体运动状态的可能变化.
2 弹性势能与动能相互转化的问题
【例3】(2016年高考全国课标Ⅱ卷第25题)轻质弹簧原长为2l,将弹簧竖直放置在地面上,在其顶端将一质量为5m的物体由静止释放,当弹簧被压缩到最短时,弹簧长度为l.现将该弹簧水平放置,一端固定在A点,另一端与物块P接触但不连接.AB是长度为5l的水平轨道,B端与半径l的光滑半圆轨道BCD相切,半圆的直径BD竖直,如图5所示,物块P与AB间的动摩擦因数μ=0.5.用外力推动物块P,将弹簧压缩至长度l,然后放开,P开始沿轨道运动,重力加速度大小为g.
(1)若P的质量为m,求P到达B点时的速度的大小,以及它离开圆轨道后落回到AB上的位置与B点之间的距离;
(2)若P能滑上圆轨道,且仍能沿圆轨道滑下,求P的质量的取值范围.

图5 例3题图
考点分析:本题考查了牛顿第二定律、功和功率计算、机械能守恒定律
解析:(1)地面上,Ep重转化为Ep弹,E机守恒
所以
|ΔEp重|=|ΔEp弹|
5mgl=Ep
此时弹簧长度为l
A→B过程能量守恒,有
Ep=EkB+Q
即
B→D过程动能定理,有
此后,物体做平抛运动
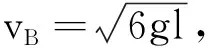
(2)假设物块质量为m′
则A→B过程能量守恒,有
解得
若要滑上圆弧,则
即
解得
若要滑上圆弧还能沿圆弧滑下,则最高不能超过C点.此时假设恰好到达C点,则根据能量守恒
Ep=Q′+EpC
5mgl=μm′g·4l+m′gl
解得
故若使物块不超过C点
综上
点评:本题是弄清两种情况下弹性势能的求解,答题主要出现问题:不认真审题,没有从题干中得到求解出弹簧弹性势能信息,导致从开始就落入在弹性势能求解的怪圈中.
在求弹簧的弹力做功时,因该变力为线性变化,可以先求平均力,再用功的定义进行计算,也可据动能定理和功能关系:能量转化和守恒定律求解.同时要注意弹力做功的特点
弹力的功等于弹性势能增量的负值.弹性势能的公式
高考不作定量要求,可作定性讨论.因此,在求弹力的功或弹性势能的改变时,一般以能量的转化与守恒的角度来求解.
3 外力作用下物体与弹簧连接问题

(1)弹簧的劲度系数;
(2)物块b的加速度;
(3)在物块a,b分离前外力大小随时间变化的关系式.

图6 例4题图
考点分析:本题考查了胡克定律、共点力作用下物体的平衡、牛顿第二定律的应用、匀变速直线运动规律的应用.
解析:(1)受力分析可得
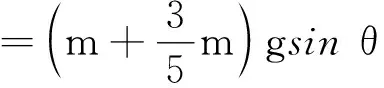
由胡克定律F=κx的弹簧的劲度系数
(2)设从开始运动到ab分离,经过时间t,位移x,有
对b,在2t时间内有
解得
可知ab分离时弹簧压缩量
对a,有
κΔx-mgsinθ=ma
解得
(3)对ab整体未分离前
其中
解得
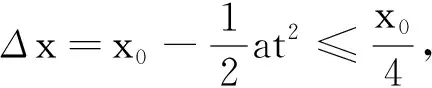
点评:本题的关键:第一是要理解a,b分离时a和b之间无相互作用力,且a仍有加速度,这样对a受力分析列出牛顿第二定律方程;第二是通过两段时间内的运动分析列出运动学公式,求出a,b刚分离时a,b通过的位移,从而确定此时弹簧的压缩量.
对于弹簧连接体的“动、静”结合问题的解答,关键是分析物体的受力特点及运动形式.对于匀加速直线运动,需确定运动的初、末状态所对应弹簧的形变量以及列出动力学方程,有时还需应用有关匀变速直线运动的公式,特别是两个物体刚要分离的条件是关键.
4 物体与轻杆和弹簧相连接问题
【例5】(2017年高考江苏卷第9题)如图7所示,3个小球A,B,C的质量均为m,球A与球B,球C间通过铰链用轻杆连接,杆长为L,球B,球C置于水平地面上,用一轻质弹簧连接,弹簧处于原长.现球A由静止释放下降到最低点,两轻杆间夹角α由60°变为120°,球A,球B,球C在同一竖直平面内运动,弹簧在弹性限度内,忽略一切摩擦,重力加速度为g.则此下降过程中()
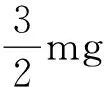
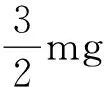
C.弹簧的弹性势能最大时,球A的加速度方向竖直向下
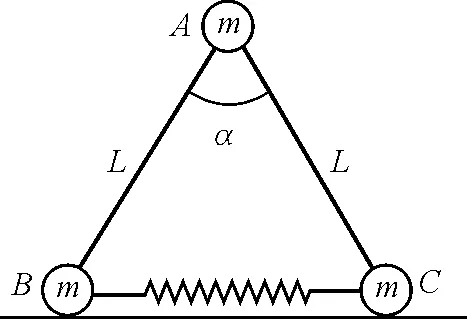
图7 例5题图
考点分析:本题考查了连接体问题中整体法和隔离法的应用、物体的受力分析、平衡问题、牛顿运动定律、机械能守恒定律等.
解析:球A的动能最大时,球A的加速度为零,竖直方向球A,球B,球C三者组成的系统处于平衡状态,由整体法可知球B,球C所受地面的支持力有:2N=3mg,因此选项B正确.
动能最大之前球A向下加速,有向下的加速度,对球A,球B,球C整体有:2N 球A越过动能最大位置后开始向下减速,弹簧继续伸长,当球A减速到速度为零时到达最低点,此时球A有向上的加速度,此时球B,球C速度也为零,弹簧伸长量最大,弹性势能最大,所以选项C错. 由系统机械能守恒定律可知球A减少的重力势能等于弹性势能的增加量.有 Ep=mgL(sin60°-sin30°) 所以选项D错. 点评:解决本题的关键是两个特殊位置,一是球A的动能最大时,球A处于平衡状态;二是球A在速度为零时,球A在最低点,球A,球B,球C速度为零. 【例6】(2015年高考江苏卷第14题)一转动装置如图8所示,4根轻杆OA,OC,AB和CB与两小球及一小环通过铰链连接,轻杆长均为l,球和环的质量均为m,O端固定在竖直的轻质转轴上.套在转 (1)弹簧的劲度系数κ; (2)AB杆中弹力为零时,装置转动的角速度ω0; 图8 例6题图 解析:本题以连接体杆、轻弹簧为模型考查了力的合成与分解、受力分析、共点力的平衡、牛顿运动定律,牛顿运动定律的应用、圆周运动及其应用、动能定理及其应用,知识点较多、综合性较强.第(1)问是连接体的平衡问题,采用整体-隔离法;第(2)问小环受的弹簧弹力与其重力平衡,小球则在重力和OA杆的弹力作用下在水平面内做匀速圆周运动;第(3)问外界对转动装置做的功,导致其他能转化为环增加的重力势能和小球增加的重力势能以及增加的动能,弹簧初态伸长的长度和末态缩短的长度相等,弹性势能相同,所以弹力做功为零. 总之,弹簧类问题综合性很强,物理情景复杂,物理过程较多,但只要我们仔细分析物理过程,准确地进行受力分析,确定物体或弹簧所处的特出位置(平衡位置、原长处、最大型变位置、物体和弹簧刚好分离出等)的条件,找出每一现象所对应的物理规律,正确判断各物理量之间的关系,此类问题一定会迎刃而解.我们在实际教学中可以结合相应的问题,采用微专题的形式组织复习、研讨,以提升学生解决弹簧问题的能力.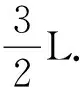

——《势能》

