“仿真物理实验”在物理问题研究中的应用
——以“寻找带电小球在复合场中的运动轨迹”为例
陈玺君
(丹阳市吕叔湘中学 江苏 丹阳 212300;广西师范大学教师教育学院 广西 桂林 541004)
1 问题场景
【问题】如图1所示,范围足够大的匀强磁场,磁感应强度为B,方向垂直纸面平面向里,同时在纸面平面内有一匀强电场,大小为E,方向水平向右.质量为m,电荷量为q的带正电小球从图中某一位置P出发,与水平方向成45°斜向右上方射入场区,小球所受电场力与其重力大小相等,试分析小球所有可能的运动轨迹.
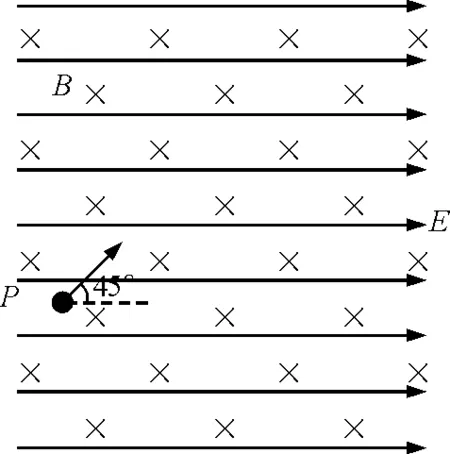
图1 题图
2 初步理论研究分析
首先从理论上简单分析:为了便于研究该问题,可以以带电小球出发点P为坐标原点,v0方向为x轴,建立如图2所示平面直角坐标系.
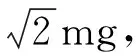
图2 建立有角坐标系
鉴于v0与v的大小关系不明确,这时显然有必要分两种情况讨论.
2.1 当0≤v0如图3所示,带电小球的受力分析图.
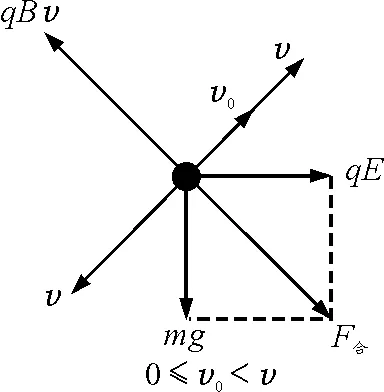
图3 受力分析
如图4所示,易知,小球一边从初始位置开始以速度大小为v-v0逆时针方向做匀速圆周运动,一边以速度v沿x轴正方向的匀速直线运动,匀速圆周运动轨迹在坐标系xOy的x轴的下方

(1)
(2)
(3)
(4)
(5)

图4 运动分解
经过时间t,小球位置在沿x轴正方向做匀速直线运动的新坐标系x′O′y′中的坐标为
x′=-Rsinωt
(6)
y′=Rcosωt
(7)
因此换算到xOy坐标系中的坐标为
x=vt+x′=vt-Rsinωt
(8)
y=-(R-y′)=y′-R=Rcosωt-R
(9)
整理可得
(10)
(11)
2.2 当v0>v时
如图5所示,带电小球的受力分析图.
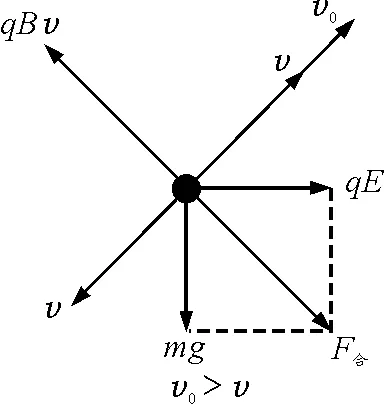
图5 受力分析
如图6所示,此时可认为小球一边从初始位置开始以速度大小为v0-v逆时针方向做匀速圆周运动,一边以速度v沿x轴正方向的匀速直线运动,匀速圆周运动轨迹在坐标系xOy的x轴的上方,半径
(12)
在坐标系x′O′y′中小球的坐标为
x′=Rsinωt
(13)
y′=-Rcosωt
(14)

图6 运动分解
因此小球在坐标系xOy中的坐标为
x=vt+x′=vt-Rsinωt
(15)
y=y′+R=-Rcosωt+R
(16)
整理可得
(17)
(18)
由以上分析可知,两种情况下小球的轨迹的参数方程的形式完全相同.
从上面的轨迹参数方程可以看出,轨迹形状显然与v0的取值是有关联的.如图7所示,在“仿真物理实验室”软件中设置好如下参数: 小球质量m=0.5 kg,小球电荷量Q=1 C,匀强电场电场强度E=5 N/C,匀强磁场磁感应强度B=1 T,重力场:g=10 m/s2,小球初始坐标(10 m,10 m).
图7 设置参数
3 “仿真物理实验”尝试
在0≤v03.1 尝试1
取特殊值v0=0,运行实验,结果轨迹如图8所示.

图8 取v0=0时运行结果
这显然是圆滚线(又称旋轮线、摆线).
理论研究释疑:
如图9所示,小球在轨迹的最低点具有沿x轴正方向最大速度2v,最低点轨迹切线沿x轴正方向;小球在轨迹的最高点速度为零,轨迹切线的斜率k不存在或不唯一,最高点为极大值点,最高点不光滑应为尖点.

图9 v0=0运动分析
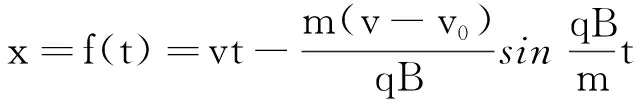
(19)
(20)
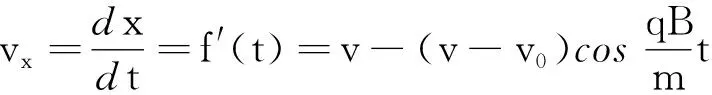
(21)
(22)
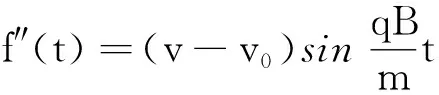
(23)
(24)
由轨迹方程的二阶导数知
(25)
当v0=0时代入
(26)
因此除轨迹的最高点vx=0外, 其余点由于vx>0,则在该运动区间
(27)
由高等数学可知,图像无拐点,且曲线轨迹向上凹,与仿真物理实验结果很吻合.
3.2 尝试2
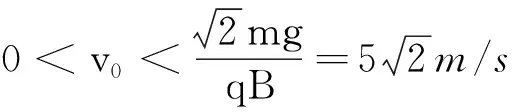

图10 取v0=3 m/s时运行结果
这种轨迹显然与尝试1不同.
理论研究释疑:
如图11所示,小球在轨迹的最低点速度为2v-v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为v0,方向也沿x轴正方向,最高点轨迹切线自然也水平.故这种情况轨迹可能存在拐点.
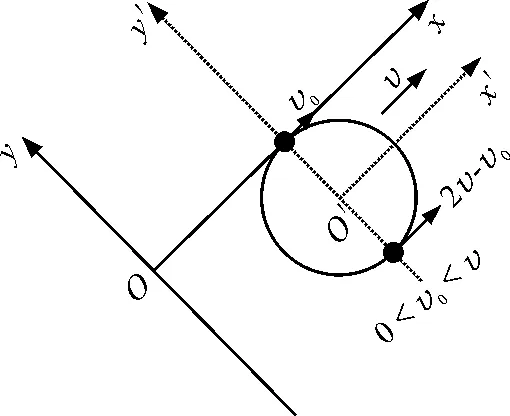
图11 0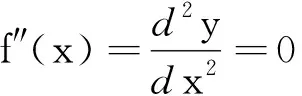
(28)
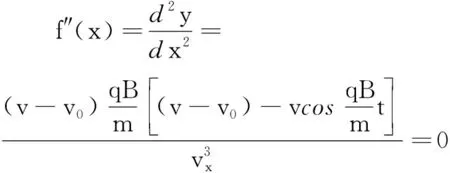
(29)
因为vx>0
(30)
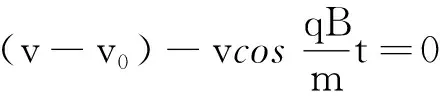
(31)
可得
(32)
(33)

(34)

(35)
容易得到,在拐点的左侧
(36)
曲线轨迹向下凹;
在拐点的右侧
(37)
曲线轨迹向上凹;与仿真物理实验得到的轨迹吻合.
接下来在v>v0范围内,分多种情况尝试.
3.3 尝试3
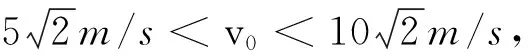

图12 取v0=11 m/s时运行结果
明显该曲线轨迹与上面尝试1、尝试2情况均不相同,是一种新的运动轨迹.
理论研究释疑:
如图13所示,小球在轨迹的最低点速度为v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为2v-v0,方向也沿x轴正方向,最高点轨迹切线自然也水平.故这种情况轨迹仍然可能存在拐点.
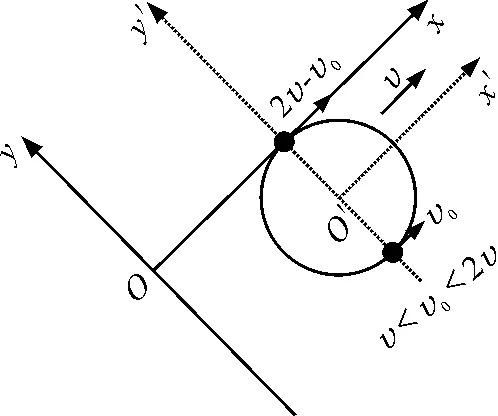
图13 v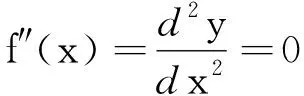
(38)

(39)
因为vx>0
(40)
(41)

(42)
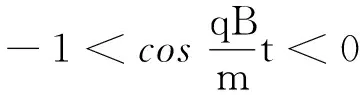
(43)

(44)

(45)
容易得到,在拐点的左侧
(46)
曲线轨迹向上凹;
在拐点的右侧
(47)
曲线轨迹向下凹;与仿真物理实验轨迹吻合.
3.4 尝试4

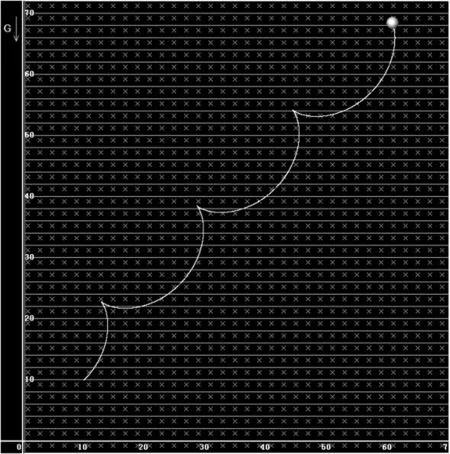
图14 取时运行结果
明显这个曲线在尝试1,尝试2,尝试3这3种情况中也未曾出现,也是一种新的运动轨迹.
理论研究释疑:
如图15所示,小球在轨迹的最低点具有沿x轴正方向最大速度v0=2v,最低点轨迹切线沿x轴正方向;小球在轨迹的最高点速度也出现为零,轨迹切线的斜率k不存在或不唯一,最高点为极大值点,最高点不光滑出现尖点.这时因为vx>0,当
v0=2v
(48)
时,代入得
(49)

图15 v0=2v运动分析
因此除轨迹的最高点vx=0外,其余点由于vx>0,则在该运动区间有
(50)
由高等数学可知,图像无拐点,且曲线轨迹向上凹,与实验结果吻合.
3.5 尝试5
当v0>2v时,取v0=20 m/s代入“仿真物理实验室”运行,结果轨迹如图16所示.

图16 取v0=20 m/s时运行结果
明显这个曲线在尝试1,尝试2,尝试3,尝试4种情况中均未出现,也是一种新的运动轨迹.
理论研究释疑:
如图17所示,可知,小球在轨迹的最低点速度为v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为v0-2v,方向沿x轴负方向,最高点轨迹切线自然也水平.这种情况小球有段时间向x轴正方向运动,有段时间向x轴负方向运动,在轨迹的最高点下方存在x轴分速度为零而y轴分速度不为零的特殊点,在这些点轨迹的切线沿y轴正或者负方向.
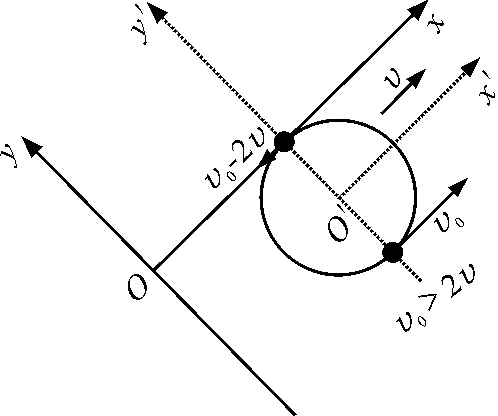
图17 v0>2v时运动分析

(51)
容易得到,若vx>0时
(52)
曲线轨迹向上凹;
在拐点的右侧,
(53)
曲线轨迹向下凹,与仿真物理实验轨迹吻合.
最后可以随便赋予小球任意速度,理论和仿真实验均表明无更多可能轨迹.下面将5种实验尝试情况下的5个相同小球赋值以上讨论的5个不同速度,一起运行试验得到所有可能的轨迹如图18所示.

图18 5种实验尝试情况下运行结果
4 结束语
在有些复杂的物理问题研究中,人脑的想象空间是非常有限的,借助“仿真物理实验”,先对未知领域进行尝试,获得感性的认知,然后借助理论研究寻找形成原因,这种方法可以帮助解决一些疑难问题,对于物理问题的研究未尝不是一个行之有效的策略.
猜你喜欢
圆锥曲线的切线方程及其推广的结论中学生数理化(高中版.高二数学)(2021年2期)2021-03-19 杨鹤鸣书香两岸(2020年3期)2020-06-29 切线在手,函数无忧新世纪智能(数学备考)(2020年12期)2020-03-29 最高、最低点重叠度计算的分析研究科技创新与应用(2019年24期)2019-10-24 巧析竖直平面内的圆周运动新课程·中旬(2017年12期)2018-03-07 过圆锥曲线上一点作切线的新方法课程教育研究(2017年26期)2017-08-02
如图3所示,带电小球的受力分析图.

图3 受力分析
如图4所示,易知,小球一边从初始位置开始以速度大小为v-v0逆时针方向做匀速圆周运动,一边以速度v沿x轴正方向的匀速直线运动,匀速圆周运动轨迹在坐标系xOy的x轴的下方

(1)
(2)
(3)
(4)
(5)

图4 运动分解
经过时间t,小球位置在沿x轴正方向做匀速直线运动的新坐标系x′O′y′中的坐标为
x′=-Rsinωt
(6)
y′=Rcosωt
(7)
因此换算到xOy坐标系中的坐标为
x=vt+x′=vt-Rsinωt
(8)
y=-(R-y′)=y′-R=Rcosωt-R
(9)
整理可得
(10)
(11)
2.2 当v0>v时
如图5所示,带电小球的受力分析图.

图5 受力分析
如图6所示,此时可认为小球一边从初始位置开始以速度大小为v0-v逆时针方向做匀速圆周运动,一边以速度v沿x轴正方向的匀速直线运动,匀速圆周运动轨迹在坐标系xOy的x轴的上方,半径
(12)
在坐标系x′O′y′中小球的坐标为
x′=Rsinωt
(13)
y′=-Rcosωt
(14)

图6 运动分解
因此小球在坐标系xOy中的坐标为
x=vt+x′=vt-Rsinωt
(15)
y=y′+R=-Rcosωt+R
(16)
整理可得
(17)
(18)
由以上分析可知,两种情况下小球的轨迹的参数方程的形式完全相同.
从上面的轨迹参数方程可以看出,轨迹形状显然与v0的取值是有关联的.如图7所示,在“仿真物理实验室”软件中设置好如下参数: 小球质量m=0.5 kg,小球电荷量Q=1 C,匀强电场电场强度E=5 N/C,匀强磁场磁感应强度B=1 T,重力场:g=10 m/s2,小球初始坐标(10 m,10 m).

图7 设置参数
3 “仿真物理实验”尝试
在0≤v0 取特殊值v0=0,运行实验,结果轨迹如图8所示. 图8 取v0=0时运行结果 这显然是圆滚线(又称旋轮线、摆线). 理论研究释疑: 如图9所示,小球在轨迹的最低点具有沿x轴正方向最大速度2v,最低点轨迹切线沿x轴正方向;小球在轨迹的最高点速度为零,轨迹切线的斜率k不存在或不唯一,最高点为极大值点,最高点不光滑应为尖点. 图9 v0=0运动分析 (19) (20) (21) (22) (23) (24) 由轨迹方程的二阶导数知 (25) 当v0=0时代入 (26) 因此除轨迹的最高点vx=0外, 其余点由于vx>0,则在该运动区间 (27) 由高等数学可知,图像无拐点,且曲线轨迹向上凹,与仿真物理实验结果很吻合. 图10 取v0=3 m/s时运行结果 这种轨迹显然与尝试1不同. 理论研究释疑: 如图11所示,小球在轨迹的最低点速度为2v-v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为v0,方向也沿x轴正方向,最高点轨迹切线自然也水平.故这种情况轨迹可能存在拐点. 图11 0 (28) (29) 因为vx>0 (30) (31) 可得 (32) (33) (34) (35) 容易得到,在拐点的左侧 (36) 曲线轨迹向下凹; 在拐点的右侧 (37) 曲线轨迹向上凹;与仿真物理实验得到的轨迹吻合. 接下来在v>v0范围内,分多种情况尝试. 图12 取v0=11 m/s时运行结果 明显该曲线轨迹与上面尝试1、尝试2情况均不相同,是一种新的运动轨迹. 理论研究释疑: 如图13所示,小球在轨迹的最低点速度为v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为2v-v0,方向也沿x轴正方向,最高点轨迹切线自然也水平.故这种情况轨迹仍然可能存在拐点. 图13 v (38) (39) 因为vx>0 (40) (41) (42) (43) (44) (45) 容易得到,在拐点的左侧 (46) 曲线轨迹向上凹; 在拐点的右侧 (47) 曲线轨迹向下凹;与仿真物理实验轨迹吻合. 图14 取时运行结果 明显这个曲线在尝试1,尝试2,尝试3这3种情况中也未曾出现,也是一种新的运动轨迹. 理论研究释疑: 如图15所示,小球在轨迹的最低点具有沿x轴正方向最大速度v0=2v,最低点轨迹切线沿x轴正方向;小球在轨迹的最高点速度也出现为零,轨迹切线的斜率k不存在或不唯一,最高点为极大值点,最高点不光滑出现尖点.这时因为vx>0,当 v0=2v (48) 时,代入得 (49) 图15 v0=2v运动分析 因此除轨迹的最高点vx=0外,其余点由于vx>0,则在该运动区间有 (50) 由高等数学可知,图像无拐点,且曲线轨迹向上凹,与实验结果吻合. 当v0>2v时,取v0=20 m/s代入“仿真物理实验室”运行,结果轨迹如图16所示. 图16 取v0=20 m/s时运行结果 明显这个曲线在尝试1,尝试2,尝试3,尝试4种情况中均未出现,也是一种新的运动轨迹. 理论研究释疑: 如图17所示,可知,小球在轨迹的最低点速度为v0,方向沿x轴正方向,最低点轨迹切线水平;小球在轨迹的最高点速度为v0-2v,方向沿x轴负方向,最高点轨迹切线自然也水平.这种情况小球有段时间向x轴正方向运动,有段时间向x轴负方向运动,在轨迹的最高点下方存在x轴分速度为零而y轴分速度不为零的特殊点,在这些点轨迹的切线沿y轴正或者负方向. 图17 v0>2v时运动分析 (51) 容易得到,若vx>0时 (52) 曲线轨迹向上凹; 在拐点的右侧, (53) 曲线轨迹向下凹,与仿真物理实验轨迹吻合. 最后可以随便赋予小球任意速度,理论和仿真实验均表明无更多可能轨迹.下面将5种实验尝试情况下的5个相同小球赋值以上讨论的5个不同速度,一起运行试验得到所有可能的轨迹如图18所示. 图18 5种实验尝试情况下运行结果 在有些复杂的物理问题研究中,人脑的想象空间是非常有限的,借助“仿真物理实验”,先对未知领域进行尝试,获得感性的认知,然后借助理论研究寻找形成原因,这种方法可以帮助解决一些疑难问题,对于物理问题的研究未尝不是一个行之有效的策略.3.1 尝试1


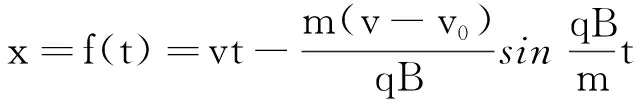
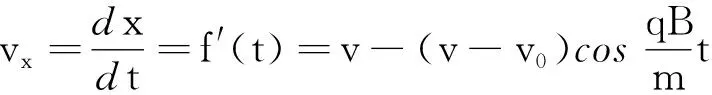
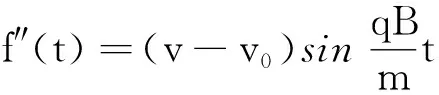
3.2 尝试2
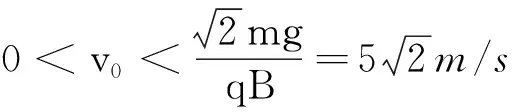


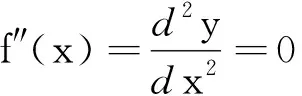
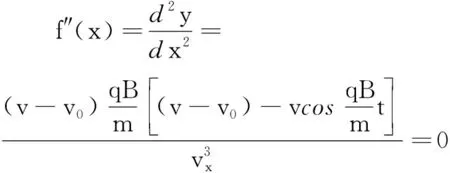
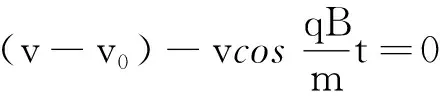


3.3 尝试3
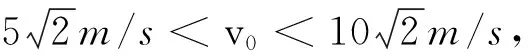


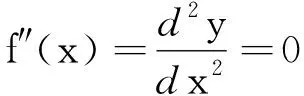


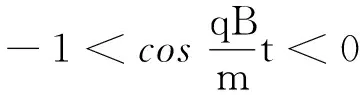


3.4 尝试4



3.5 尝试5




4 结束语

