EM-KNN算法在复烤烟叶分类上的运用
张 慧,侯开虎,周 洲
(昆明理工大学,机电工程学院,云南 昆明 650000)
0 引言
K-近邻(K-Nearest Neighbor,KNN)算法机器学习中解决分类问题的常用方法之一,KNN算法最早是由Cover和Hart在20世纪六十年代提出,在理论上算比较成熟的分类方法。KNN算法的分类原理是通过与分类对象最近的训练样本k来实现分类k一般选择大于 3的任意数,样本之间的空间距离一般采用 Euclidean 距离的计量方式,所要分类的对象以k个样本为依据分类[1]。KNN算法省去了需要预先建立模型的步骤,与其他的机器学习算法相比具有简单高效、不需要进行训练等优点,在分类问题上被广泛使用[2-5]。但传统的KNN算法依然存在很多的不足:在计算时储存参与计算的每一个样本,耗费了极大的储存空间[6];KNN的计算原理决定了待分类样本要与每一个样本进行距离的计算,其计算量大;由于样本的分配不均衡问题,可能造成分类结果失准[7];需要通过计算不同的 k值的预测能力来选择不同的k值,算法对不同k值的响应较灵敏,一般使用较小的k值,因此,在进行KNN算法前要确定一个确定k的值,多数情况下是由经验选择[8]。
为了解决KNN算法存在的问题,对KNN算法的优化一直是许多学者关注的问题,主要从两个角度进行优化,原始KNN算法得出的k个最近样本中是以少数服从多数的思想确定被分类样本的类别,就会存在一些干扰样本导致了分类的不精确,所以优化 KNN算法的第一个角度是对所给样本进行剪枝,樊存佳等人[9]采用改进了的 K-Medoids聚类算法对分类中贡献度低但影响分类结果的样本进行裁剪,定义了度函数对测试文本的最近邻文本进行有差别的处理,以此提高了KNN算法的计算速度和分类准确度,但这种方法有可能会过度裁剪;余鹰等人[10]通过引入变精度粗糙集模型,将训练样本划分为核心数据块和边界数据块,以此减小分类的干扰,增强 KNN算法的鲁棒性,该算法更适用于球状数据;耿丽娟等人[11]提出对样本进行分层分类,最后一层的决策采用差分的方法,并用实例证明该方法在大数据分类下的有效性;严晓明等人[12]提出了类别平均距离的加权KNN算法,采用所属类别的平均距离与待分类样本和训练样本的距离差值比,大于设定的阈值,就将此样本从原样本中剔除。原始的KNN算法采用欧氏距离计算样本的距离,忽略了样本数据特征指标之间的相关性,欧氏距离的计算是基于所有的特征指标,然而在分类时实例也包含了与分类不相关的属性,这时欧式距离分类就会变得不准确,第二个优化的角度就是针对样本数据之间的距离进行优化,谢红等[13]提出的基于卡方距离的KNN算法,并采用灵敏度对指标赋权,克服了欧式距离的不足;肖辉辉等[14]将欧氏距离测量改为基于特征指标相关距离,有效的度量了样本之间的相似度;另外曾俊杰等在[15]提出基于马氏距离、王帮军等[16]提出基于改进协方差特征的 KNN算法,许杞刚等[17]采用多项式函数与欧氏距离相结合的方法进行距离度量。
本文是在上述研究的基础之上,考虑到各种距离方法在 KNN算法的计算上没有考虑过分类特征指标的权重问题,因此本文加入了特征指标的熵值法赋权对KNN算法进行改进,提出了EM-KNN算法,并且在基于python语言的Jupyter Notebook交互式 WEB端对复烤烟叶按化学成分的分类问题上运用 EM-KNN分类算法分析,并检验算法的合理性,突出改进的算法在提高复烤烟叶的分类精度上,优胜于传统的KNN分类算法。
1 KNN算法
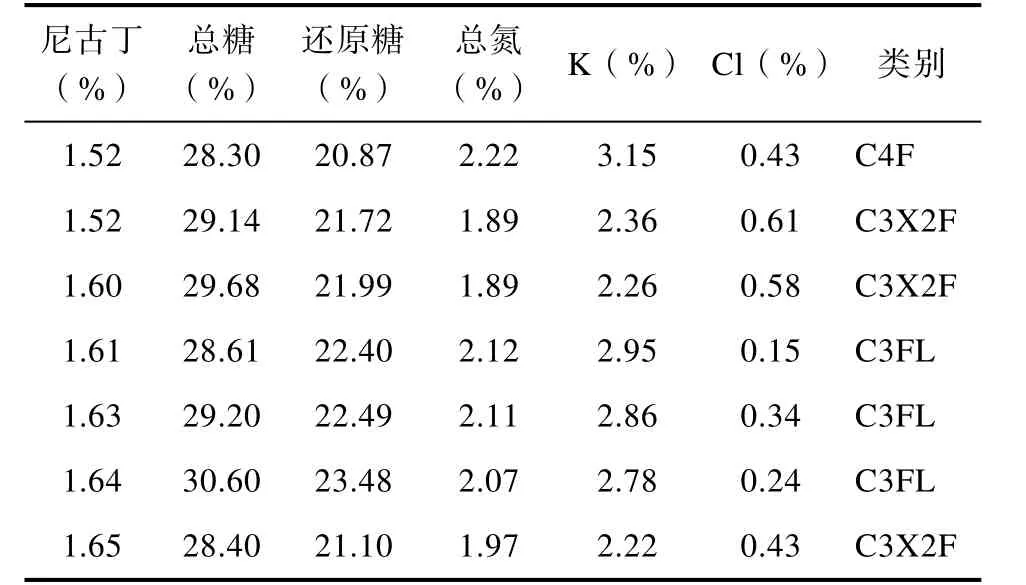
KNN算法的工作原理是:存在一个已经知道所属分类的训练样本集,输入待分类样本,计算待分类样本与训练样本集中每一个训练样本之间的距离,然后算法提取与待分类样本最近邻的k个样本,一般只取最相近的前k个数据,一般2 KNN算法中关键的就是计算待分类样本与训练样本的距离,本文中所涉及到常用的距离度量方法有欧式距离、曼哈顿距离、闵可夫斯基距离[19]。设存在两个 n维向量 X,Y,令 X=(X1,X2,…, Xn),Y=(Y1,Y2,…, Yn),各种距离度量公式如下所示: (1)Euclidean距离 欧氏距离全称为欧几里得距离, X,Y的欧氏距离定义为: (2)Manhattan距离 曼哈顿距离,又称城市距离,X,Y的曼哈顿距离定义为: (3)Chebyshev距离 切比雪夫距离,X,Y的切比雪夫距离定义为: 设有m个数据样本,n个样本特征指标,有数据矩阵 M =( aij)m×n,信息论中,信息熵是系统无序程度的度量,信息是有序程度的度量,数值上二者互为相反数,样本中的某一特质指标的信息熵越大,表明该指标为决策所提供的信息量越小,相对应的权重越小,相对地,某一指标的信息熵越小,则该指标提供的信息量越大,权重就越大[20]。 熵值法的计算步骤是: (1)第j项指标下的第i个样本数据占j指标下总体样本的比重tij (2)计算第j项指标的信息熵hj (3)计算第j项指标的熵值ej 熵值法赋权属于客观赋权方法的一种,有效的避免了主观随意性对指标重要性的影响,所赋权值的大小是依据样本数据的分散情况而来,有较强的理论依据,但也存在如果数据之间跨度太大,其赋权结果与指标客观反应存在一定的差距,在本论文中的数据样本波动不大,不影响给样本的特征指标赋权,因此本文宜采用熵值法给样本特征指标赋权[21]。 基于传统的 KNN分类算法的基础上,考虑到传统的 KNN算法忽略了各个特征指标对分类结果的信息贡献程度不同,在传统的算法步骤中加入了熵值法给特征指标赋权,使分类算法更精确。 改进的KNN分类算法的步骤如下: (1)创建样本数据集,设数据集为S,Xi为训练样本集,i∈ [1 ,…, m ],数据集中包含 n个不同的分类类别,Yi为测试样本,i∈ [1 ,…, t ]每一个训练样本中包含m个特征指标。用熵值法计算样本数据的特征属性权重,赋权过程按照公式(4)-(8)的方式进行。 (2)给KNN算法中的k设定一个初值。 (3)用改进的距离度量公式计算每个测试样本和训练样本的距离,如特征赋权的欧氏距离公式为: (4)对计算出的距离进行排序,选取距离待分类样本最近的k个训练样本。 (5)按照所选择的k个训练样本所属的类别,以k个样本中占比最大的样本作为待分类样本的类别。 (6)根据待分类样本的分类结果,与实际的所属类别对比,计算分类器的准确率,计算准确率的公式为: 式中:B为分类准确的测试样本数,C为测试样本总数。 本文通过数据验证所改进的算法的准确性,在Jupyter Notebook交互式WEB端用python编写KNN分类算法器,将数据集导入分类器中,选取不同的K值对数据进行验证,整个验证过程分为两个部分,第一个部分采用原始的KNN算法对数据进行验证,分别用欧氏距离、标准化欧氏距离、曼哈顿距离、切比雪夫距离对待分类样本与训练样本的相似度进行度量,并计算出不同K值下分类的准确率。第二部分使用改进后的KNN算法,再分别对距离度量公式进行测试,将计算得到的不同K值下的准确率与第一个部分的结果进行比较,最后分析实验结果。 本文采用的数据样本是某烟叶复烤厂对复烤烟叶化学成分分析得到的数据,总的数据量是 749,分析的主要化学成分为尼古丁、总糖、还原糖、总氮、K、CL,也就是数据样本的特征指标数为 6,一共分为5个类,部分实验数据如表1所示,选择数据总量的1/3作为测试样本,其余的2/3作为训练样本。 表1 实验数据部分示例Tab.1 Example of experimental data 为了验证改进 KNN分类算法的有效性,验证过程中改变K值,分别用几种常见的距离度量公式度量样本之间的距离,验证过程中,每一个距离公式测试了10次,为了比较三种距离公式在复烤烟依据化学成分分类的效果,取10次验证的平均值,如表2所示。 从表2中可以看出,使用改进的基于三种距离度量方式 KNN分类算法在分类准确率上大致都得到了提高,在基于欧氏距离的KNN算法中效果最明显,准确率提升幅度最大的是当K=3时的基于欧氏距离的 KNN算法,说明改进的 KNN算法在提升KNN分类精确度上有很好的效果。无论是原始的KNN算法还是改进后的KNN算法,使用切比雪夫距离公式度量的分类精确率远远小于其他两种, 对于其他两种距离度量,选择K值为3或者5时,分类效果最佳。 为了更直观的评价改进KNN算法的分类效果,分别绘制了K取不同值的分类准确率折线图,由表2得出切比雪夫距离在此样本中的分类准确率太低,因此在下面的分析中只对欧氏距离和曼哈顿距离作比较。当k=3时,实验结果如图1所示;当k=5时,实验结果如图2所示;当k=8时,实验结果如图3所示。 表2 不同距离公式、不同K值的测试精确率(%)Tab.2 Test accuracy of different distance formulas and different K values (%) 图1 K值为3时结果准确率折线图Fig.1 Curve of the accuracy of the results when the K value is 3 由图1-图3可以看出在复烤烟叶依据化学成分分类的数据样本中,采用曼哈顿(Manhattan)距离公式的传统 KNN分类算法分类准确率总体优于基于欧氏距离(Euclidean)的算法,通过加入熵值法特征向量赋权后,两种距离公式算法的分类准确度都大大的提升了,欧氏距离KNN分类算法提高效果尤为显著,图1和图2显示出改进的Euclidean KNN算法在 10次的分类测试中准确率均高于传统的算法。算法未改进之前,两类度量距离算法在10次分类验证中结果准确率起伏较大,改进后,其分类准确率不仅得到了提高,其数据的平稳度也得到了提高,当K=5或K=8时改进效果较明显。 图2 K值为5时结果准确率折线图Fig.2 Curve of the accuracy of the results when the K value is 5 图3 K值为8时结果准确率折线图Fig.3 Curve of the accuracy of the results when the K value is 8 通过改进后的KNN算法与传统的KNN算法对复烤烟叶依据化学成分的分类中看出,改进后的KNN算法在分类精度上得到了很大的提升。在KNN算法中,K值的选取对分类的效果有直接的影响,小的K值会导致为待分类样本提供的信息太少而影响分类精度,由于KNN算法对待测样本的分类实行“少数服从多数”的原则,所以太大的K值会导致决定权掌握在选取的训练样本中的“多数”手中,也会出现不合理的分类,从图1-图3中可以看出,当K=3时,分类准确度失衡幅度最大,当K=8时次之,当K=5时,改进后的KNN算法的分类准确率起伏不大,较为平稳。由此可以得出,在对复烤烟叶依据化学成分的分类中,使用改进的基于欧氏距离的KNN算法中,当选取K=5,其分类效果最佳。 在KNN分类算法中,传统的KNN算法采用欧氏距离对样本之间的距离进行度量,由于数据样本的不同,每一个样本的特征指标在决定所属类别时提供的信息往往是不一样的,分类结果往往与实际相差甚远,因此本文提出一种基于熵值法对特征指标赋予权重的KNN分类算法(ME-KNN),通过分类准确度衡量分类效果,并在复烤烟叶依据化学成分的分类数据样本中进行分类算法的测试,结果显示ME-KNN算法分类效果得到了很大的提升,通过对三种分类距离公式的测试,在本文采用的数据样本中基于欧式距离的ME-KNN算法分类效果最佳。1.1 距离度量


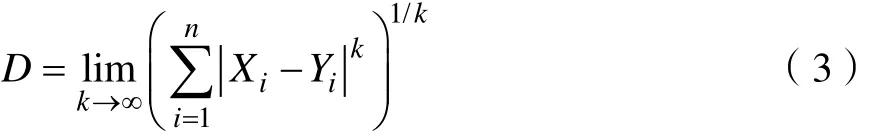
2 熵值法赋权的KNN算法
2.1 熵值法



2.2 改进的KNN算法


3 实例验证
3.1 实验数据
3.2 对比分析


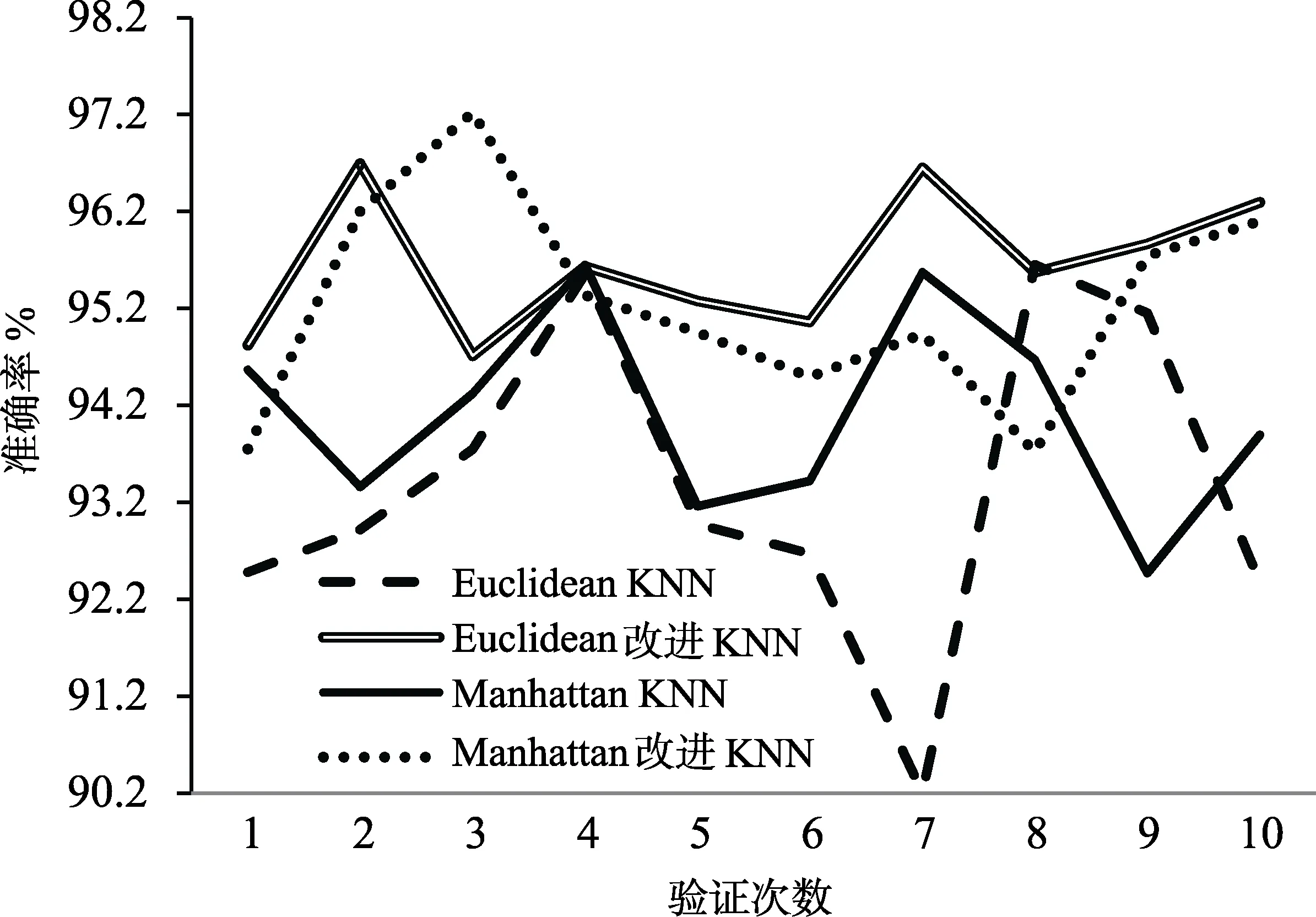
3.3 实验结果

4 结论

