基于方体剖分和量子免疫粒子群算法的Nash均衡求解

刘露萍，贾文生*

（1. 贵州大学 数学与统计学院，贵州 贵阳　550025，2. 贵州省博弈决策与控制系统重点实验室，贵州 贵阳　550025）

0　引言

1944年，美国著名学者冯诺依曼（Von Neumann）和摩根斯坦（Morgenstern）的名著《博弈论与经济行为》中提到：“博弈论是建立经济行为理论的最恰当方法”。特别值得关注的是自1994年至今，诺贝尔奖多次颁给博弈论的研究学者。纳什（Nash）、泽尔腾（Selten）、海萨尼（Harsanyi）因在非合作博弈论研究领域作出贡献获得了 1994年诺贝尔经济学奖，紧接着1996年颁给博弈论和信息经济学家莫里斯（Mirrless）和维可瑞（Vickrey），2001年颁给了对充满不对称信息市场进行分析的博弈论学者阿克尔洛夫（Akerlof）、斯彭斯（Spence）和斯蒂格利茨（Stiglitz），2005年颁给博弈论著名学者奥曼（Aumann）和谢林（Schelling），2007年颁给机制设计方面做出突出贡献的博弈论学者赫维克（Hurwicz）、马斯金（Maskin）和迈尔森（Myerson），2012年颁给沙普利（Shapley）和罗斯（Roth），2014年颁给用博弈论分析产业组织理论的学者梯若尔（Tirole），2017年诺贝尔经济学奖得主 Richard Thaler也是在博弈论领域做出突出贡献，特别是在“有限理性行为”方面成就斐然。1950年，纳什（Nash）在他的博士论文中提出了非合作博弈模型和解的概念，后来被人们称之为Nash均衡。Nash均衡是非合作博弈的核心概念，也奠定了n人非合作博弈理论的坚实基础。Nash均衡不仅对社会科学领域影响巨大，也对包括计算机科学、人工智能、大数据等领域产生了重大影响，几乎影响到科学研究的所有领域。

1　模型描述

特别地，对于2人的有限非合作博弈，即双矩阵博弈：设参与人 1的混合策略为 x=( x1,x2,…,xm)∈X，参与人2的混合策略为y= ( y1, y2,…,yn)∈Y，Am×n，Bm×n分别为参与人1和参与人2的支付矩阵，则参与人1和参与人2的期望收益分别为 x AyT和 x ByT。

定义 1[1]x*是有限n人非合作博弈模型的一个Nash均衡，如果x*满足… ,n )，其中x*xi表示在均衡解的条件下只有博弈参与人i用 xi替换均衡解x*中自己的策略，其他博弈参与人都不改变各自在均衡解中的策略。

引理 1[1]混合策略x*是有限n人非合作博弈的一个Nash均衡的充分必要条件是：对于任意参与i的每一个纯策略。

特别地，（x*,y*）是双矩阵博弈的一个 Nash均衡的充分必要条件是：

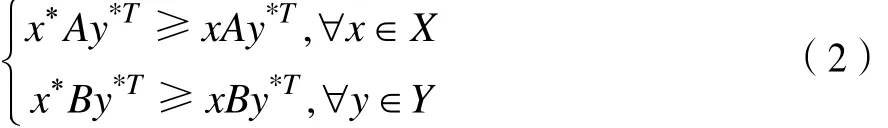
2　方体剖分算法的基本思想和实现步骤

Step 1对每一个博弈参与人i∈N，对包含其策略集 Xi的方体[0,1]mi的每一维进行m等分剖分，这样就得到如下的一个分划：

Step 3因 μi(x )是关于x的多线性函数，所以是连续的，从而在每一个小闭区间上是一致连续的，所以可以用 μi( y )来任意近似，而划分是有限的，必然也是有限的，因此，一定可以在有限步骤内找到有限n人非合作博弈的近似Nash平衡点。具体来说，对于任意给定的精度ε＞0，存在，使得当对任意的 i ∈{1,2,…,n}，j∈ { 1,2,… ,mi}满足＜δ时，有

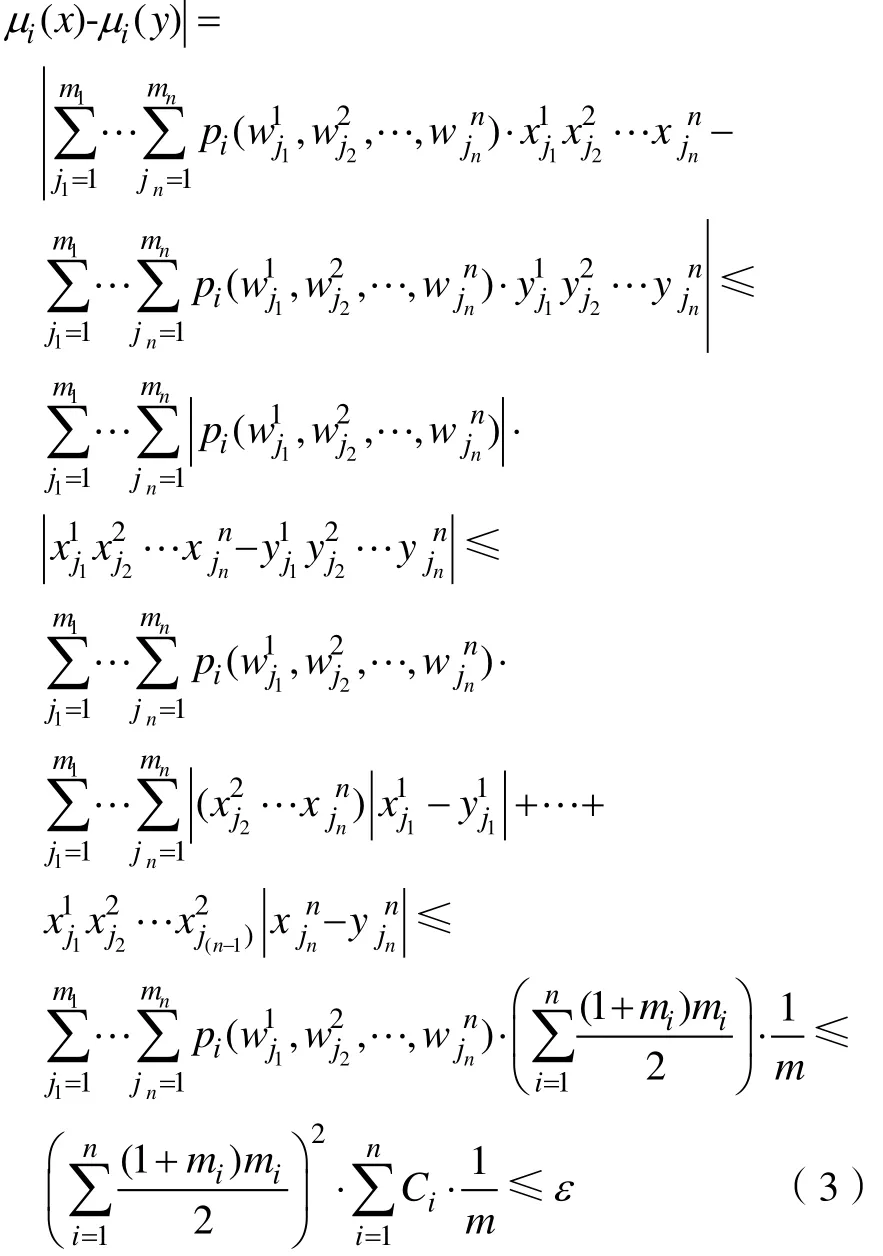
这样，对每一个博弈参与人iN∈，对包含其策略集iX的方体[0,1]im的每一维进行m等分剖分，只一定可以达到相应的精度ε。

3　结合量子免疫粒子群算法的实例分析

Nash均衡的算法和实现路径研究，是当前国际博弈论研究领域的热点和前沿之一。许多学者围绕Nash均衡的计算和实现做了大量的工作，提出了各种各样的算法[2-11]，但是主要分为两大类。一类是纯数学分析算法，主要借助于梯度、同伦、投影和罚函数等技巧来计算和分析。这类算法的对函数的可微性和凹凸性等性质要求高，由实际问题建立的博弈模型往往不一定满足这些要求。另一类是智能算法，特别是生物演化算法，这类算法不但实现简单，而且更重要的是代表着一种新的方向，因为从演化和学习的角度将 Nash均衡看成是具有有限理性的博弈参与人逐步寻求最优解的结果更贴近现实。关于粒子群算法也有很多改进和应用[11-15]，特别是文献[12]提出了一种新的量子免疫粒子群算法，该算法将量子不确定性理论和免疫粒子群算法结合，为Nash均衡的实现路径研究提供了一种新的探索。现在将改进的量子免疫粒子群算法与方体剖分算法结合，对下面的算例进行计算和分析：

例考虑博弈 Γ (X, Y, A, B)，

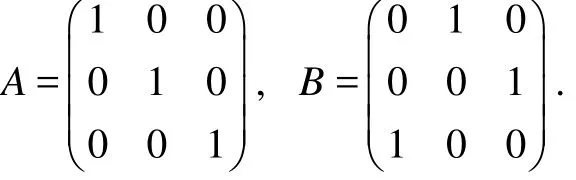
利用上述方体剖分算法得到的近似 Nash平衡点为：

(x,y)=(0.33333, 0.33333, 0.33333, 0.33333,0.33333, 0.33333)。

具体的计算搜索路径如图1所示：

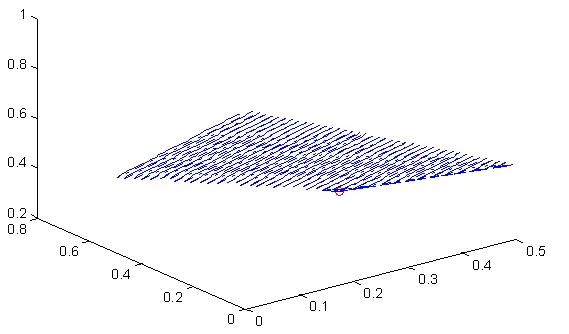
图1　博弈 Γ ( X, Y, A, B)的方体剖分算法3维搜索路径图Fig.1　Cube Subdivision Algorithm of Game　 Γ( X, Y, A, B)

总之，通过实际算例的计算和分析，可以看出本文提出的方体剖分算法和量子免疫粒子群算法结合在求解有限n人非合作博弈 Nash均衡方面是有效的。而且把一个有限n人非合作连续型博弈通过对混合策略空间的方体剖分转化为一个离散形式的有限博弈，给出了连续型博弈的一种近似可计算性结果，并借助量子免疫粒子群算法给出了具体的求解路径。

4　结论

本文提出的方体剖分算法与以往文献中的单纯形剖分算法不同，单纯形剖分算法的关注点和基础在于利用不动点理论和单纯形剖分来计算近似Nash均衡，而且它的适用范围往往受到博弈支付函数表达形式的限制。另外，从方体剖分算法的设计过程看，其本质就是把一个连续型博弈通过对混合策略空间的方体剖分转化为一个离散形式的有限博弈，因此该算法的主要意义在于从某种意义上给出了连续型博弈的一种近似可计算性结果，而且算法较为直接，更容易推广到一般的连续函数博弈，同时本文结合了量子免疫粒子群算法给出了具体算例的Nash均衡的搜索路径。