基于核加权KNN和多目标优化的众包平台定价系统设计

彭云聪，任心晴，石浩森

（南京邮电大学，江苏 南京　210046）

0　引言

当下，众包模式以其自由、合作、碎片化工作等特点，越来越受到企业的青睐。众包指公司或机构把过去员工的工作，以自由自愿形式外包给非特定的大众的一种大型网络运营模式[1]。它大大提高了经济效率，更是一种未来的商业模式。

国内对众包模式的研究主要体现在众包的概念[2]、参与活动的用户行为模式[3]和任务定价规律等方面。王桂云等人研究了任务设计、发布方信誉和不同平台对参与者行为的影响[4]；胡静思等人则提出了基于双边市场理论的众包平台定价策略[5]，重点讨论了网络外部性、用户归属、平台差异化以及平台技术对定价的影响。而孙信听等人则采用解决多臂赌博机的方法确定任务定价规则，基于贪婪算法对任务进行分配以达到平台收益的最大化[6]。

本文参考 2017年高教社杯全国大学生数学建模竞赛数据，以“拍照赚钱”众包平台为例，基于题目所给出的地理位置信息、用户情况、历史订单详情等，研究众包模式下任务的最优定价问题[7]。考虑任务的位置、任务价格和任务难度为影响任务完成情况的因素，建立基于多项式核函数的加权KNN[8]模型和多目标优化模型，最后通过有序样本聚类法[9]，确定最优任务定价规则。综上所述，合理构建众包平台定价系统，一定程度上对解决该类问题起参考作用。

1　核加权KNN分类预测模型

1.1　指标确立

研究表明一般任务价格和任务完成情况主要取决于任务类型、任务颗粒度和任务难度[10]，因此可以通过上述三个方面定量化的指标，制定合理的价格。如果当前价格与合理价格偏差过大，那么就可能出现无人接单的情况。

图1　指标关系图Fig.1　Index relation diagram

本文不考虑打包发布，忽略任务颗粒度的影响，选取任务经度、纬度、附近用户人数、当前任务价格作为定量指标，任务完成情况作为判别结果。由于数据间存在较大的量纲差异，将数据进行标准化预处理。当前定价方案下，任务完成率约60%。

1.2　传统的KNN模型

根据样本数据特点，通过经验分析，基于KNN的判别模型较为合适。为了对任务完成情况进行判别分析，引入映射

其中xi为样本， f （Xi）为样本完成情况的预测值

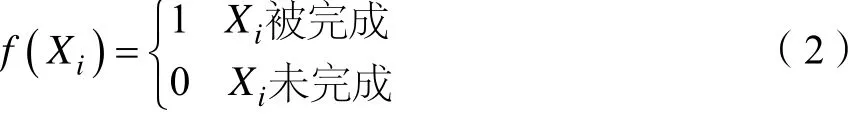
KNN决策规则为

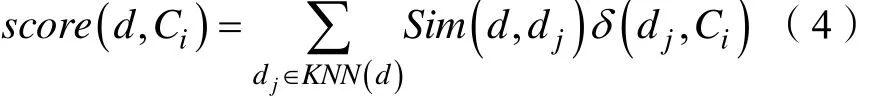
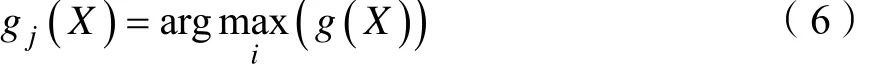
其中

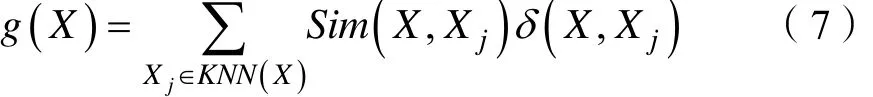
1.3　核加权KNN分类模型

在构造距离量度过程中只涉及到样本点之间的点积运算，同时考虑到数据可能低维不可分，所以引入多项式核函数，利用φ()·将数据样本投射到高维特征空间 F，通过在F中基于准则构造新的分类函数，解决在初始空间线性不可分的问题。

用核函数替代内积运算，核函数为

本文定义多项式核函数为

此时参数d决定了模型的适应性，若选择不当，会降低预测精度。

定义样本间距离量度为

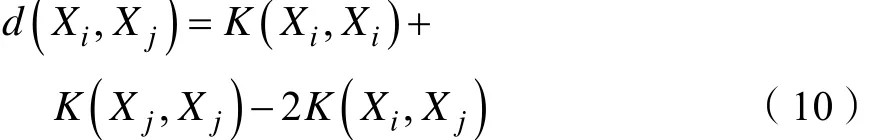
根据样本的距离量度，在训练样本中找到每个样本的k个近邻样本，分别计算出相应的权值[12]，通过高斯函数定义权值为

式中d为两样本之间的距离量度，ac、为任意常数，决定了权值变化趋势速度。

最后求出该样本的k个近邻样本的加权平均

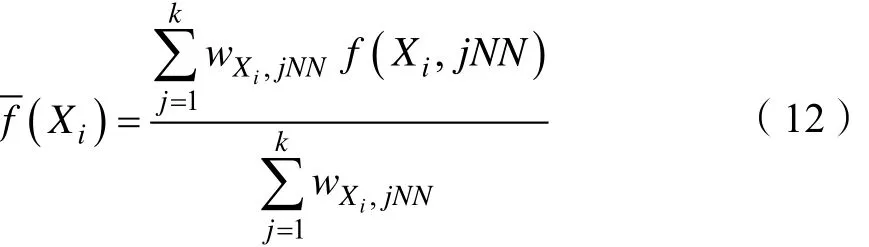
将每个测试样本的加权平均与阈值 t比较，样本较为均衡情况下阈值一般取0.5，若f≤t，则判定该任务未被完成。核加权KNN分类法对测试样本的k个近邻样本给予不同权重，权重随着近邻样本点和测试样本之间的距离量度的改变而呈负指数函数改变。

1.4　参数的优化

每个样本近邻数k和多项式核函数次数d的确定，是基于核函数的加权KNN模型建立的关键。为了提高精度和泛化能力，需要对参数进行优化处理。

参数k对分类器的精度有着重要的影响，利用遍历法结合交叉验证对参数 k的不同取值进行测试，以分类精度为标准，当k为4时，预测精度达到较高的水平。

通常情况下，参数d为大于1的整数，但由于实际问题的特殊性，为了使模型精度较高，有较好的鲁棒性，假设它为区间[0,5]上的任意一个实数。采用粒子群优化算法[13](PSO)来确定参数 d，其步骤为：

Step1: 初始化粒子群体，包括随机位置和速度；

Step2: 计算当前情况下的分类器的误差率，判断是否更新历史最佳位置和全局最佳位置；

Step3: 通过公式计算下一次每个粒子的位置，当迭代达到规定次数或误差率减小不显著则寻优结束，如果不满足结束条件，那么返回Step2。

通过迭代搜寻最优值，最后寻得最优 d值为1.93，如图2。

1.5　模型检验

本文选取了核加权 KNN模型，采用交叉验证法，将其分类预测精度与其他分类器相比，如表1，说明了核加权KNN分类模型的优越性。

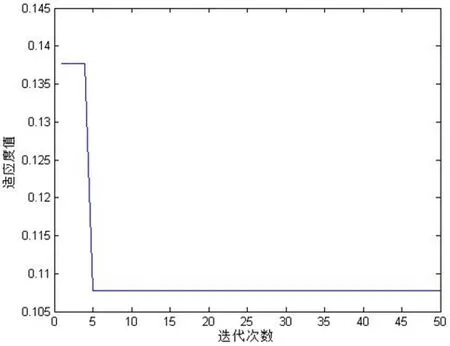
图2　适应度进化曲线Fig.2　Fitness evolution curve

考虑到NFL定理，我们使用多种代表性分类方法采用交叉验证法对比精度，可以看出对当前问题，本文构建的核加权KNN模型是最适宜的解决方法。

表1　不同分类器的预测精度Tab. 1　Prediction accuracy of different classifiers

2　基于多目标优化的最优定价方案

2.1　多目标规划模型

任务完成率和每个任务的收益是反映经营模式的经济效益的重要标准，而任务完成率又与任务价格正相关，所以两者存在相互制约的关系。

由于每个任务的成本价格未知，并且众包平台不一定要每一单利润大于 0，对于初起步的平台，任务的完成率及其效应至关重要，所以不能简单地通过利润最大化来建立目标函数。因此，根据完成率最大，提升价格最少为目标建立优化模型。

· 任务完成率是指在不同定价方案情况下，完成任务数与总任务数的比值，属于效益型指标，而新定价方案的完成数通过核加权 KNN分类模型仿真预测得出。根据映射

任务完成率目标函数为

式中n为任务总数

· 新方案的任务总价格与原来总价基础上的任务加价是一致的，简便起见，考虑加价情况即可，设每个未完成任务提高价格为 p （ Xi），那么所有任务的加价为

因此，最终优化目标为

2.2　基于贪心法的增益分析求解

对于多目标优化，常采用线性加权和法、分层法等，但是加权和法需要确定各个指标的权值，本文指标量纲差异较大，权重不易确定，缺少理论依据；而带宽容的分层多目标优化法中宽容程度的确定主观性太强。因此本文提出了一种基于贪心法的增益分析。

对平台发展而言，任务完成率目标函数更重要，因此利用价格变动情况下判别函数（）fX的结果，结合贪心法得到每增加 1%的任务完成率下最低的加价金额。如图 3，可以看出每个任务完成率下的价格增益情况。

2.3　基于有序样本聚类法最优分割点的选择

观察图 3，较难判断出最优分割点，使其分为加价合理与加价不合理的两部分，因此采用有序样品聚类分析法——将每提升 1%任务完成率所需要加价金额按序排列，记为，从而进行有序样本最优聚类，其临界点即为最优分割点。

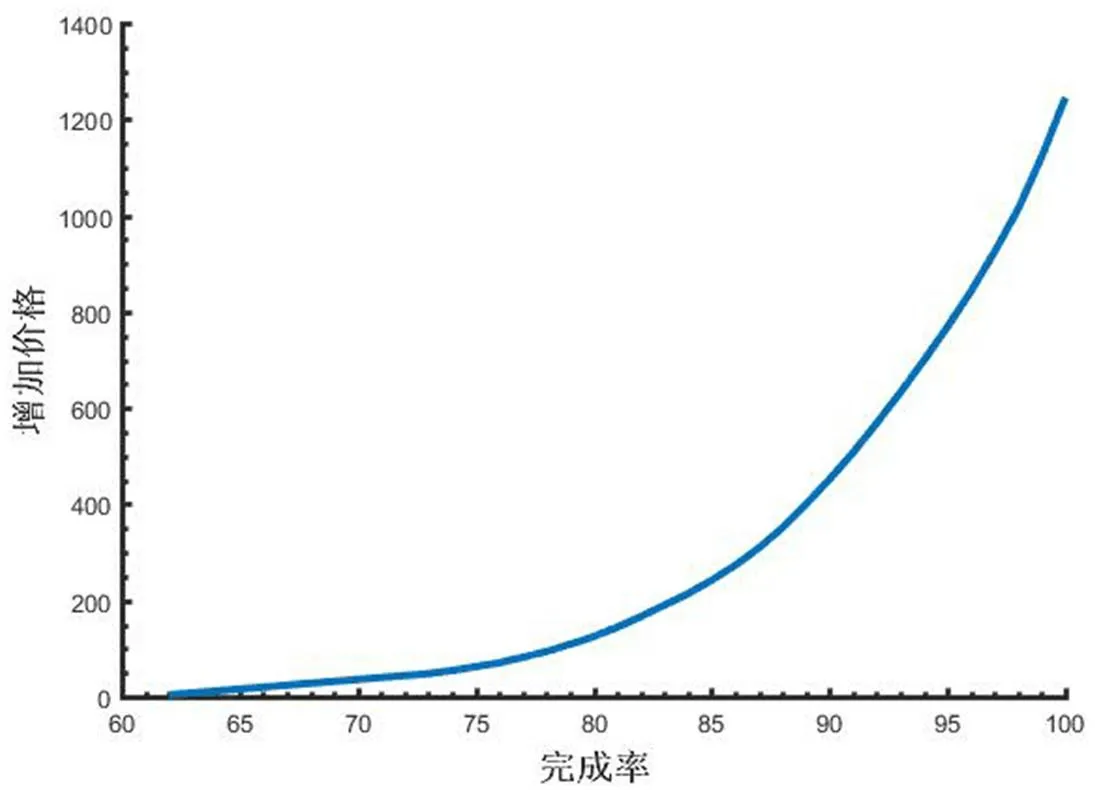
图3　任务价格增加量与任务完成率曲线图Fig.3　Diagram of task price increase and task completion rate

有序样本依次为 X1, X2,…,Xn，若某一类G包含样品有，则这一类的直径为

式中XG为类的均值向量

则分类法的损失函数为

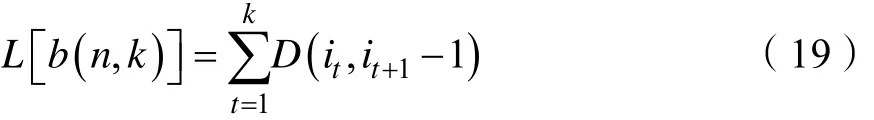
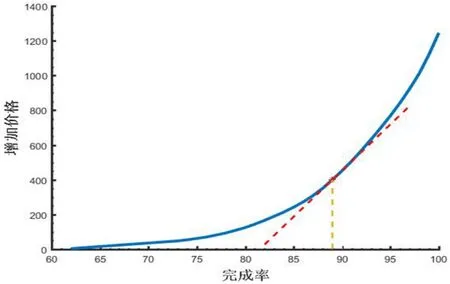
图4　最优分类点Fig.4　Optimal classification point

2.4　仿真结果

本文通过建立基于核函数的加权 KNN模型，迭代计算出所有情况下的任务价格，预测出相应任务价格下任务完成情况，根据增益梯度，采用有序样本聚类法找到完成率和相应增加价格的最优分割点，从而发现当增加的价格为400元时，任务完成率达到89%，并且得出各个任务的订单价格。

3　定价系统设计建议与改进方向

3.1　定价系统设计建议

· 不同类型众包平台具体量化而来的指标可能有显著差异，需要结合工作人员的经验，找出与任务完成情况有关的指标。建议以最近一段时间此地区的历史数据作为训练样本，确定当前阶段的最优定价方案。

· 特征工程是数据挖掘中最重要的一环，它决定了算法的上限，因此结合从业人员经验对任务各个指标进行选择、交互等操作可能会提高模型的实用性。

3.2　改进方向

·KNN类算法对于高维或者海量数据进行相似度量，计算时间会非常长，此时可以根据实际情况选择高性能计算，或者退而求其次采用随机森林算法、梯度提升树算法等进行接单判定，也能有较好的效果，同时节约计算成本。

4　结论

本文根据实例，对历史订单进行数据挖掘，揭示出隐藏在数据背后的灰色关系，合理地对任务完成情况进行仿真分类预测，同时根据平台自身发展情况构建多目标优化模型，提出了最优定价方案。综上所述，合理地构建了拍照赚钱的众包平台定价系统，同时易于迁移到各种众包平台对各种订单进行辅助定价。

未来可以进一步结合从业人员经验对特征处理，进一步提升模型适应性，处理海量数据时可以根据实际情况选择采用云计算或者更换效果较为接近的随机森林、梯度提升树等算法节约计算成本。