移动机器人养老服务路径规划的粒子群算法研究

陈曦斌，焦明海，刘昊汧，程亦然，张　浩

（1. 东北大学机械工程与自动化学院，辽宁 沈阳　110819；2. 东北大学计算机科学与工程学院，辽宁 沈阳　110819；3. 东北大学信息与工程学院，辽宁 沈阳　110819）

0　引言

随着经济社会的发展，中国人口老龄化规模越来越大，养老是中国未来社会发展的严重社会问题，也是一个重要的经济和政治问题。中国已经进入社会禀赋的深度，“老前富”和禀赋困境的现实显露出来。在当前的环境中，养老社区中的导向机器人的重要性是不言而喻的[1]。随着近年来人工智能技术的应用，中国政府作为工业和信息化部，发展和改革委员会，财政部联合发布了“机器人产业发展规划（2016-2020年）”[2]。根据该计划文件，机器人应用将在5年内投入服务行业。但事实上，中国老人导向机器人的研发并不理想。

机器人路径规划是根据给定的需求指令从起点到目标点选择一条路径，避开环境障碍物条件，并将位置从开始位置逐步移动到目标位置，以使机器人可以穿越所有障碍物安全和没有碰撞。这是移动机器人研究领域的热点问题[3]。移动机器人路径规划研究方便老年人社区护理服务。

移动机器人的路径规划可以根据机器人为路径感知而采取的工作空间环境信息划分为全局路径规划和局部路径规划。对于机器人移动路径规划优化，主要的传统路径规划算法是人工势场[4]，视觉反馈[5]和模块化可重构[6]方法。这些算法可以在不同程度上得到改进以获得良好的结果，但是这些算法具有其自身的限制。为了获得机器人规划的最优路径，人工智能算法[7,8]被应用于移动机器人的路径规划优化。研究成为人工智能解决移动机器人路径规划问题的热点问题。

对于人工智能算法的研究，群体智能算法是近年来机器人移动路径规划优化的热点。但移动机器人运动精度和全局路径规划的瓶颈问题也有待解决。自主无人机的发展是自动路径规划的能力。遗传算法（GA）和粒子群优化算法（PSO）相结合，以解决问题的复杂性和计算可行和准最佳轨迹[9]。文献[10]提出了在已知的静态粗糙地形环境下运行的类似汽车的移动机器人的路径规划算法，该算法找到了具有最小长度和地形粗糙度的无碰撞和可行路径。提出了基于二进制编码的静态和动态环境下移动机器人导航（MRN）二进制编码遗传算法的新变体，以轨迹理论为最优控制器，建立了SLI（Sylvester Law of Inertia）矩阵模型。另外还提出了另一种三层结构分层全局路径规划方法，用于移动机器人在杂乱环境中的应用。讨论了基于动态分布粒子群优化算法的最优路径规划算法，并考虑了使用两个局部最优检测器的无碰撞最优路径。并将人工蜂群算法作为局部搜索过程和进化规划算法相结合，对一组局部过程找到的可行路径进行优化。

1　养老机器人移动机器人路径规划优化问题

1.1　机器人工作空间的网格图模型

移动机器人可以帮助老年人在老年社区中完成引导、提醒、陪伴、安慰等生活事物工作。但移动机器人从起点移动到目标点时必须首先避开障碍物，机器人的工作空间可视化为网格图模型，如图1所示。

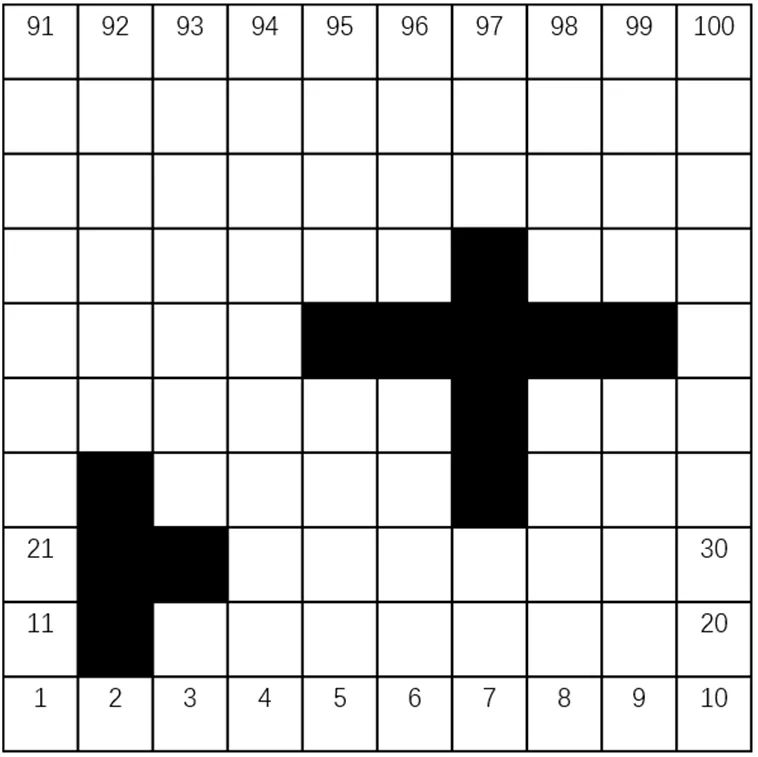
图1　移动机器人工作空间的网格图模型Fig.1　Grid graph model of working space of mobile robot

基于以下假设描述网格图模型：

a）机器人工作环境被定义为包括分类网格块的二维网格图;

b）在机器人工作环境中，分布着许多静态障碍物。障碍物的高度被忽略。每个障碍物可以在网格图中占据一个或多个网格块。

c）机器人被表示为没有质量或尺寸的粒子，称为粒子机器人。

d）粒子机器人每次移动一个网格步，当机器人从开始点移动到目标点时，网格移动步骤不能重复。

e）粒子机器人必须避开工作空间的障碍物。

图1显示移动机器人根据一百个网格块之一从起点移动到目标点。二维网格图空间被标记为从左侧块到右侧块的排序号码，从底部到上一块，从1到100排序。灰色网格块是粒子机器人避免移动的障碍。

定义1移动机器人工作空间被描述为一个二维地图，它被划分为行网格块和列网格块。网格块的数量描述如下。

参数R是机器人移动每个步长的大小。Nx和Ny分别是工作空间图的长度和宽度。Xmax和Ymax分别是最大长度和最大宽度。R，Xmax，Ymax的参数设置为1,10,10。因此，10*10尺寸的机器人工作空间图被划分为100个网格块尺寸。排序后的数字在图1中标出。

1.2　路径规划优化模型

机器人路径规划优化的目标不仅是寻找机器人从网格图中的起点到目标点的最短路径，而且还避免与障碍物块的碰撞。移动机器人路径规划的研究被认为是一个约束优化问题。并建立了优化目标函数和约束条件的路径规划优化模型。优化目标为最小路径代价，约束条件有效避免路径规划中的障碍。

为了解决优化问题，约束条件被转化为优化目标函数，其被定义为最小冲突惩罚函数。然后给出该模型作为两个优化目标函数，其中包括最小路径成本和最小碰撞惩罚。对老年服务而言，老年社区的障碍问题对老年人来说是一段非常危险的时期，这些障碍包括水泥墙，带刺植物躯干，台阶等等。因此碰撞处罚也被定义为碰撞系数，表示移动机器人应远离障碍物的危险等级。

移动机器人在网格图中移动的路径规划优化模型如下：

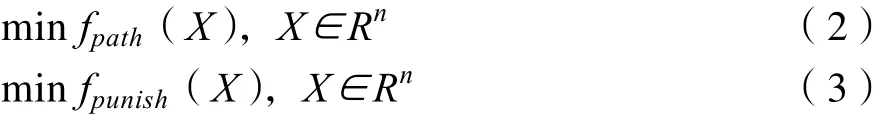
优化函数 fpath是包含网格图中机器人每走一步的路径的总距离。如下所示：

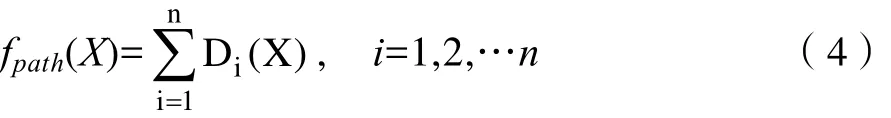
Di是机器人第 i步的路径距离，其被描述为每个网格长度，并且n是网格块的总数。优化函数fpunish定义如下：

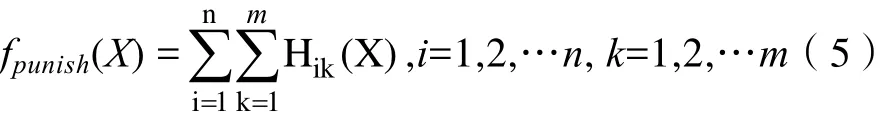
Hik是由机器人步进网格块i碰撞的障碍块k的惩罚系数。参数n是网格块的总数，m是障碍块的总数。考虑到求解问题的一致性，将多目标优化模型合并为单目标优化问题。如下所示：

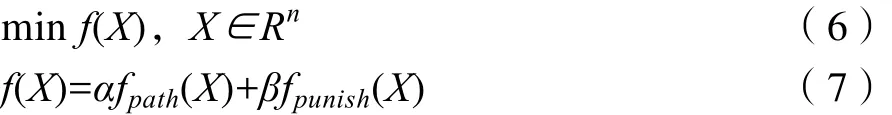
粒子群优化算法有效解决了单一优化问题，参数α和β是经验系数，满足α+β= 1。

1.3　人工势场法

采用人工势场法进行路径探测，避开障碍物，根据目标点包含引力场和排斥场。在虚拟势场中，机器人移动点与目标点之间的距离越大，势能越大。距离目标点越近，势能越小，到达目标点时势能为零。机器人移动点与障碍物之间的距离越近，排斥力越大。

引力势场函数定义如下：

Ugra是引力势场函数。k是重力场常数参数，其值大于零。X是当前机器人位置点向量。而Xg是目标位置矢量。

排斥势场函数定义如下：

Urep是排斥势场函数。λ是一个排斥场常数参数，其值大于零。参数ρ是机器人位置与障碍物之间的距离。ρ0是障碍物的最大影响范围。机器人在吸引和排斥方面互动，向前移动到目标点。

2　解决路径规划问题的粒子群优化算法

2.1　粒子群优化算法

粒子群优化算法是人工智能搜索思想的有效解决方法。粒子在目标搜索空间寻找最优解。粒子群优化算法表述为：假设搜索空间为d维，种群中有Np个粒，那么群体中的粒子 i在第 t代的位置表示为一个d维矢量。粒子的速度定义为位置的改变，用矢量 V表示。粒子i的速度和位置更新公式为：

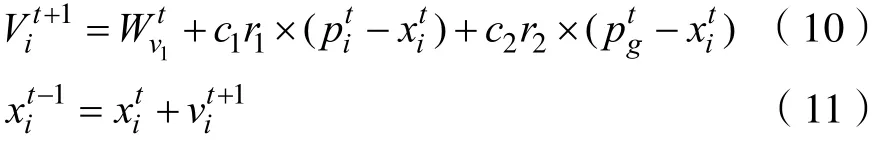
式中，t为粒子更新迭代次数。在第t代，粒子i在 d维空间中所经历过的“最好”位置记作；粒子群中“最好”的粒子位置为惯性系数；cl和 c2为加速系数；r1和r2为区间[0, l]服从均匀分布的两个独立随机数。参数w、cl、c2的取值依赖于问题。

2.2　编码和解码方法

a）粒子编码：网格图大小是解空间，如图1中的10*10大小。从左到右，然后从下到上，排序后的数在每个网格块中标记为索引。因此每个粒子都有一个选定的m维解。考虑障碍块是无意义的解决方案，真正的解决方案大小是m = Dtotal-Dobstacle，Dtotal是总的网格块大小，Dobstacle是障碍网格块大小。粒子编码的问题是如何为移动移动步骤选择网格块。作为粒子编码方法的新思想是给每个有效网格块的概率为xij（j = 1,2,…,m）变量。根据网格图大小将概率范围设置为灵活变量值，并且不一定是0和1的区间。

b）粒子解码：对于编码方法来说是相反的，其重点在于根据给定的更新概率选择最优网格块作为移动机器人移动步骤。粒子解码的重要主题是网格块选择。从网格图中，如图1所示，每个网格块具有不同的相邻网格块，因此可选的相邻网格块在网格图中定义。例如，图1中左下方的网格块是移动机器人移动步骤的起点，标记为数字“1”。然后，起点的相邻网格块应该是三个可选的网格块，标记为数字‘2’，‘11’，‘12’。经过优化迭代过程后，起始位置的邻居网格块具有各自的概率值，最大邻居块被选为移动机器人的移动步骤。对于粒子解码解决方案，屏障网格块将被忽略。并且自由网格块具有最大八个相邻网格块，诸如具有标记为数字“4”，“5”，“6”，“14”，“16”，“24”的相邻网格块的空闲块编号“15”，“25”，“26”。对于网格图的移动路径，该块不被重复选择。

3　实验和性能分析

3.1　实验设计

实验平台是专为硬件和软件环境而设计的。 硬件是老年服务移动机器人的原型，它可以沿着室内和老年社区的优化路径随着三个轮子移动。 该软件是具有路径规划管理和决策系统的控制模块。

该实验仅针对粒子优化算法求解的网格图模式而设计。模型的细节设置如下。

表1　模型设置Tab.1　Model setting

该算法在 windows操作系统或 linux操作系统上实现。 上述系统的实验描述如下：CPU为Core i5 3.3 GHz，内存大小为8 G，仿真环境为Visual C++。

3.2　实验结果

考虑避免碰撞的最佳移动机器人移动路径如图2所示。

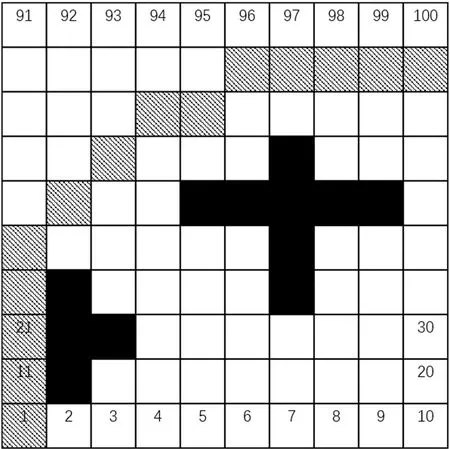
图2　最佳移动机器人移动路径Fig.2　The best mobile moving path of mobile robot

所有移动步骤都组成移动机器人路径。考虑避免碰撞的最佳路径是一种折中结果，其不仅包括最短路径优化，而且还避免了危险障碍。老年人社区中的机器人是一种重要的辅助手段，可以帮助老年人缓慢行走，避开危险物体。因此，尽管是最短的优化路径，但与障碍块侧面接触一样，不满足最佳路径决策。

当目标位置发生变化时，粒子群优化算法也被有效地应用于求解所提出的网格图模型。例如，当目标位置被改变为索引号69的网格块时，该算法被实施以根据所存储的全局路径规划来选择最佳 路径。

3.3　实验性能分析

实验针对移动机器人运动路径问题求解，提出粒子群优化算法（PSO），蚁群算法（AC）和遗传算法（GA）的性能对比。运行时间不同优化算法的实验结果如表2所示。

从网格图模型优化中的路径规划实验结果来看，粒子群算法克服了其他有效的人工智能算法。

该算法也可以在算法运行过程中执行相同的迭代次数。这三种算法在相同的标准实验环境下进行1000次迭代运行。

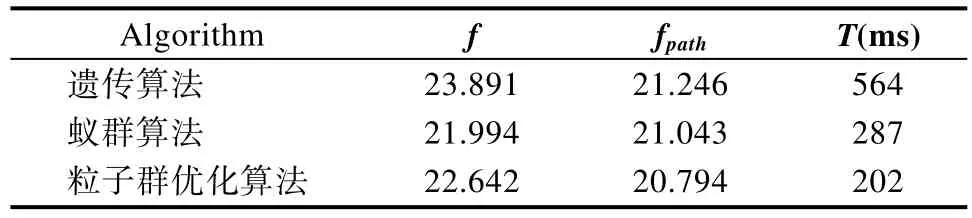
表2　算法的优化结果Tab.2　Optimized results of algorithm

4　结论

老年群体中移动导向机器人的路径规划问题是一个多重障碍和约束的复杂优化问题。为了更好地满足老年人的导游路径要求，如何选择最短路径和无碰撞成为提出路径规划问题的最重要的解决方案。提出了移动机器人运动路径规划模型，用于辅助老年人走出房间，走出房间引导。还提出了粒子群优化算法来解决路径规划问题。该模型被定义为10*10大小的网格图，包括两个障碍物。并提出了人工势场法来加速路径优化过程。该实验旨在验证所提出的求解算法的性能。结果表明，粒子群优化算法对老年社区老年服务移动机器人移动路径规划问题是有效和高效的。