基于Boxplot-LTSA噪声流形算法的滚动轴承状态识别*

刘忠鑫，康建设，曲凤明，邓雅冲

（1.陆军工程大学石家庄校区，石家庄 050003；2.解放军63856部队，吉林 白城 100037；3.陆军装甲兵军事代表局驻天津地区军代室，天津 300161）

0 引言

自从 2000年，Seung［1-3］等人发表了 3篇流形学习开创性的研究成果，流形学习越来越多地被用到了数据处理中，与传统的线性判别分析、主成分分析方法、核主成分分析方法相比，流形学习对非全局线性、高维数据的可视化具有很大优势，能够从海量的数据中寻找到数据中蕴含的内部几何结构及其规律。郝腾飞［4］将流形学习中的拉普拉斯算法应用到旋转机械的特征提取中，显著提高了故障诊断的正确率；肖婷［5］等人利用流形学习和最小二乘支持向量机的方法对滚动轴承进行退化趋势预测；何青［6］等人基于流形学习方法对汽轮机组进行特征提取，取得良好的效果。但是在实际应用中发现，几乎任何一种流形学习算法都存在对噪声数据比较敏感，要求稠密均匀取样以及泛化能力差等缺点，造成了流形学习在实际应用中还存在一定的问题，针对此，国内外专家学者做了大量研究。国防科学技术大学的詹宇斌［7］提出了一种噪声健壮的流形学习算法；Choi［8］等成功地将Mercer核引入ISOMAP算法中，提高了原算法的泛化学习能力，同时其算法对抑制噪声干扰有良好效果；Chang［9］等提出了一种鲁棒局部线性嵌入算法（RLLE）来消除原始的局部线性嵌入算法对噪声敏感，取得良好的效果。

本文主要针对滚动轴承采集到的信号往往受到噪声干扰，利用Boxplot算法对原始信号进行去噪声处理，再利用局部切空间排列方法（LTSA）对处理后的信号进行降维，达到可视化的目的，并通过与直接使用流形学习算法降维结果进行比较，表明该算法对于受到噪声干扰的滚动轴承信号有着良好的故障诊断效果。

1 Boxplot-LTSA算法

1.1 Boxplot算法基本原理

Boxplot箱线图实质上是使用统计的方法对每一个点进行识别，Boxplot算法在实现过程中的关键是求出每一点的权值向量，利用权值向量进行判断。分别对奇异值上下限进行定义，上限定义为{Q1+α（Q3-Q1）}，下限定义为{Q1-α（Q3-Q1）}，其中，α∈［1.0，1.5］当数据点的权值超出上下限，认为就是被噪声污染的点，通过调节α具体确定上下限，与以往统计方法数据去噪相比，Boxplot箱线图在进行噪声识别时，不需要假设数据服从正态分布，具有很好的适用性，一般认为使用统计方法识别噪声点，噪声点个数不能超过1%，但Boxplot箱线图最多能够容忍25%的数据点被噪声污染，在计算复杂程度上，Boxplot箱线图方法计算简便快捷，能够满足超大数据量的运算要求。

1.2 Boxplot算法实现过程

Boxplot算法是通过计算每一点的权值向量来实现的。具体过程为：

2）利用主成分分析方法，计算原始高维矩阵的低维映射X'，以及反映射变换回来的像X''，因为经过主成分后的反映射与原始高维矩阵之间会产生一个误差，记为 εj，εj=X'-X''。

4） 输出权值向量 W=［w1，w2，…，wn］。

利用权值向量，采用Boxplot箱线图算法识别其中的奇异值，认为奇异值在原始矩阵中的对应点被噪声污染，予以删除，获取经过处理的矩阵Ti。

采用局部线性嵌入算法对高维矩阵进行降维处理，获得低维映射矩阵

1.3 局部切空间排列算法（LTSA）

局部切空间排列算法（LTSA）是一种针对样本存在孔洞情况下的有效的流行学习算法，同时计算量小，执行速度快。其算法步骤为：

Dijb表示第i类和第j类之间的类间距向量；Diw表示第j类的类内距向量；n为类别数。

2）计算局部切空间坐标，对XNi进行中心化处理，求得进行奇异值分解，得到左右奇异向量所构成的矩阵Qi、Vi，选取最大的d个奇异值对应的右奇异向量，组建矩阵Vi'；同时得到的最优解，即：，构建出局部坐标系

3）局部坐标全局排列

将这些有交叠的局部坐标系统Θi排列起来得到全局坐标系统 T，T=［Ti，…，TN］。Θi经过局部排列矩阵Li（待确定）仿射转换全局坐标为：Ti=［ti1，ti2，…，tik］，则局部重构误差为：，为了尽可能保持局部低维特征，极小化重建误差，即：，固定全局坐标矩阵Ti，最小化局部重构误差矩阵Ei，重建误差又可以写成：，其中为排列矩阵，是满足的选择矩阵，I是单位阵，，这样通过计算φ的第2到第d+1小的特征值所对应的特征向量就可以获得低维映射，即 T=［u2，…，ud+1］。

2 Boxplot-LTSA算法实现过程

本文采用Boxplot-LTSA算法进行滚动轴承状态识别，直接对去噪后的原始振动信号进行处理，减少了在时频域特征提取中造成的信息失真，增强了可视化的准确性。

2.1 原始状态矩阵构建

通过Boxplot算法对原始数据各个不同状态进行噪声识别，去噪后的新数据集为Ti（i=1，2，…，n），将Ti均匀分成l组建立原始状态矩阵XiM×l，对矩阵X使用LTSA算法进行维数约减，达到滚动轴承状态识别的目的。

2.2 关键参数的确定

嵌入维数的确定：在进行维数约减，实现可视化过程中，根据文献［10-11］的研究结果，最优的嵌入维数d为故障类数减去1，即d=n-1。

本研究提出以原始振动信号建立高维矩阵，以原始信号构建高维矩阵时l值的确定十分重要：在信号点数量一定的情况下，l较小时不同状态的聚类效果很好，但是各个不同故障低维映射重叠严重，无法分辨轴承故障状态；当l较大时，可以通过低维映射识别不同故障，但是同类故障的聚类效果不好，误判率较高，无法实现准确的状态识别。本文中分别使l=10，50，100，500，1 000，2 000，寻找合适的 l值。

3 应用实例

3.1 应用对象

本文以滚动轴承作为研究对象，选择美国凯斯西储大学（Case Western Reserve University）电气工程实验室的滚动轴承，该数据来源于SKF6205滚动轴承，其采样频率为12 kHz，预置故障的损伤尺寸为0.355 6 mm，分别选取该条件下的内环故障、外环故障、滚动体故障以及正常情况下的实验数据，构建原始矩阵。

3.2 对比分析

为了验证本研究的有效性，通过与直接使用流形学习算法降维处理结果比较验证。

3.2.1 原始数据去噪处理

利用IRLS算法，计算每个点的权值，利用箱线图找出奇异值，在原始矩阵中去除被噪声污染的点，组建新的原始矩阵。如图 1（a）～ 图 1（d）所示，分别为内环故障、外圈故障、滚动体故障以及健康状态下的奇异值识别结果，图中红色“+”代表奇异值，不难看出，健康状态下原始数据中受噪声污染的数据点最少，符合实际预期。分别找出原始矩阵中对应值，删除后得到去噪后的原始矩阵X。

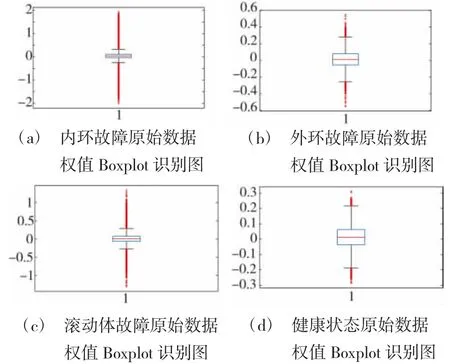
图1 新的原始矩阵

3.2.2 基于去噪流形学习算法的三维可视化

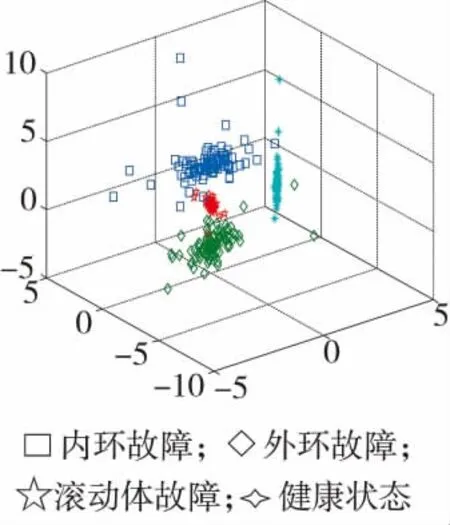
图2 l=1 000时Boxplot-LTSA降维映射分布图

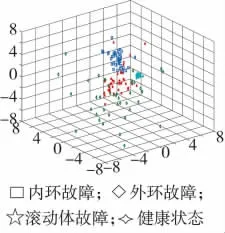
图3 l=2 000时Boxplot-LTSA降维映射分布图

将新的原始矩阵利用LTSA算法进行降维，近邻点数量k=l/2，嵌入维数d=3。分别选择l=10，50，100，500，1 000，2 000，由于篇幅原因，给出部分l值时低维映射结果。其中当l=1 000时，如图2所示，在三维坐标系中，不同故障的低维映射坐标有明显的区别，可以实现不同故障类型的诊断。当l=2 000时，如图3所示，健康状态下的低维映射聚类很好，内环故障和滚动体故障聚类效果一般，在进行故障识别时会出现一定的误判，外环故障聚类最差，无法完成故障识别。当l=500时，如图4所示，健康状态下的低维映射聚类很好，且与其他3种状态无重叠，可以实现故障识别，内环故障、滚动体故障、外环故障的低维映射尽管聚类很好，但是却重叠严重，无法准确判断故障位置。当l=10，50，100时，低维映射结果没有明显区别，不同状态的三维映射重叠十分严重，无法区分不同故障类型。最终经过测试l∈（900，1 200）时，可以达到分类要求。

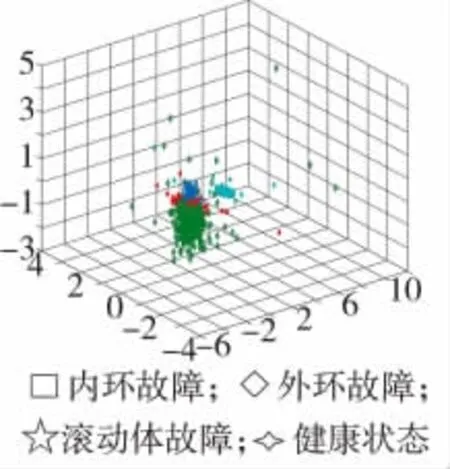
图4 l=500时Boxplot-LTSA降维映射分布图

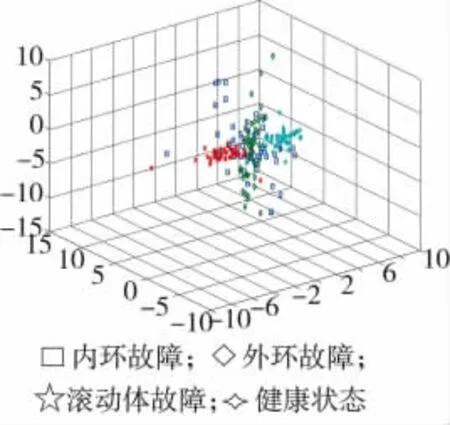
图5 l=1 000时LTSA降维映射分布图

3.3 基于不去噪流形学习算法的三维可视化

将不经Boxplot算法处理的数据，直接进行维数约减，选择近邻点 k=l/2，嵌入维数 d=3，l=1 000，其三维图如图5所示，健康状态、滚动体故障的低维映射聚类效果较好，但是内环故障、外环故障振动信号明显受到了干扰，并且，不同故障类型的低维映射重叠严重，很难通过降维识别出故障位置。因此，噪声、冲击等干扰对原始信号的影响确实是存在的，破坏了原始信号的内部流形结构，因此，在不经去噪处理的情况下，利用流形学习进行维数约减无法找出其内在规律。

3.4 验证与分析

为了进一步验证该方法的有效性，分别选取4种状态下的训练数据，组建M×l矩阵，其中l=1 000，k=l/2，利用Boxplot-LTSA算法进行降维处理，通过低维映射，内环故障、外环故障、滚动体故障、健康状态的识别率分别达到了97.5%、95%、96.2%、99%。

LTSA流形学习算法对噪声信号的鲁棒性较差，且对样本点的密度和曲率变化敏感，样本点密度和曲率的变化会使得样本点到流形局部切空间的投影产生偏差。在消噪过程中，不可避免地一部分干净信号被去除，一部分噪声信号被留下，经过探索，当 l∈（900，1 200）时，剩余噪声信号在每个维度的分割相对均匀，且信噪比也较低，噪声影响降到了可以接受的程度，因此，能够达到较好的映射效果，实现了滚动轴承的故障诊断。

4 结论

本文以滚动轴承为背景，针对传感器采集到的数据易受到噪声、振动、冲击等多因素影响，提出了一种基于Boxplot-LTSA的噪声流形学习算法，Boxplot算法对噪声信号的耐抗性与LTSA算法在数据存在孔洞情况下良好的鲁棒性结合，获取的低维映射很好地反映了滚动轴承不同故障信息，达到了状态识别的目的。