多等级供应模式下鱼雷武器备件补给策略优化*

魏 勇 ，邵松世 ，原 龙 ，侯聚林

（1.海军潜艇学院，山东 青岛 266199；2.海军工程大学科研部，武汉 430033；3.解放军91352部队，山东 威海 264200）

0 引言

在多等级保障组织体系里，备件处于不同等级的保障单位时，发挥的作用也不同。在过去几十年中出现了大量备件预测相关模型及方法，如以METRIC 和 VARI-METRIC 为代表的采用（S-1，S）补给策略的多等级库存系统预测模型［1］；Muckstadt［2］将备件结构层级进行分解，提出了多层级MODE-METRIC 模型；Graves［3］研究了该模型近似算法的简单推导过程并通过试验对其进行验证；Slay和Sherbrooke提出了备件初始配置优化的多等级多层级理论，即VARI-METRIC模型［4］。综观这些模型，其理论最初瞄准的是高可靠性或贵重件的备件供应问题。因为贵重，所以有其最终修复概率等于1的假定［5］。因为高可靠性，所以故障率低、故障间隔时间长。所以从高可靠性、贵重件的备件库存角度，采用（S-1，S）策略无疑是合理的［6］。

但是在装备中，除了高可靠性、贵重的部件外，还有那些可靠性和价格都一般的部件。对这些部件，无论是理论上还是实际工作中，如果仍然采用“消耗一件、申请一件、补充一件”的（S-1，S）策略，则不尽合理，需要对其他备件补给策略进行研究。

因此，本文针对那些可靠性和价格都一般的部件，在多级供应模式下［7］，当站点发生一次故障、消耗一件备件后，不急于马上申请备件，而是依靠站点当前的剩余备件数量时，提出采用（S-X，S）补给策略，在此基础上利用Gamma等效评估法，建立备件保障效果使用可用度数学模型，对不完全修复件进行各站点备件方案的保障效果评估，为解决该类装备的备件配置供应问题提供了通用的方法。

1 问题描述

所谓（S-X，S）策略，在本文中指：每当站点发生一次故障、消耗一件备件后，不急于马上申请备件，而是依靠站点当前的剩余备件数量，评估在剩余任务时间内完成任务的可能性，计算其能否满足执行任务期间的保障要求。如果不能达到保障要求，再发出备件补充申请。在（S-X，S）策略中，X指站点备件累计消耗的数量，当剩余备件数量S-X不能满足剩余任务时间的保障要求时，才请求补充备件。X的物理含义是备件补给时机。显然，在（S-X，S）策略下，站点会优先、充分使用自身的备件，只有当觉得无把握达到保障要求时，才会发出备件申请，“消耗”后方仓库的备件。

无论是（S-1，S）策略还是（S-X，S）策略，其描述的是站点与上级保障机构之间关于备件补充的约定，与装备内的层级结构无关。因此，本文中，以单层装备、两级保障组织结构、多站点（站点上的装备列装数量各不相同）为背景，进行论述，如图1所示。

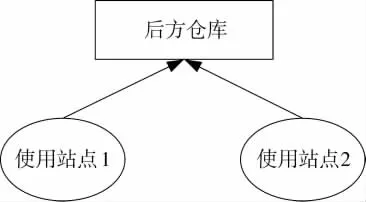
图1 两级保障组织体系结构图

对于（S-1，S）策略，当站点的装备发生故障后，将随之发生以下事件：

1）在站点，使用备件对故障件进行换件维修以排除故障、装备恢复工作。

2）在站点，对故障件进行修理，如果修理失败，则故障件送往上级保障机构继续修理。

3）当站点的故障件修理失败后，向上级保障机构申请一件备件，用于补充站点消耗的备件。

对于（S-X，S）策略，当站点的装备发生故障后，将随之发生以下事件：

1）在站点，使用备件对故障件进行换件维修以排除故障、装备恢复工作。

2）在站点，对故障件进行修理，如果修理失败，则故障件送往上级保障机构继续修理。

3）站点每发生一次故障，根据站点现有备件数量，计算其在剩余任务时间内的保障效果，并与保障要求Pa0相比较，如果低于保障要求则向后方仓库申领一件备件。

比较上述故障发生后的事件处理过程，发现在更换故障件和修理故障件上，无论采用（S-1，S）或（S-X，S）策略，二者其实并无区别，并没有因为补给策略发生变化而变化。受补给策略变化影响的，只是备件申请时机和备件补充数量。

因此，采用（S-X，S）策略的保障过程仿真模型，其流程其实与采用（S-1，S）策略的仿真模型大体一样，只需在（S-X，S）策略的仿真模型基础上，改变站点的备件申请和后方仓库的申请响应部分，就可以实现（S-X，S）策略下的保障过程仿真。

2 使用可用度数学模型

2.1 问题假设

记保障任务时间为Tw，假定：1）保障组织体系为两级两站点，后方仓库备件数量记为S1，站点1自身配备的备件数量记为S21，站点2自身配备的备件数量记为S22。2）站点1配有n1个产品单元，站点2配有n2个产品单元；产品单元为不修复件，寿命服从指数分布exp（μ）；站点内各单元之间为串联关系；各个站点的产品为连续工作，每天的工作时间相同。3）站点向后方仓库提出备件申请的耗时为零。4）备件从后方仓库到站点存在运输时间Ty12，Ty12为常数，其物理含义为平均运输时间。5）在站点，该产品单元（不修复件）发生故障后即报废，通过用备件更换故障件的方式使产品单元恢复工作，换件维修耗时为零。6）站点采用（S-1，S）备件补给策略时：站点每发生一次故障，向后方仓库申领一件备件。7）站点采用（S-X，S）备件补给策略时：站点每发生一次故障，根据站点现有备件数量，计算其在剩余任务时间内的保障效果，并与保障要求Pa0相比较，如果低于保障要求则向后方仓库申领一件备件。

分别采用（S-1，S）和（S-X，S）备件补给策略，建立仿真模型，模拟备件方案的保障效果，统计各个站点备件方案的使用可用度。

2.2 （S-1，S）策略使用可用度统计模型

2.2.1 备件数量比例模型

以两级两站点为例，某型产品单元在站点1的列装数量为n1，在站点2的列装数量为n2，假定该产品在两个站点的每天工作时间相同，则对于寿命服从指数分布exp（μ）的单元，由于指数分布的无记忆性，其在某时间区间段内发生故障的次数与区间的时间起点/终点无关，只与区间的长度t有关，且该时间内的平均故障次数为：

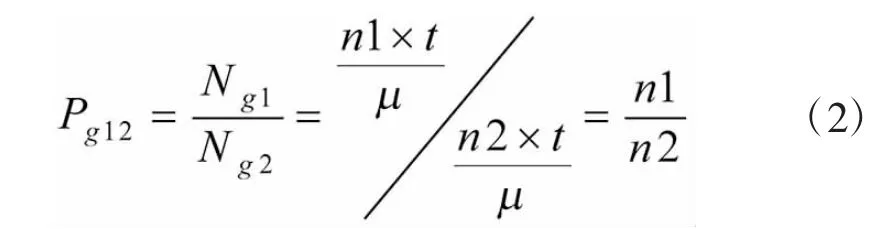
因此，站点1竞争到的上级备件数量占上级总备件数量的比例Pg1为：

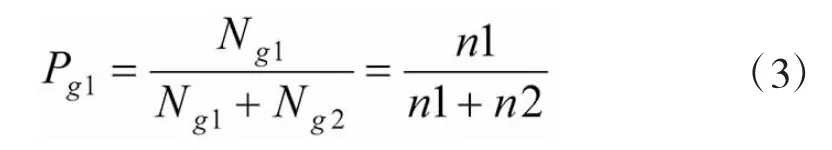
站点2竞争到的上级备件数量占上级总备件数量的比例Pg2为：

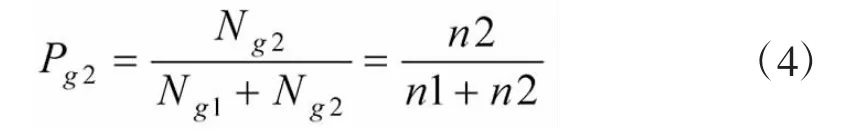
2.2.2 使用可用度模型

1）产品单元的故障间隔时间服从指数分布exp（μ），则等效后的不修复件寿命服从指数分布exp（μ2）。

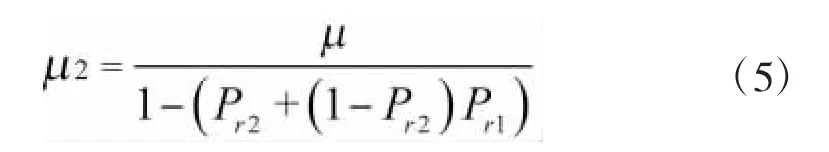
2）站点1、站点2获得后方仓库备件数量S11、S12为：

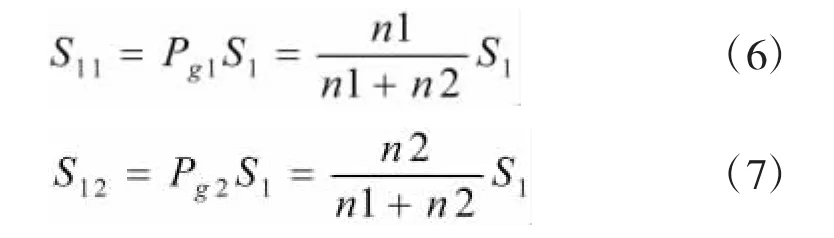
3）根据Gamma分布的卷积特性，S1在批次备件支持下，站点1该部件的累积工作时间服从Gamma分布Ga（1+S11+S21，μ2/n1），站点2该部件的累积工作时间服从Gamma分布Ga（1+S12+S22，μ2/n2）。

则备件保障概率P1就是Ga（1+S11+S21，μ2/n1）分布的可靠度R1（Tw），因此：

备件保障概率P2就是Ga（1+S12+S22，μ2/n2）分布的可靠度R2（Tw），因此：

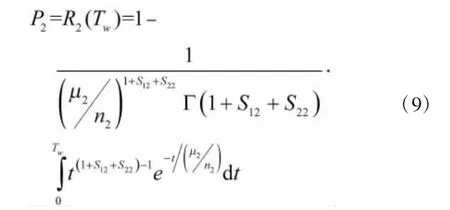
在Matlab中，利用计算Gamma分布的失效度函数gamcdf（），上述两式可表达为

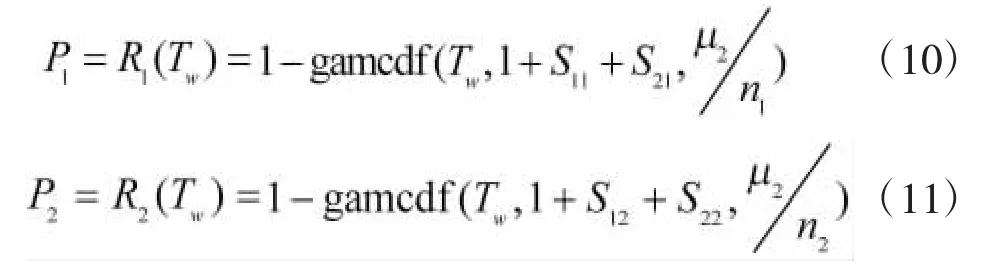
由于使用可用度是平均保障概率，因此，两产品在保障任务期间的使用可用度AO为：

2.3 （S-X，S）策略使用可用度统计模型

该统计模型基于离散事件仿真原理实现，模型中的关键事件为发生故障。在现实中，故障发生后的业务主要有2项：

1）备件申请/响应。根据（S-X，S）备件补给策略，站点向后方仓库请求补给一批备件。如果后方仓库视备件库存情况，尽快向站点下拨备件，该备件发出后，经运输时间Ty后到达站点。

2）换件维修。在装备现场，如果站点有备件，则立刻开展换件维修；如果站点没有备件则视1）备件申请结果而决定—如果后方仓库有备件，则在Ty后备件到达时，完成换件维修，装备继续工作；如果后方仓库始终没有备件，则装备永久停机，保障任务失败。

由于换件维修的结果有赖于申请备件事件的结果，为了更好地仿真实现上述故障处理业务，对站点中的第i件备件建立一个包含2项数值的行数组来表达，行数组的结构如下：

sTi为该备件最早在站点能被用于换件维修的时间。

sFi为该备件是否已被消耗，未消耗时：

令sFi=1，已消耗令sFi=0。

仿真流程如下：

1）仿真初始化。仿真时间simT=0，站点1和站点2的备件仓库可用如下矩阵wareS21、wareS22表示：

2）模拟故障。根据产品单元的故障间隔时间统计规律产生随机数Trnd，令simT=simT+Trnd，simT为模拟的故障发生时刻。

3）模拟备件申请/响应。在故障发生时刻simT，首先模拟后方仓库对站点的备件申请响应如下：

判断S1是否大于X。

是，则在站点备件矩阵的最后增加一条行数据。

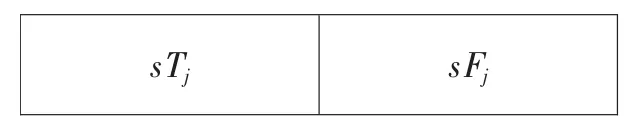
且sTj=simT+Ty、sFj=X，更新后方仓库的库存状态：S1=S1-X。

4）模拟站点的换件维修。先在wareS21、wareS22中找出所有未被消耗的可用备件，再在可用备件中找出能被最先使用（sTj中最小）的备件，其序号记为k，更新站点备件库存信息：令sFk=0。则sFk和simT中的最大值为换件维修完毕、故障排除装备开始继续工作的时刻，推进仿真时间到该时刻：simT=max（sTk，simT）。

5）判断仿真是否终止。

如果不满足终止条件，则转式（2）。

仿真终止条件为满足以下两个条件中的任意一个：

条件1：simT大于等于Tw；

条件2：站点备件仓库wareS21、wareS22中找不到可用备件。

在仿真终止后，统计各站点产品的累积工作时间simTw，利用累积工作时间可计算各站点使用可用度：

3 算例分析

算例参数：假定某鱼雷武器保障任务时间Tw的取值范围为3 000～10 000，备件仓库备件数量S1=6；站点1的列装数n1=1，备件数量S21=2；站点2的列装数n2=3，备件数量S22=10；产品单元平均寿命μ=1 000，备件运输时间Ty12=100，保障要求Pa0=0.9。

对上述参数进行分析，发现：如果不考虑后方仓库的备件，站点1的初始备件方案是一个即便保障任务时间Tw=2 000，备件数量仍显不足的“坏”方案（其使用可用度为0.730）；站点2的初始备件方案是一个保障任务时间长达Tw=4 000，其使用可用度仍可高达0.915的备件数量较为充足的“好”方案。

图2显示了不同备件补给策略对站点方案保障效果的影响。

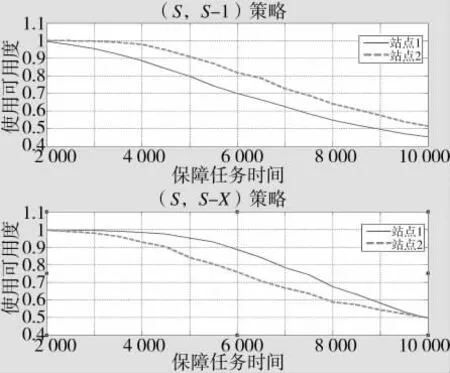
图2 两种备件补给策略对不同站点使用可用度的影响结果

从图2可以看出：

1）采用（S-1，S）备件补给策略时，由于站点2的列装数量大于站点1，因此，后方仓库的备件大部分会分配给站点2，站点1和站点2由于初始方案导致的“坏、好”差异虽然由于后方仓库备件的原因有所改善，但站点1和站点2同时满足使用可用度不低于0.9保障要求的保障任务时间小于4 000。

2）采用（S-X，S）备件补给策略时，由于站点 1备件方案的“先天不足”和站点2备件数量较为充分，站点1会优先提出备件申请，因此，站点1的保障效果得到明显改善，站点1和站点2同时满足使用可用度不低于0.9保障要求的保障任务时间可以达到4 500。

图3显示了各站点备件方案受不同备件补给策略的保障效果影响情况。

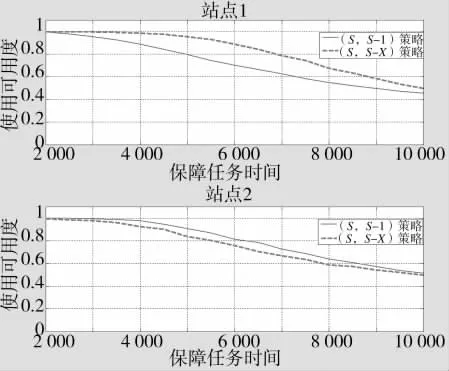
图3 各站点使用可用度受两种备件补给策略的影响结果

从图3可以看出：

1）站点 1受益于（S-X，S）备件补给策略，能有效改善保障效果。

2）在保障任务时间较短或较长的情况下，站点2在（S-1，S）和（S-X，S）备件补给策略下的保障结果差别不大。只有在使用可用度为中等数值情况下，站点2在（S-X，S）备件补给策略下的保障结果会稍逊于（S-1，S）备件补给策略，其原因在于该算例中后方仓库的初始备件数量有限，站点1的备件申请更为“急迫”、先期被满足，后期可分配的后方仓库备件数量相对减少，导致使用可用度有所减少。

4 结论

显然，在（S-X，S）策略下，站点会优先、充分使用自身的备件，只有当觉得无把握达到保障要求时，才会发出备件申请，“消耗”后方仓库的备件。此时，后方仓库备件的作用可以称之为“雪中送炭”。相比（S-1，S）策略，（S-X，S）策略有可能更为显著地发挥上级保障单位“扶危济困”的作用。