坦克炮控系统神经网络自适应滑模控制方法

胡继辉，侯远龙，高 强，陈宇政，童仲志

（南京理工大学机械工程学院，南京 210094）

0 引言

全电式坦克炮是一种复杂的炮控伺服系统，其内部存在强本质非线性环节［1］。影响该系统的主要非线性因素有：传动装置存在的间隙，耳轴和炮管之间的摩擦以及身管质心和耳轴轴心不重合造成的非平衡力矩［2-5］。此外由于测量误差不可避免，系统的某些参数具有明显不确定性。而现如今坦克炮控系统大多被简化为线性定常系统［6］，在此基础上对其进行建模，并采用经典控制理论对其进行控制。因此，对上述非线性和时变性不能很好地补偿，控制效果也达不到预期。

滑模变结构控制对系统未建模动态具有很强的鲁棒性，对外部干扰和系统参数摄动具有不变性，因此，在非线性系统控制方面具有很大的优越性［7］。但由于滑模变结构控制的不连续开关特性，在滑模面上不可避免地产生抖振，影响系统的动静态性能，使系统产生超调；且抖振会加剧坦克炮控系统中的机械磨损，增大系统的能耗，甚至可能会引起固有振荡，影响控制系统的正常工作。RBF神经网络滑模变结构控制将RBF神经网络逼近功能和滑模变结构控制结合起来，既保证系统对参数摄动和外部干扰较强的鲁棒性，又能够使控制信号柔化，尽量削弱系统抖振。

文献［8］研究单纯的滑模变结构控制方法，文献［9］将模糊规则和滑膜变结构控制相结合。都取得不错的效果，但简单滑模控制系统会存在抖振，模糊滑模控制实现的算法较为复杂。本文以坦克炮的高低向伺服系统为研究对象，对其进行建模，并对RBF神经网络滑模变结构控制律进行理论设计和数值仿真。本文提出的控制方案为坦克炮控系统非线性补偿提供了一种理想的解决方案，且实现算法较为简单，取得了良好的控制效果。

1 坦克炮控系统结构与建模

1.1 坦克炮控系统结构

坦克炮控系统是一种典型的伺服系统，由高低向和水平向伺服系统组成。按传动方式可分为电液传动式和全电式，电液传动式是传统的炮控系统，而全电式炮控系统是当今主流的发展方向。全电式是指采用执行电机作为系统的执行机构［10］。本文对全电式坦克炮高低向分系统进行分析研究，其结构框图如图1所示。

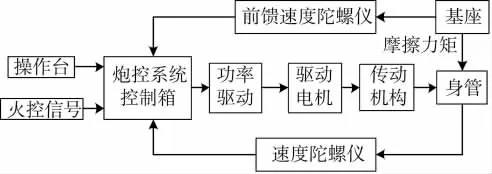
图1 全电式坦克炮高低向伺服系统结构图

1.2 坦克炮控系统的数学模型

本文研究的坦克炮高低向系统是采用交流伺服驱动系统，被控装置主要包括交流电机、减速装置和身管。该系统可以简化为一个二阶系统，控制器将位置误差换算成一个对应于电机理想转速的电压值，然后传递给放大器。其系统框图如图2所示。

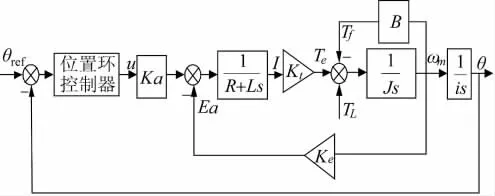
图2 坦克炮控交流伺服系统结构框图

图中：θref为参考位置输入（角度）；θ为坦克炮管高低角；u为控制电压；Ka为放大器增益（含功率放大器）；Ea为电机电枢反电动势；R为电枢回路电阻；L为电枢回路电感；Kt为执行电机力矩系数；Te为执行电机电磁转矩；Tf为摩擦力矩扰动；TL为负载扰动力矩（炮管非平衡力矩）；J为电机转子上的总转动惯量；B为粘性摩擦系数；wm为电机角速度；i为减速比；Ke为执行电机的反电动势系数。

由系统框图可知，执行电机电磁转矩为：

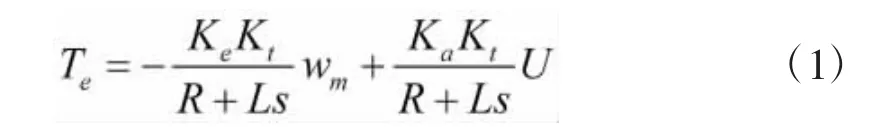
根据系统框图，以及转矩平衡方程可得：

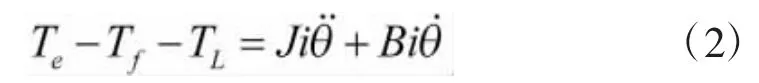
将式（1）带入式（2）得：

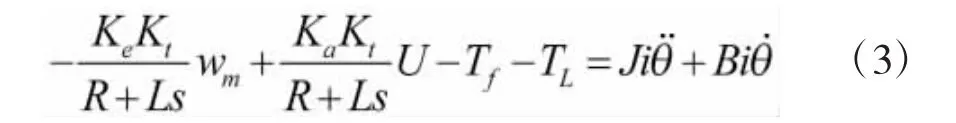
式

（3）两边同乘以1/i，并整理得：

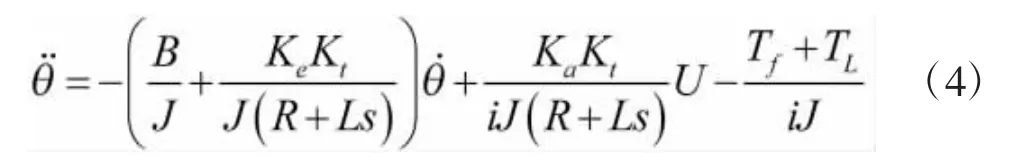
在执行电机工作过程中，其机械时间常数远大于时间常数，因此，可以不计电流响应的延迟时间，即：

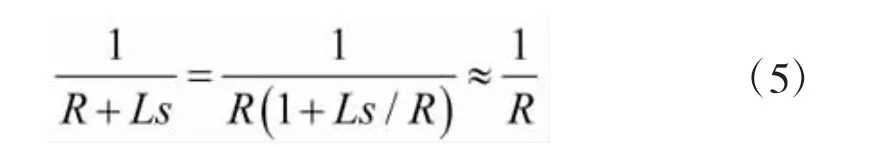
式（4）进一步化简为：

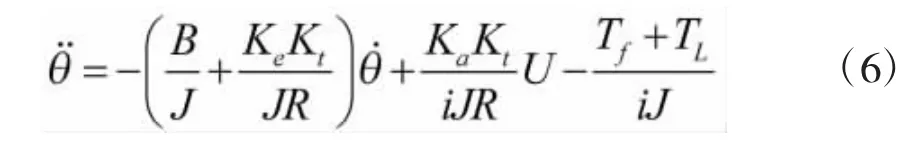
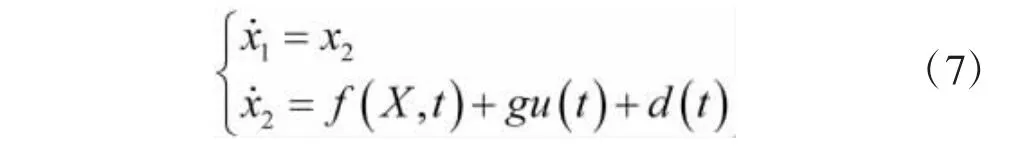
如果不考虑系统误差和测量误差等因素，可以认为f（X，t）、g为确定的，即式（7）为系统的状态方程。但是在实际工作中，由于减速器齿轮组存在间隙，炮管与耳轴之间的摩擦，以及坦克在行进间的外界扰动，导致系统的负载扰动力矩TL、转动惯量J、粘性摩擦系数B、以及摩擦扰动力矩Tf等各参量具有明显的不确定性，且由于工况的变化，系统的状态会产生漂移，因此，系统具有非线性时变动态特征。即在实际工况中，f（X，t）、g是时变的，系统状态方程是不确定的。由分析可知，式（7）可以等价为：

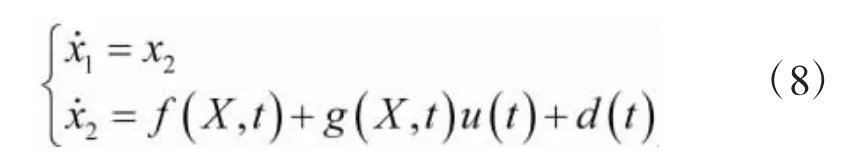
其中，f（X，t）和g（X，t）为未知非线性函数；d（t）为干扰，

2 控制器的设计

2.1 控制律的初步设计

因为f（X，t）和g（X，t）未知，采用RBF神经网络逼近f（X，t）和g（X，t），RBF网络自适应鲁棒滑模闭环控制系统如图3所示：

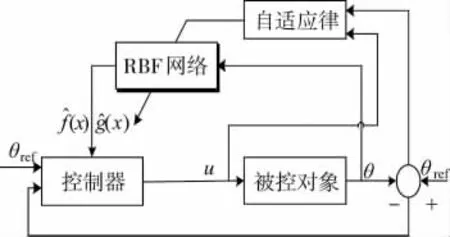
图3 控制系统结构

为了有效消除位置误差并削弱抖动，在滑模函数中加入了位置误差的积分项，位置误差e=θref-θ，则定义滑模函数为

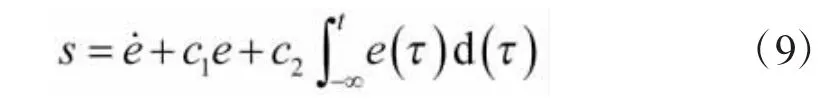
其中，c1＞0，c2＞0，则

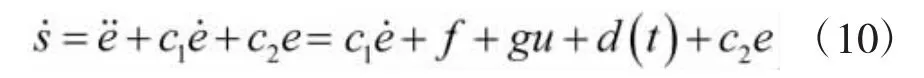
假设f和g为已知，设计控制律为

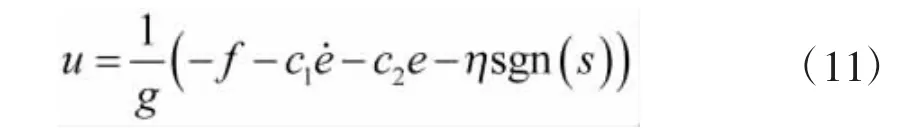
将控制律代入式（10）得

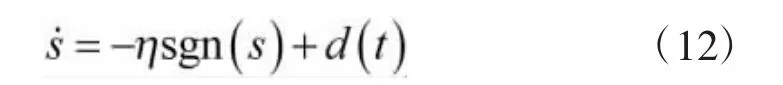
取 η≥C，则

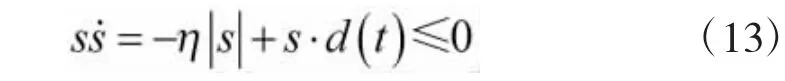
2.2 RBF网络逼近未知函数

采用RBF网络逼近未知函数f（X，t）和g（X，t），RBF网络输入输出算法为［11-12］

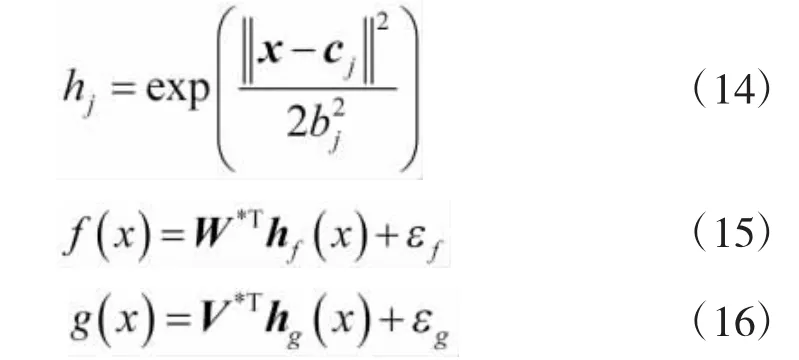
其中，x为网络输入；i表示网络输入层第i个的输入；j为网络隐含层第j个网络输入；为高斯基函数的输出；W*和V*分别为逼近f（x）和g（x）的理想网络权值；εf和εg为网络逼近误差，

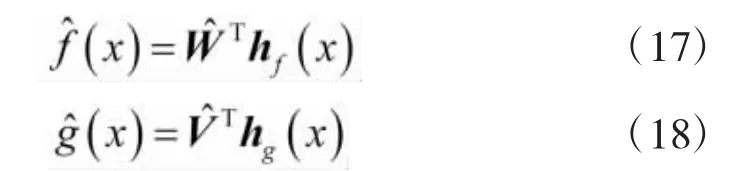
其中，hf（x）和hg（x）为RBF网络的高斯基函数。

经过RBF网络逼近后，式（11）的控制律变为：

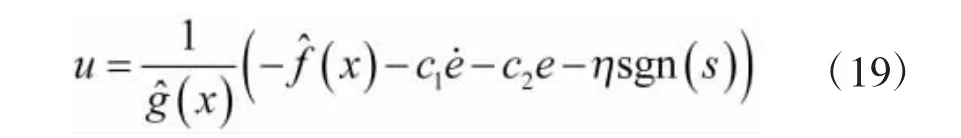
其中，η≥C。

3 稳定性分析

设计Lyapunov函数为：

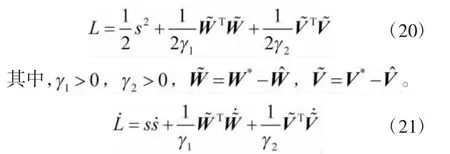
将式（19）代入式（10），并整理得：

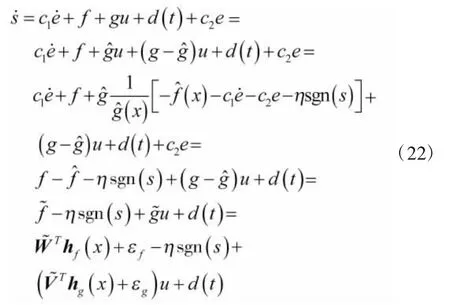
其中，

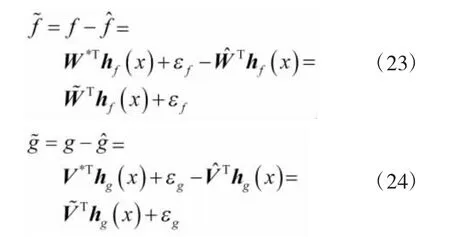
将式（22）代入式（21）得

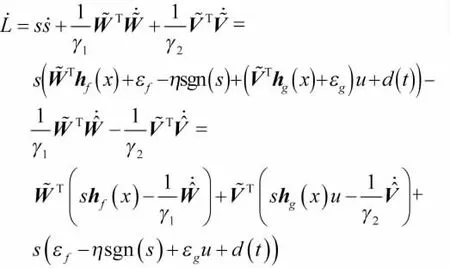
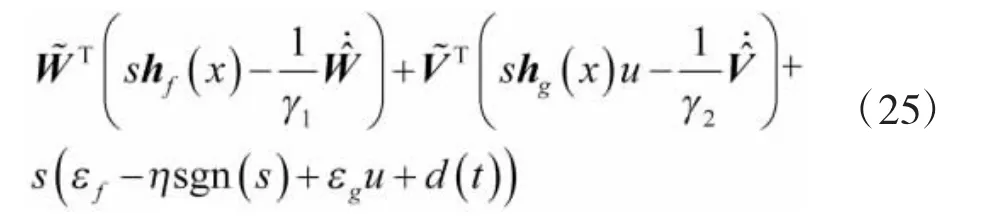
取自适应律为

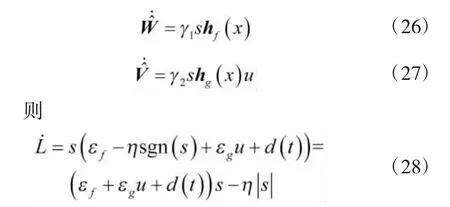
由于RBF网络逼近误差εf和εg为非常小的实数，取，则有。当时，，根据LaSalle不变集原理，时，，这就意味着。可见，控制律中的鲁棒项ηsgn（s）的作用是克服干扰和神经网络逼近误差，以保证系统稳定。

4 仿真分析

本文提出的控制方法的有效性通过数值仿真来验证。仿真中用到的主要参数为：R=0.4 Ω，J=5 239 kg·m2，TL=9.32×103N·m，i=1 039，Kt=0.195 N·m/A，Ke=0.197 V/（rad·s-1），B=1.43×10-4N·m （rad·s-1）。自适应律式（26）和式（27）以及控制律式（19）中的参数取值如下：γ1=10，γ2=1.0，c1=5.0，c2=3.0，η=0.1。RBF 网络结构取2-5-1，cj取［-1.0-0.5 0 0.5 1.0］，bj取5.0，网络权值的初始值为0.10。

为突显本文提出的控制方法的优越性，仿真比较了简单滑模控制和神经网络自适应滑模控制在坦克炮控系统控制效果上的差别。图4是两种控制方法的系统阶跃响应；图5为系统静止时在4 s加入一个480 Nm的阶跃扰动的位置响应曲线；图6为控制器正弦跟踪曲线。

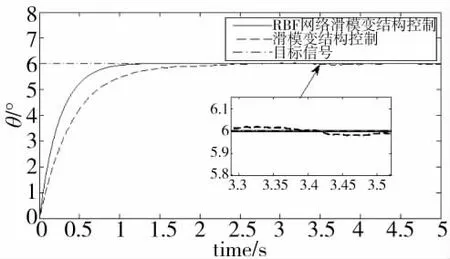
图4 控制系统阶跃响应曲线

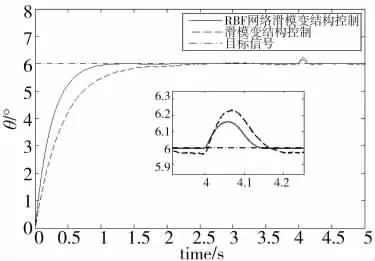
图5 加入负载扰动的阶跃响应曲线

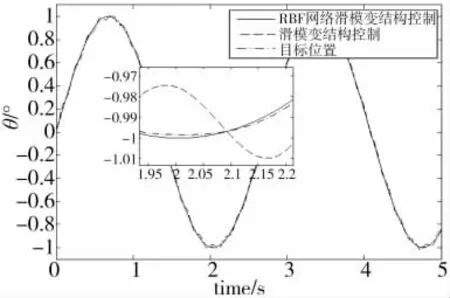
图6 控制器的正弦跟踪曲线

从图4可知，虽然两者都无超调，稳态误差为零，但RBF神经网络滑模控制的响应时间为0.45 s，而基本滑模控制的响应时间为0.8 s。本文提出的RBF神经网络滑模变结构控制响应速度远快于基本滑模控制。同时基本滑模控制有抖振存在，而RBF神经网络滑模控制很大程度上削弱了抖振。从图5可知，当负载出现扰动时，采用RBF神经网络滑模控制，系统产生的偏移较小，且能够更快地恢复到目标位置，因此，本文提出的控制方法抗干扰能力强。从图6可知，由于系统不确定因素的存在，基本滑模控制的跟踪性能变差，且存在抖振现象。本文提出的控制方法跟踪误差小，跟踪性能稳定，且具有良好的瞬态性能。

5 结论

针对坦克高低向炮控系统的非线性时变特征，提出RBF神经网络滑模控制方法。该方法结合了滑模在非线性系统控制中的优越性和RBF神经网络良好的逼近性能，这样既保持了基本滑模控制强鲁棒性的优点，同时滑模本身的抖振很好地被削弱，使系统响应速度快，没有超调和稳态误差，具有良好的动静态性能，能够实现快速平衡跟踪，且系统具有较强的抗干扰能力。仿真结果进一步验证了RBF神经网络滑模控制方法的有效性，能够很好地提高坦克炮控系统的控制性能，具有应用前景。