无刷直流电机的分数阶滑模控制器设计*

刘 宁，赵鸿菲，赵志诚

（1.山西省自动化研究所，太原 030012；2.太原科技大学电子信息工程学院，太原 030024）

0 引言

无刷直流电机由于结构简单，能量密度高，具有优良的调速性能，维护简单方便，工作寿命长，在现代工业领域有着大量的应用［1-2］。在多数应用场合中，传统控制方法能够满足系统的性能要求，但考虑到BLDCM具有时变、多变量耦合等复杂特性，当系统受到外界扰动或系统参数发生变化时，传统控制方法则难以实现对BLDCM的精确控制和满足系统高性能的要求。

滑模控制对系统的参数变化以及外界扰动具有良好的鲁棒性和完全的自适应性，因此，出现了多种BLDCM滑模控制（Sliding model control，SMC）策略［3-7］。然而，在实际应用中，由于时间和空间滞后开关、系统的惯性和延迟及测量误差等因素，使变结构控制在滑动模态下伴随着高频抖振，严重影响了系统的控制性能［8］。为了削弱系统抖振，改进的滑模控制主要包括准滑动模态法［9］、干扰观测器法、滤波法和高阶滑模控制方法［10］等，上述方法在改善系统品质的同时仍然存在着不足，如准滑动模态和干扰观测器会使系统存在静态误差，滤波方法增加了系统稳定性分析的难度，而高阶滑模控制算法的实现较为复杂。

因此，本文结合分数阶控制［11-14］传递能量缓慢，分数阶微积分算子的信息记忆和遗传特性，提出一种分数阶滑模控制策略，分别从滑模面和趋近律两方面进行分数阶滑模控制器的设计。首先对整数阶滑模面的设计进行改进，通过增加分数阶微积分算子，有效削弱滑模控制的抖振作用，又增加了滑模面的自由度。其次采用分数阶型快速幂次趋近律来设计控制律，使系统在加快收敛速度的同时又进一步削弱系统抖振，完成分数阶速度控制器的设计。利用李雅普诺夫理论和分数阶系统稳定性理论进行稳定性分析，仿真结果验证了所提方法的优越性。

1 BLDCM的数学模型

针对两相导通星型三相六状态的BLDCM，在理想状态下，假设电机的反电动势波形为电角度的近似梯形波，不计电机损耗及电枢反应对气隙磁场的影响，三相绕组完全对称，则BLDCM三相绕组的电压平衡方程可以表示为：

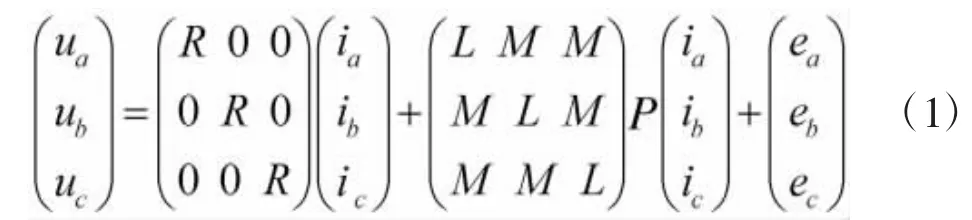
式中，ua、ub和 uc分别为绕组各相电压；ia、ib和 ic分别为绕组各相电流；ea、eb和ec分别为各相反电动势瞬时值；R为绕组相电阻，L、M分别为各相绕组自感和每两相绕组间的互感；P为微分算子。

因三相绕组为星形联结，故ia+ib+ic=0，将此式带入式（1），得到相应的电压平衡方程为：

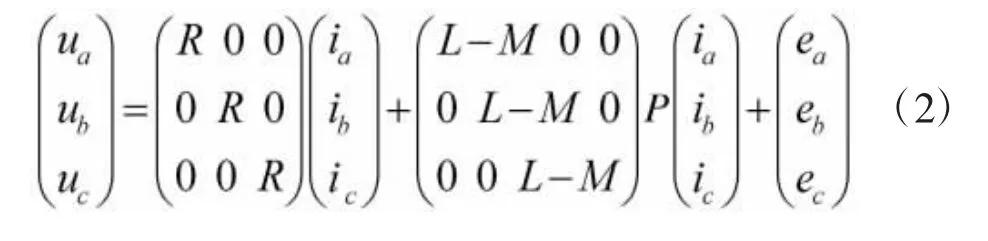
BLDCM电磁转矩方程为：

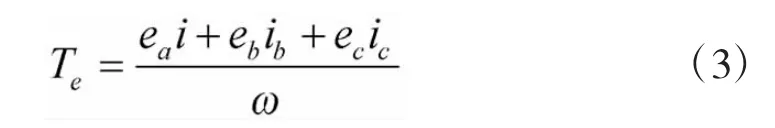
式中，Te为电机电磁转矩；ω为电机转子机械角速度。

BLDCM的运动方程为

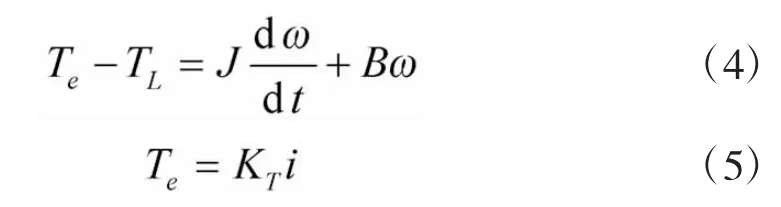
式中，TL为负载转矩；B为粘滞阻尼系数；J为转动惯量，KT为转矩系数。

将式（5）代入式（4）可得

式中，a=B/J，b=KT/J，c=TL/J。

考虑参数变化时，式（6）可表示为

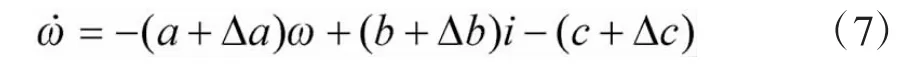
式中，Δa，Δb和Δc为电机参数摄动量。

为了使系统输出的ω快速且平稳地跟踪上设定值ω*，则需要合理地设计控制器，这里定义速度跟踪偏差 e（t）=ω*-ω，根据式（7）可得

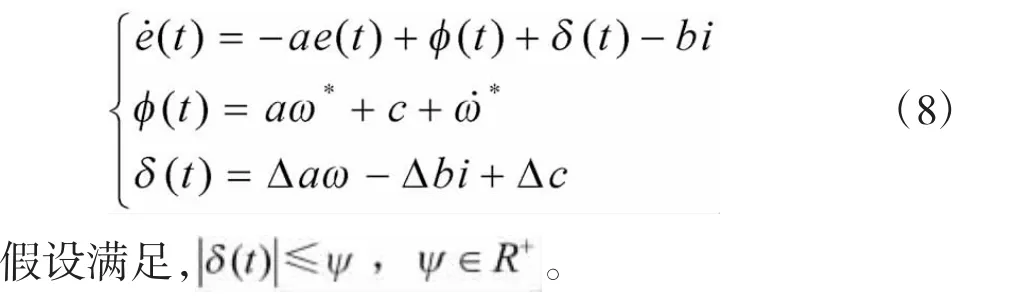
2 BLDCM分数阶滑模控制器设计

2.1 分数阶滑模控制器的设计

分数阶滑模控制器的设计分为两部分，即分数阶滑模面的选取以及控制律的设计。这里选取BLDCM的速度跟踪偏差作为变量，设

利用分数阶微积分随时间缓慢传递能量及衰减的特性来削弱SMC引起的抖振，用分数阶微积分算子代替整数阶微积分算子，通过选择合适的分数阶阶次，增大了控制系统的灵活性。本文选取的分数阶滑模面为

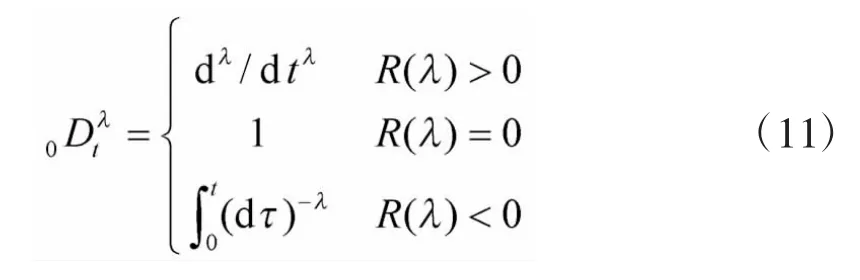
式中，0和t为分数阶计算过程的初始时刻与最终时刻；λ为分数阶微积分阶次；R（）代表λ的实部。

根据式（9）对式（10）进一步计算得

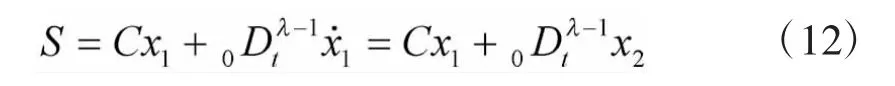
为了使系统的状态尽快地收敛到滑模面上，文献［15］提出了一种快速幂次趋近律，根据文献［16］可知快速幂次趋近律具有二阶滑模特性，结合分数阶传递能量缓慢的特性，对符号函数进行分数阶积分作用，弱化符号函数带来的抖振，设计一种分数阶型快速幂次趋近律，分数阶快速幂次趋近律具体如下：

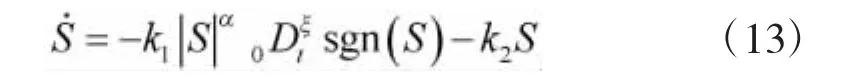
式中，k1＞0，k2＞0，是分数阶微积分算子，其中-1＜ξ＜0，0＜α＜1，sgn（·）为符号函数，其定义如下：

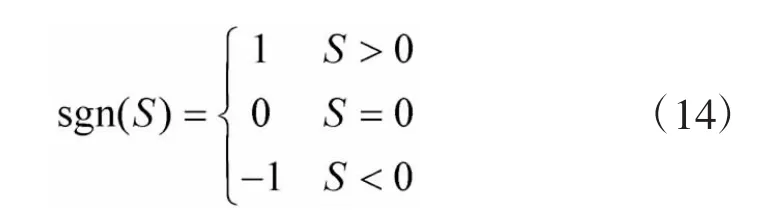
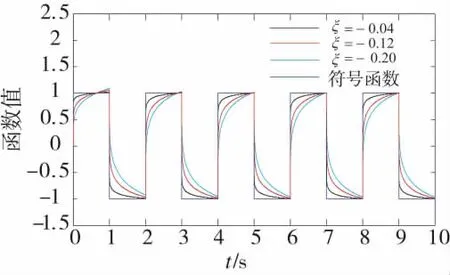
图1 符号函数的分数阶形式

当系统状态远离滑模面时，指数项-k2S起主要作用，加快收敛速度；而在接近滑模面时，项起主要作用。由于对符号函数进行分数阶作用，弱化了由于符号函数带来的不连续作用引起的抖振，且由图1可知，的阶次ξ越高，分数阶对符号函数的作用越强。

由式（12）和式（13）可得

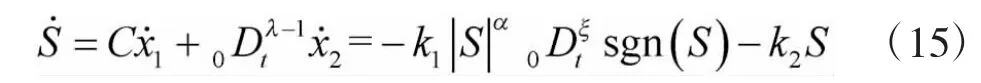
再结合式（8）和式（9）可以设计出分数阶滑模控制器的控制律为

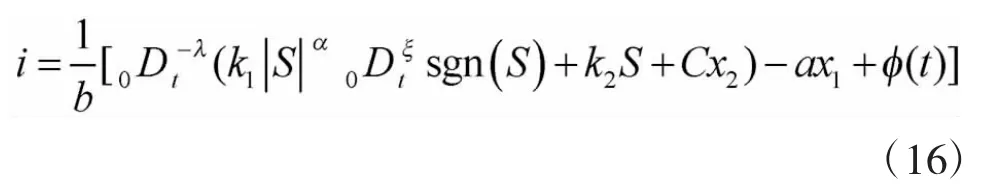
3 控制性能分析

SMC的系统状态包括到达段和滑模段两部分，因此，系统性能的分析也包括两方面内容：一是滑模逼近条件；二是滑模存在条件。

3.1 滑模逼近条件

采用李雅普诺夫定理来证明分数阶滑模控制器的稳定性，定义李雅普诺夫函数为

对式（17）求导，可得

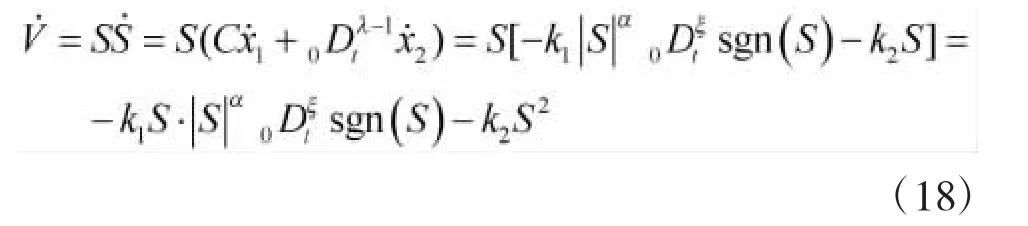
若满足条件 k1＞0，k2＞0，则

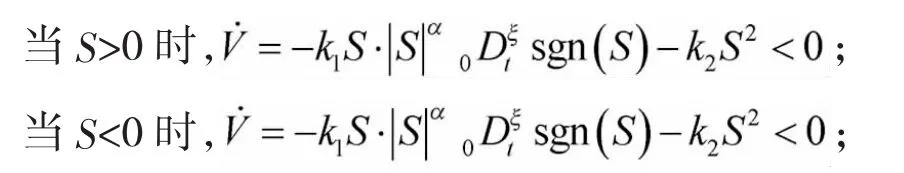
故根据李雅普诺夫稳定性理论，对于任意的S≠0，恒有V˙＜0，系统能由任意初始状态在有限时间内到达滑模面。

3.2 滑模存在条件

当系统进入滑模段时，系统状态满足下列等式：

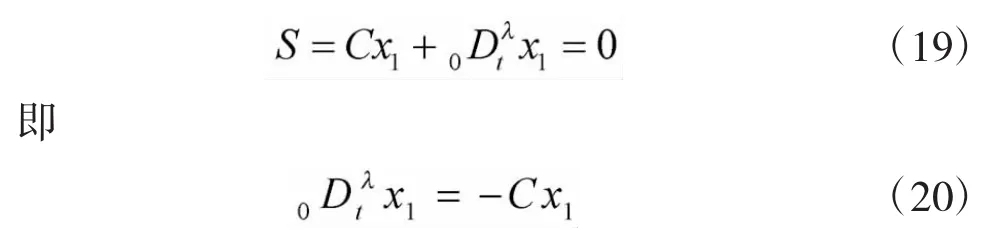
根据分数阶系统稳定性理论［18］，只要满足条件C＞0，则BLDCM分数阶滑模控制系统就是渐近稳定的，且求解式（20）得：

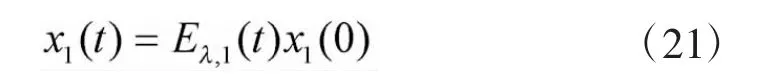
4 仿真结果与分析

为了验证本文所提分数阶滑模控制方法的有效性，将所提控制策略运用到无刷直流电机的调速系统中，利用Matlab软件进行仿真分析，并与传统整数阶滑模控制进行性能比较。无刷直流电机调速系统结构如图2所示，电机的主要参数如表1所示。

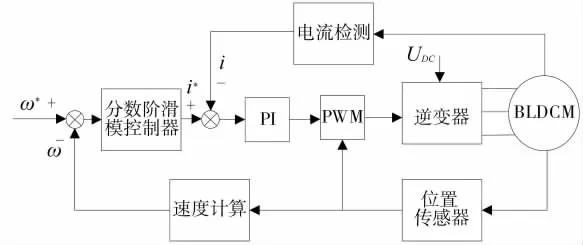
图2 BLDCM分数阶滑模控制调速系统结构图

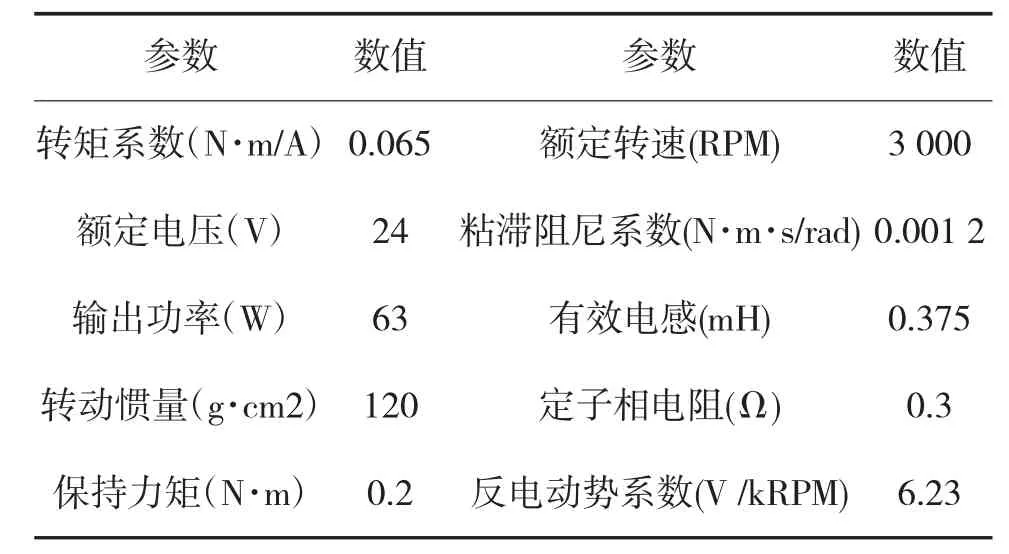
表1 BLDCM参数

首先，进行所提控制策略的抗干扰能力的验证，选用ITAE和超调量σ%作为系统性能，一般情况下，两种性能指标值较小表示性能较好。在给定转速nr=1 000 r/min情况下，在t=0.1 s时，施加负载TL=0.1 N·m，在分数阶滑模控制方法下和整数阶滑模控制方法下的系统转速响应曲线如图3所示，分数阶滑模控制器的分数阶阶次为=0.04，ξ=-0.42，得到的系统性能指标如表2所示。从图3可知，相比于整数阶滑模控制，在分数阶滑模控制下无刷直流电机的转速无超调，对于外部干扰具有较强的抗干扰能力，突加负载后，动态偏差很小，而且分数阶滑模控制可以获得更优异的动态响应速度。

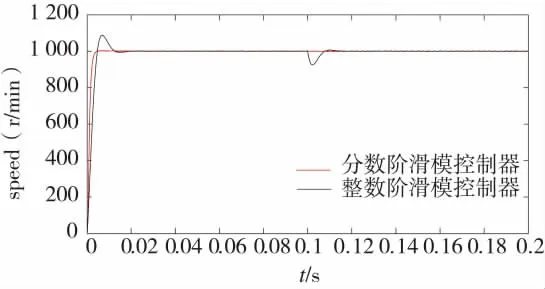
图3 分数阶及整数阶滑模控制的速度响应曲线

为了验证电机参数发生摄动情况下系统的鲁棒性，考虑电机的转动惯量J摄动+30%时，给定转速nr=1 000 r/min，在 t=0.1 s时，施加负载 TL=0.1 N·m，此时得到分数阶滑模控制和整数阶滑模控制的系统转速响应曲线如图4所示，系统的性能指标如表2所示。由图4可知，在电机参数发生摄动后，整数阶滑模控制下的无刷直流电机转速的超调量变大；而同样在电机参数摄动下，对于分数阶滑模控制下的无刷直流电机的转速仍无超调，表2中的性能指标参数同样表明了分数阶控制具有较好的鲁棒性。

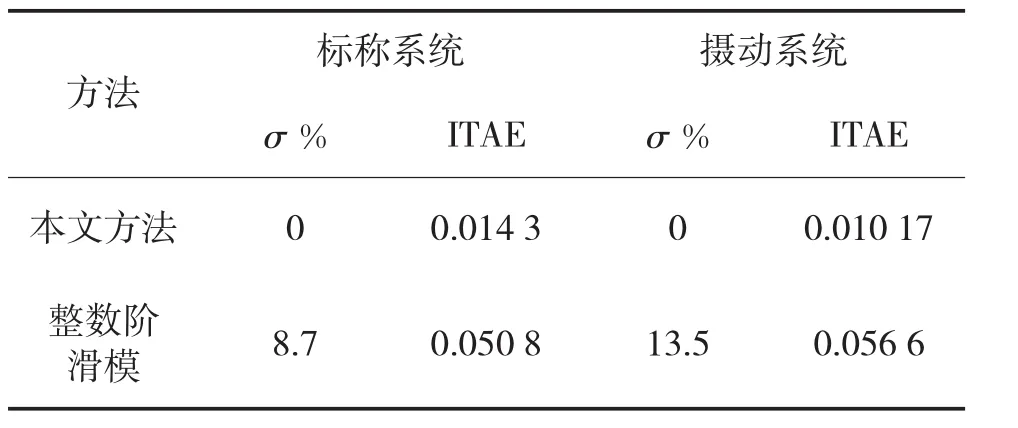
表2 系统性能指标

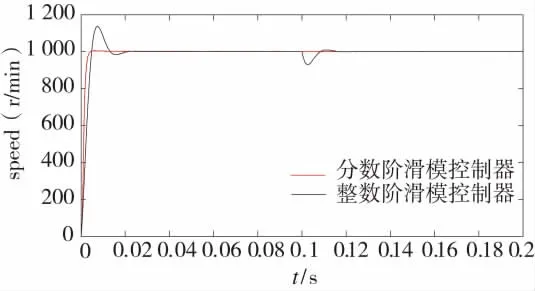
图4 参数摄动下的速度响应曲线

仿真结果验证了与整数阶滑模控制相比，分数阶滑模控制主要特性表现在良好的抗干扰性、强鲁棒性、控制高精度性［20］，可以实现暂态过程中无超调，具有优良的综合控制性能。

5 结论

本文提出了一种无刷直流电机调速系统分数阶滑模控制策略，分别从滑模面和趋近律两方面进行分数阶滑模控制器的设计，削弱了整数阶滑模控制带来系统抖振的同时提高了系统的控制精度。将所设计的分数阶滑模控制器运用到无刷直流电机调速控制系统当中，通过仿真验证了分数阶滑模控制器具有较好的抗负载扰动性能以及对参数摄动具有较强的鲁棒性。