一种新的制导优势模型*

肖冰松，王 瑞，邓有为，王俊迪，向建军

（空军工程大学航空航天工程学院，西安 710038）

0 引言

随着战争形式由平台中心战向网络中心战的转变，网络化条件下的多机编队协同空战的优势和重要性越来越明显，各作战平台相互协作和对武器实行互操作将成为主要作战样式。在网络化条件下，实现多机协同发射与制导空空导弹，成为当前国内外的关注点，相关研究正逐步深入。国外在协同发射与制导方面的公开文献不多，主要集中在海上一体化防空火控体系或导弹、无人机的协同制导律方面［1～7］。国内最近几年正经历着从提出概念到建立模型的过程。文献［8-9］指出了多机空战协同制导的概念。文献［9］对双机编队协同制导的火控机理进行了描述。文献［10-11］对中远程空空导弹多机协同中制导交接方法进行了描述。

现有研究的一个重要方面就是如何选择接替制导的飞机。因为编队内有多架飞机，每架飞机当前所处位置、姿态和自身性能不一样，从而对导弹实施中制导的能力并不完全一样［10］。文献［10］提出了制导优势的概念，用来表征编队内其他飞机对导弹协同制导的能力，并依此选择新的制导飞机。但是文献［10］仅仅是初步提出了概念，涉及的因素很少。后来文献［12］考虑了制导过程中节点受到的目标威胁，构造了武器协调发射和网络制导的优势函数。文献［13-14］构建了我机对目标机制导优先权模型以及我机对空空导弹制导优先权模型。文献［15］从己方飞机对导弹的态势优势、己方飞机对目标的探测能力、己方飞机受到的敌方飞机威胁度和己方飞机空战效能优势函数等4个方面，得到己方飞机对导弹的制导优势模型。这些研究都对制导优势的概念和模型进行了很好的发展。但是这些研究只是对文献［10］的概念从不同角度进行考虑，将距离、角度、速度、高度、雷达性能等独立起来，通过人为加权的方式联立，未确定出这些参数之间的内在联系。特别是未深入研究对导弹制导的主传感器——雷达对目标探测的优势问题。因此，关于制导优势的深化问题还需要持续研究。

歼击机要接替对导弹的制导，其前提必须是歼击机火控雷达已经探测到的目标，稳定获取到目标的距离、角度、速度等信息。因此，本文从机载火控雷达对目标的探测机理出发，从己方飞机火控雷达对目标探测概率的角度，建立一种新的制导优势模型，从而为选择新的制导飞机提供理论支撑。

1 机载火控雷达探测机制

现代歼击机发射中远距空空导弹后，通过火控雷达获取目标的参数对导弹进行制导。因此，目标必须处于火控雷达探测范围内。为了对抗地面杂波，机载火控雷达普遍采用脉冲多普勒（Pulse Doppler，PD）体制。PD雷达为了在中、低空及下视情况下检测出运动目标，需要利用多普勒效应在频域检测出目标信息。但也存在着一些体制上的缺陷，如主瓣杂波盲区和高度杂波盲区［15］，如图1所示。

这样，从不同角度探测目标，PD雷达的探测能力也不一样［16］，例如，等速尾追可能不如侧面飞机探测效果好，如图2所示。

另外，同一个目标，其不同方向的雷达截面积（Radar Cross Section，RCS）也不一样，那么，回波信号功率也不同。因此，雷达从不同方向的探测概率或雷达作用距离也不一样。

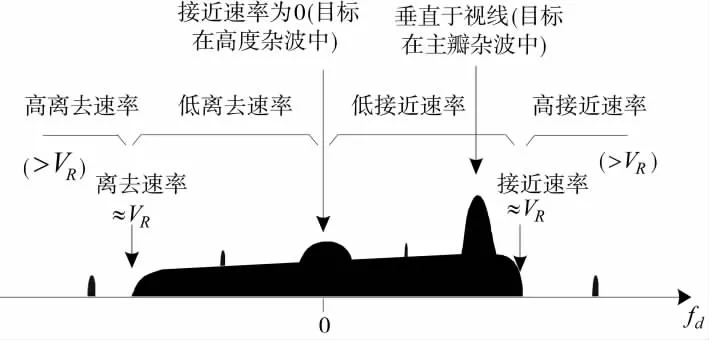
图1 地面杂波频谱与运动目标频谱的关系

所以，对于机载PD火控雷达，载机和目标之间的相对速度会影响探测概率，与角度（包括方位角和进入角）有关。目标的RCS大小也会影响探测概率，也与角度有关。雷达对目标的探测概率大小直接影响目标参数输出的准确性，进而影响对导弹制导的精度和对导弹制导律的要求。

2 制导优势模型

综合上节分析，本节根据载机与目标之间的距离、角度、高度差、相对速度等态势信息，从PD雷达探测盲区入手，计算出目标在不同方向下不同RCS时对应的回波功率，进而计算不同条件下载机火控雷达对目标的探测概率，以探测概率来表征制导优势。

2.1 雷达探测范围

机载火控雷达的探测范围是雷达对目标进行连续观测的空域，取决于最大作用距离Rmax、最大扫描方位角αmax、最大扫描俯仰角βmax。因此，要对导弹进行制导，目标必须处于雷达探测范围内。若目标不处于雷达探测范围内，则制导优势T为0。

2.2 PD雷达探测盲区

空战中，我方歼击机F与目标机T均水平运动，其相对几何态势如下页图3所示。设歼击机运动方向的速度为vR，雷达天线主波束视线与速度视线的夹角为φ，雷达天线视线方向的方位角为α，俯仰角为β。目标的速度为vT，进入角为q。雷达天线视线方向相对目标机的照射方位角为αT，照射俯仰角为βT。歼击机与目标的斜距为R。

其简化的几何态势如图4所示。

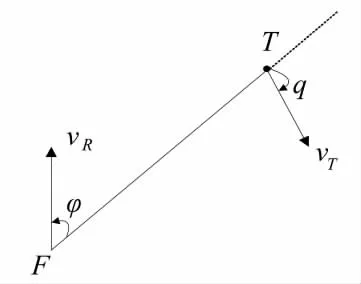
图4 简化的空战态势图

目标视线（FT）：歼击机（F）到目标机（T）的连线；目标方位角（φ）：歼击机航向与目标视线的夹角；目标进入角（q）：目标航向与目标视线延长线的夹角。

文献［16］详细推导了PD雷达的探测盲区模型。

2.2.1 主瓣杂波盲区

若目标与雷达载机的径向相对速度vr处于以下区间时，目标回波频率处于主瓣杂波盲区［16］内。

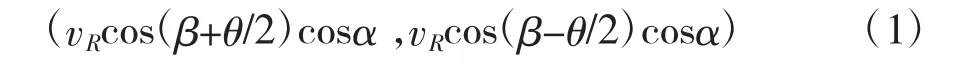
式中，α为扫描方位角，β为天线俯仰角，θ为主瓣波束宽度，vr为目标与雷达载机的径向相对速度，vr=vRcosφ-vTcos q=vRcos α cos β-vTcos αTcos βT，vR为载机运动地速。

2.2.2 高度杂波盲区

若目标与雷达载机的径向相对速度vr处于以下区间时，目标回波频率处于高度杂波盲区［16］内。

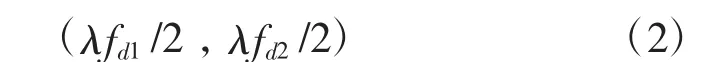
式中，λ 为雷达工作波长，fd1=2vR/λcos（90°+θn/2）cosα，fd1=2vR/λcos（90°-θn/2）cosα，θn为垂直于地面的副瓣的波束宽度。

如果目标处于主瓣杂波盲区或高度杂波盲区，则雷达无法检测到目标，无法制导，所以此时其制导优势T为0。

2.3 不同态势下的RCS

由于飞机的隐身设计，从不同方向照射，其几何截面积、散射系数、方向系数都不一样。因此，飞机的RCS不一样。飞机RCS值的决定十分复杂，只能靠估算的方法取值。本文采用文献［17］中的估算方法。

任何照射角度目标RCS计算公式：

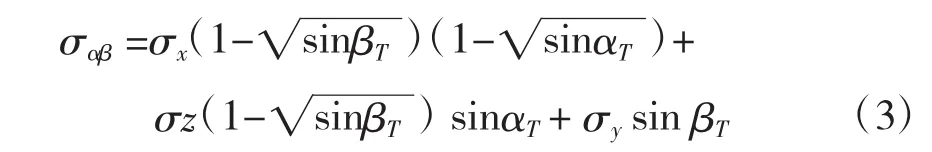
式中，σx为正前（后） 方 RCS，σy为正上（下）方RCS，σz为正侧方 RCS，αT为照射方位角，βT为照射俯仰角。

2.4 不同RCS下的回波信噪比

PD雷达在无杂波区的距离方程［17］为

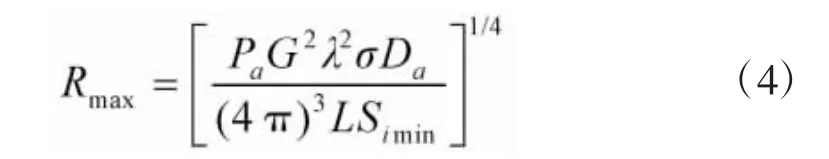
式中，Rmax为雷达最大作用距离，Pa为雷达发射平均功率，G为雷达天线在目标方向上的增益，λ为雷达工作波长，σ为目标平均RCS，Da为PD雷达距离损失系数，L为综合损耗，包括收发综合损耗和大气传输损耗，Simin为最小可检测信号功率。

据此，可得到不同目标距离R和不同雷达截面积σαβ下的回波信号功率

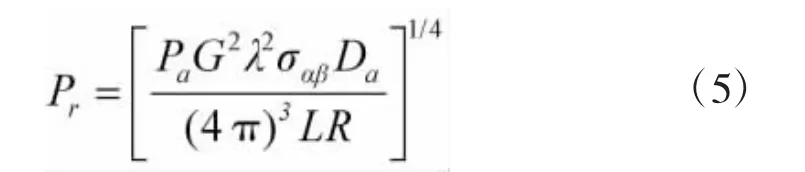
假设雷达在使用中，Pa与 G、λ、Da、L 等参数不变化，即将它们整体视作常数C，则有

将最小可检测信号功率Simin视作雷达接收机的噪声功率，即可得到接收机输出端（针对不同目标距离R和不同雷达截面积σαβ）信噪比SNR：

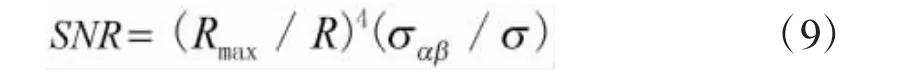
2.5 探测概率

处于运动状态的目标，视角一直在变化，RCS也随之变化。因此，常用Swerling模型来表征其变化情况。不同情况下的目标探测概率也不相同。本文以Swerling I型为例进行说明。

SwerlingI型目标的探测概率PD的精确公式是［18］

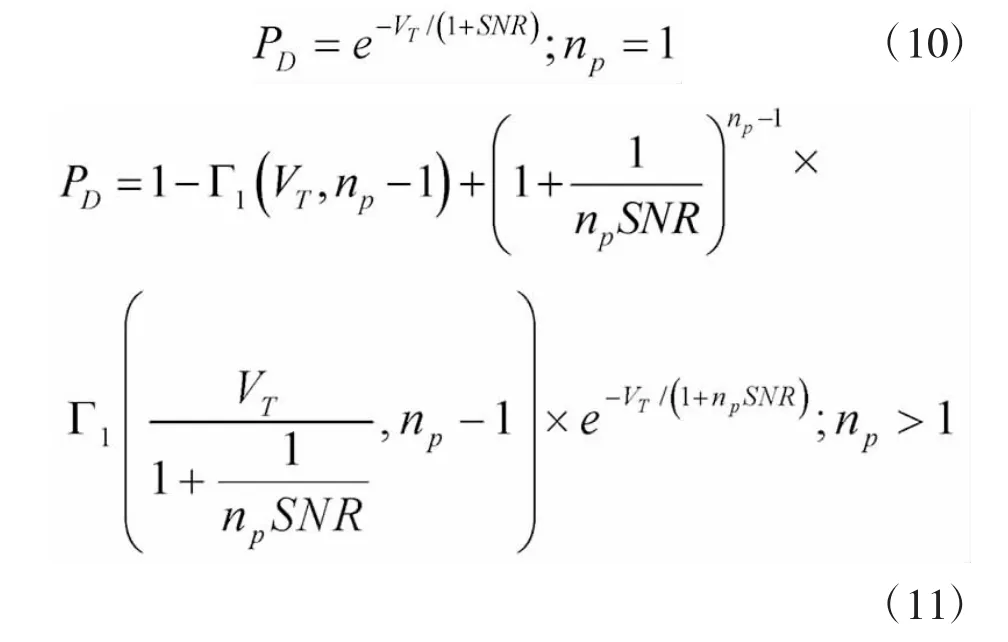
式中，np为积累脉冲数，SNR为信噪比，VT为检测门限，Γ1为不完全γ函数。

2.6 制导优势

综上所述，歼击机对目标机的制导优势T可以探测概率表示为：

制导优势T的计算流程如图5所示。

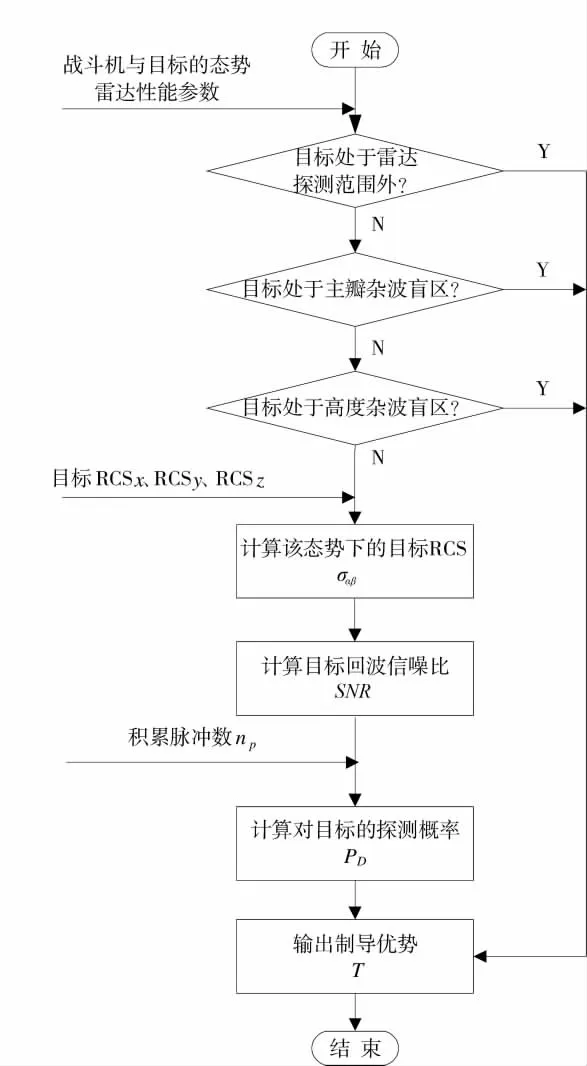
图5 制导优势计算流程

3 实例

假设歼击机配备的雷达参数如下：Rmax=125 km（σ=1 m2），αmax=70°，βmax=70°，θ=3°，θn=20°，np=1，λ=0.03 m。

假设目标飞机的参数如下：σx=0.47m2，σy=115m2，σz=2.6 m2。

假设敌方目标处于我方歼击机探测范围内，且处于杂波盲区外，图6～图9分别反映了不同距离、照射方位角、照射俯仰角下，我方歼击机对敌方目标制导优势的变化趋势。

图6、图7表明，随着距离的增加，制导优势下降，尤其是达到一定距离时，下降迅速。这是因为，目标回波信号强度与距离的4次方成反比，随着距离的增加，目标回波功率会下降，所以对目标的探测概率会下降，从而降低制导优势。而且不同的照射方位角和俯仰角下，目标RCS有一定差别，所以探测概率不同，进而制导优势有差别。

下页图8、图9表明，随着照射方位角或照射俯仰角的增加，制导优势增加。这是因为，目标侧方或上方的RCS通常比平视的正前方要大，所以回波信号强，探测概率高，从而制导优势大。而且，距离越近，回波信号越强，探测概率越高，制导优势越大。

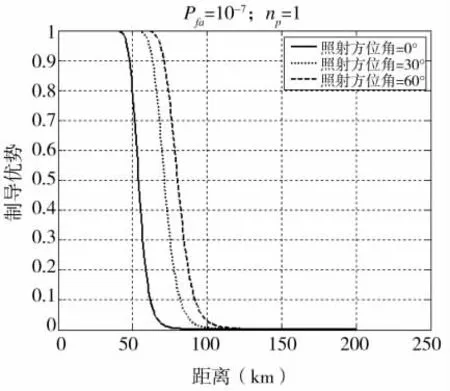
图6 不同照射方位角下制导优势随距离变化情况

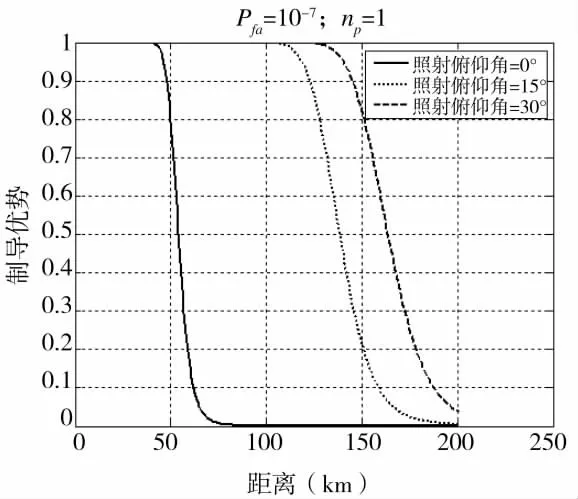
图7 不同照射俯仰角下制导优势随距离变化情况

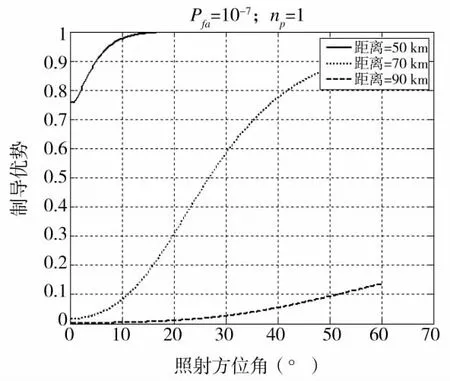
图8 不同距离下制导优势随照射方位角变化情况

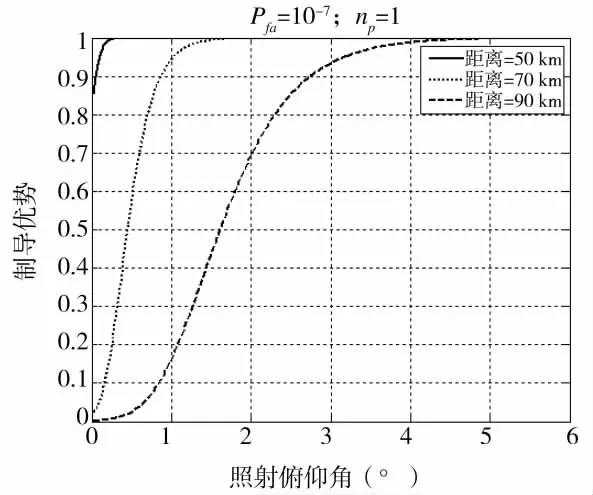
图9 不同距离下制导优势随照射俯仰角变化情况

4 结论

本文根据空战中协同制导的特点，从机载脉冲多普勒火控雷达对目标的探测机理出发，综合考虑目标在不同情况下的雷达截面积对回波的影响，提出了一种新的制导优势模型。实例表明，本文所建立的模型合理、可行，符合不同态势条件下的制导探测要求。该模型不仅可用于计算协同制导的制导优势，亦可用于威胁评估或者态势优势计算中。本文所提方法中仍有不少需要进一步深入研究的地方，尤其是敌方干扰问题还未考虑。下一步将对此模型进一步地完善。