基于外辐射源的AIEKF定位算法*

关 欣，吕政君，许小丰

（1.海军航空大学，山东 烟台 264001；2.通信信息控制和安全技术重点实验室，浙江 嘉兴 314033）

0 引言

外辐射源定位技术具有抗有源定向干扰和反辐射导弹的能力，不仅能够提高战场环境下的生存能力，还可有效发挥侦测、预警等作用，因此，具有非常好的应用前景［1-3］。外辐射源定位系统的观测量主要有方向角、直达波和目标回波的时间差、多普勒频移和方向角变化率，利用不同的测量信息，可得到与测量信息相对应的定位算法。

基于方向角和多普勒频移的外辐射源单站定位系统中，其观测量与目标状态参数具有非线性的函数关系，而EKF是用近似的方法来研究非线性问题的有效方法之一［4］。但由于对非线性模型的线性化处理，所带来的线性化误差会导致预测误差增大，从而对目标状态估计的误差将会逐渐变大，以至于定位结果不理想，甚至出现滤波发散的情况［5］。

为此，对EKF定位算法进行改进，当获得一组观测量时，多次运用EKF滤波公式进行迭代运算，使之不断接近目标实际状态值，当自适应参数达到设定的门限值时，停止迭代运算，此时达到状态估计的最佳，这就是AIEKF定位算法的基本思想。利用此方法，在二维平面内对空中运动目标进行定位跟踪，通过计算机仿真实验，验证了改进算法的定位跟踪性能，并对EKF算法和IEKF算法进行了比较。

1 基本模型

以接收站为坐标原点，建立一个二维观测模型坐标系。单站外辐射源定位模型中接收站、目标和外辐射源之间的位置关系，如图1所示。其中，接收站位置坐标为，运动目标k时刻位置坐标为，速度为，外辐射源位于x轴上，与接收站之间的距离为L。假设接收站可以获得运动目标的方向角θk，也可获得目标与接收站因相对运动而产生的多普勒频移fdk。

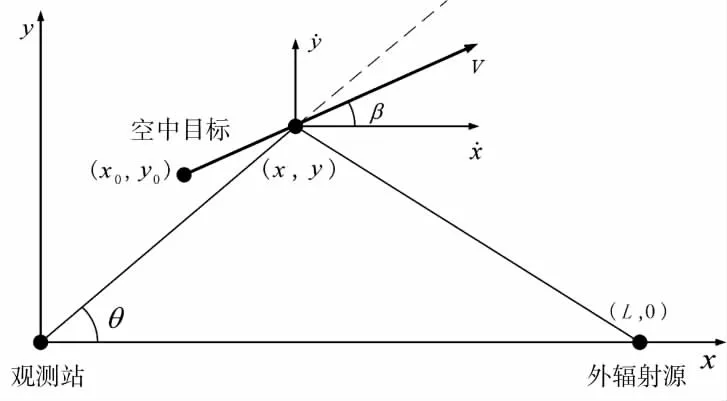
图1 单站外辐射源定位位置关系示意图

首先，接收站获得k时刻目标的方向角θk、多普勒频移则可以建立如式（1），式（2）的观测方程

式中，nθ，nfd分别为方向角和多普勒频移的测量噪声，它们都是统计独立的高斯白噪声，为外辐射源信号波长。

由上面两式可以看出，观测方程均为非线性方程，单站单次测量值无法直接求取目标的状态值，实现即时定位。这就需要积累多次的测量值，通过迭代算法求解目标状态值。

将上述观测方程写成矩阵的形式：

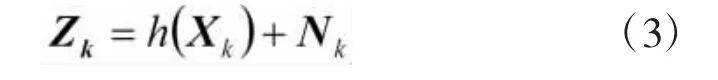
假设空中目标在二维坐标系下作匀速直线运动，系统过程噪声为零，则目标在k时刻的状态方程可以表示为：

2 算法分析

2.1 EKF算法

对于本文研究的定位模型系统，可通过式（3）、式（4）两个方程加以描述。利用EKF算法求解前，首先对观测方程进行线性化，方法是将一阶Taylor展开，并忽略高次项得：

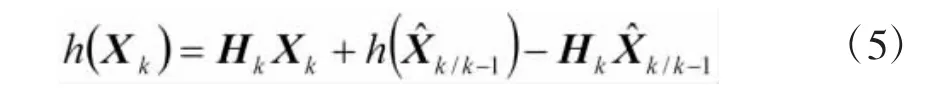
Hk为线性化的Jacobi矩阵，

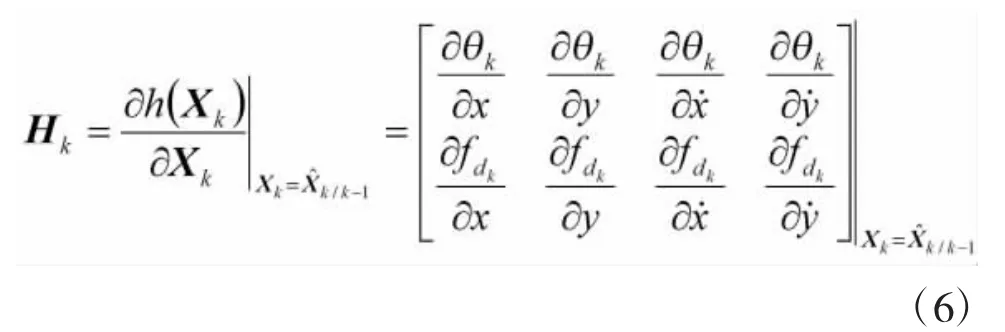
其中：

得到状态转移矩阵A和Jacobi矩阵Hk以后，可以利用EKF算法进行滤波计算，具体递推算法如下：

一步预测：

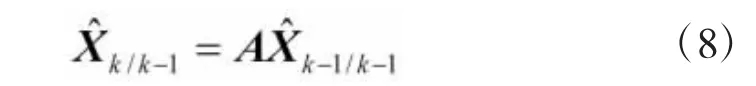
预测误差协方差矩阵：

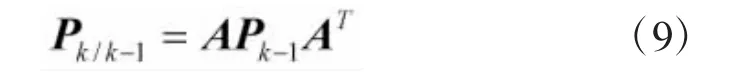
滤波增益矩阵：

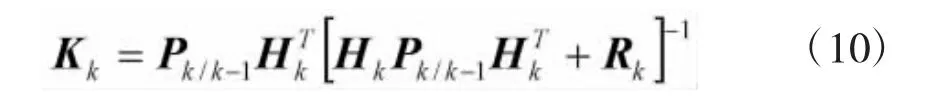
状态更新方程：

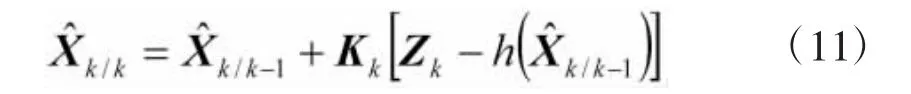
滤波误差协方差矩阵：

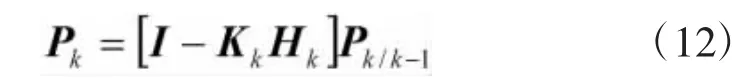
2.2 AIEKF算法

IEKF算法的基本思想是，当获得一组观测量Zk时，多次运用 EKF 公式，使式（10）～ 式（12）迭代循环运算，反复求取状态估计值，使之与观测量逐渐吻合，从而使状态估计最优化。具体算法步骤如下：

1）获得一组观测量 Zk，利用式（8）、式（9）进行一次运算，得到一步预测状态估计和预测协方差矩阵Pk/k-1。

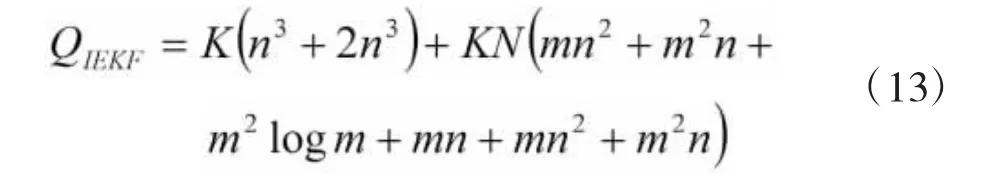
其中，K为观测次数，N为迭代次数，相应的EKF算法的总运算量为：

相比于EKF算法，IEKF算法增加的运算量为：

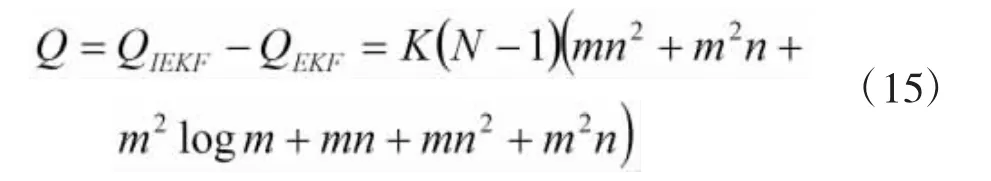
由此可知，在观测次数K一定时，随着迭代次数N的增加，IEKF算法的运算量线性增加，增大了算法复杂度。为此引入参变量α，在每一次观测循环时，自适应控制迭代次数N，当参变量α达到设定门限值α0时，停止迭代运算，进行下一次观测，这就是AIEKF算法的基本思想，算法的流程框图如图2所示。

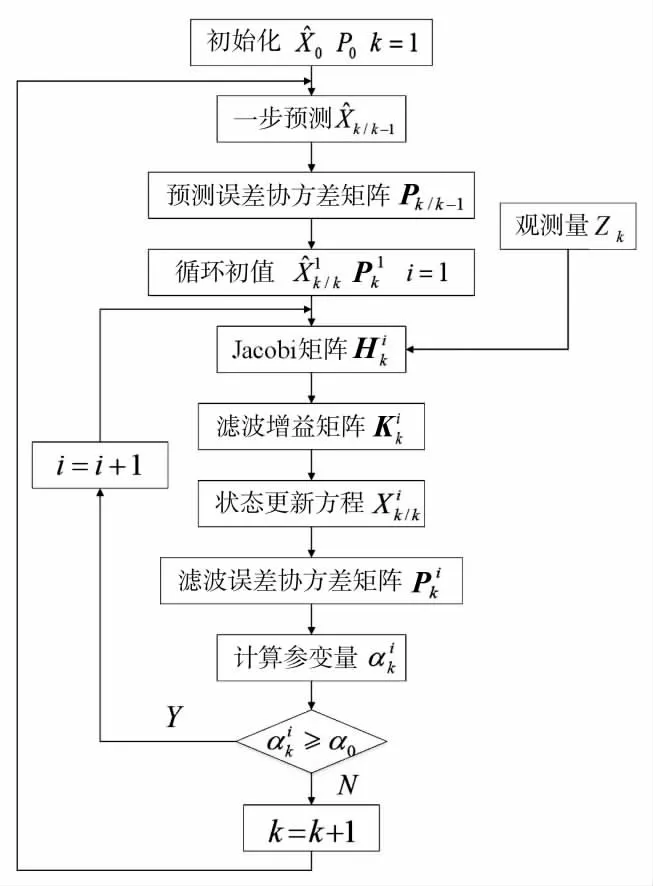
图2 AIEKF算法流程框图

AIEKF算法的每一次迭代运算，都使状态估计值与目标实际状态值渐趋吻合，因此，参变量α应与状态估计偏差正相关。但由于在实际跟踪情况下，目标状态值无法获得，故转为求解状态估计值与观测量之间的相对误差，为此将状态估计值转化为方向角和多普勒频移量，根据式（1）和式（2），推导出式（16）。

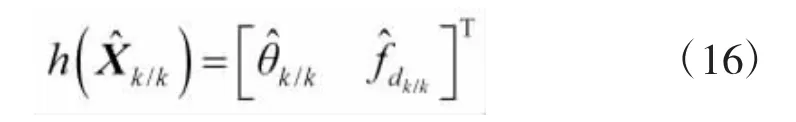
得到参变量α代数式如下：

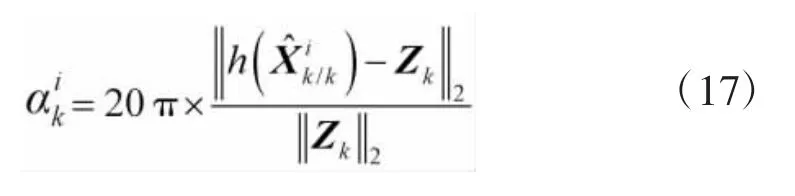
表1 相对定位误差与门限值之间的对应关系

3 仿真实验

为了验证本文AIEKF算法的有效性，本节对该算法进行了仿真试验。试验中，目标跟踪定位模型与第1节所描述的模型相同，地面观测站的坐标为（0，0）km，观测周期T为1 s，观测次数为500次。外辐射源的坐标为（150，0）km，空中目标的初始位置为（100，120）km，空中目标以0.2 km/s的速度远离观测站作匀速直线运动，与X轴的夹角β=30°。方向角的测量噪声是均值为0、方差的高斯白噪声；多普勒频移是均值为0、方差的高斯白噪声。初始协方差矩阵取，参变量门限值取α0=0.25。在上述条件下做500次蒙特卡洛实验，采用均方根误差作为目标跟踪和速度估计的评价指标，定义如下：

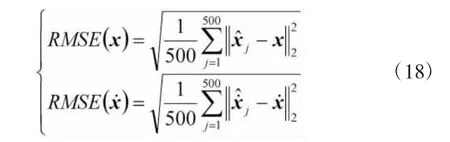
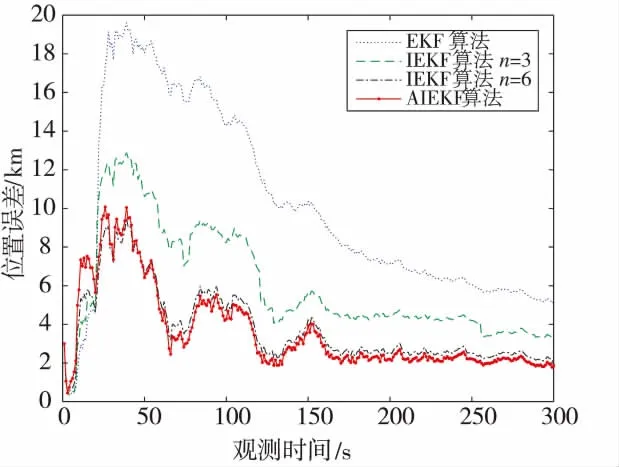
图3 跟踪位置误差曲线

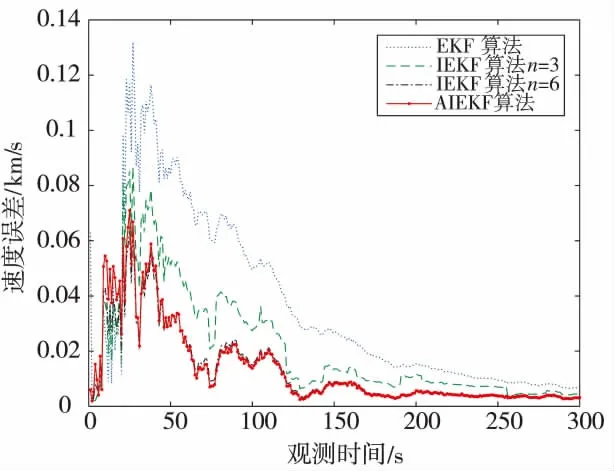
图4 跟踪速度误差曲线

图3、图4分别给出了进行500次蒙特卡洛实验后，对目标位置和速度估计的误差曲线。可以直观地看出AIEKF算法和IEKF算法的跟踪性能明显高于EKF算法，两者都通过多次的迭代运算，改善雅克比矩阵，使估计值与观测值越来越吻合，对于目标的状态估计更准确，收敛速度更快。而AIEKF算法在位置和速度上的跟踪精度与IEKF算法迭代6次的精度几乎相同，且更优于迭代3次的跟踪精度。

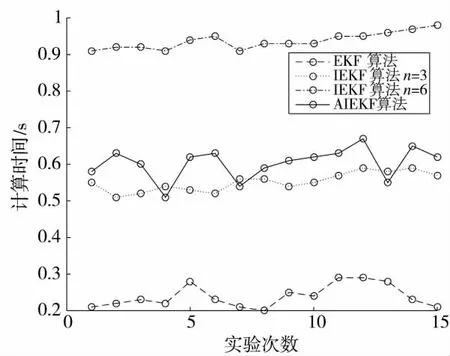
图5 算法运行时间对比图

在2.2节中，已经讨论了IEKF算法和EKF算法的运算量，但由于AIEKF算法在每次观测时的迭代次数都不一样，无法准确统计其运算量。因此，为了更好地比较各算法之间的运算复杂度，对各个算法的运行时间进行了统计，如图5所示。可知EKF算法的运行时间最短，相比于迭代3次的IEKF算法，迭代6次所需时间大幅增加，而AIEKF算法的运行时间与迭代3次的IEKF算法基本相当。

根据以上仿真结果，可以看出AIEKF算法在跟踪精度上远优于EKF算法，在保持相同的跟踪精度的情况下，相比于IEKF算法，AIEKF算法极大地降低运算复杂度。因此，从跟踪性能和运算复杂度两方面综合来看，AIEKF算法要远优于IEKF算法和EKF算法。

4 结论

本文研究了单站外辐射源对空中运动目标的跟踪定位问题，为减小传统EKF滤波算法线性化过程中引入的系统误差，提出了一种通过自适应控制迭代次数求取状态估计值的AIEKF算法。与EKF算法和IEKF算法相比，AIEKF算法既提高了对目标的跟踪精度，又降低了算法的运算复杂度，因此，该算法在目标跟踪定位中有着良好的应用前景。