一种基于加速BP神经网络的PID控制器参数调节方法

徐梦 史豪斌 李继超

摘要：PID控制是一种根据系统的误差，使用比例、积分、微分计算出控制量调节系统误差的控制方法，PID控制器由于不需要建立精确的系统数学模型而广泛应用于工业控制的各个领域。但是经典的PID控制方法的三个参数值通常是人工赋值，而人工赋值往往依赖于经验，因此控制效率较低。B尸神经网络具有很强的泛化能力，可以逼近任意的非线性函数，本文使用BP神经网络调节PID控制器的参数。但是经典BP神经网络需要不断地调节权值，因此收敛速度很慢，本文利用动量常数加速神经网络的训练。仿真试验验证了本文提出的使用加速B尸神经网络调节PID控制器参数的方法具有更快的收敛能力，能够实现系统的快速逼近功能。

关键词：BP神经网络;动量常数;PID控制;仿真试验

中图分类号：TP13 文献标识码：A

PID控制器[1]又称为比例一积分一微分控制器，其结构简单，控制效果良好，是一种在航空航天控制及工业过程控制中常见的反馈回路部件，经典的PID控制器是由比例、积分、微分三个单元的控制器组成。比例控制是PID控制器的基础，积分控制可消除稳态误差，微分控制可加快大惯性系统响应速度以及减弱超调趋势。合理地调节比例、积分、微分控制参数是PID控制器取得良好效果的基础，但是在实际应用中参数的调节往往依赖经验，而经验的获取需要通过大量的尝试，因此，PID控制器参数的整定成为PID性能提高的瓶颈。人工神经网络[2]一直是人工智能领域的研究热点，它从信息处理的角度对人脑神经元网络进行抽象，建立神经元模型，按不同的连接方式构成不同的网络。人工神经网络作为连接主义的典范，它使用广泛互联的结构和有效的学习机制来模仿人类大脑的信息处理过程，不仅是人工智能研究的重要方法，也是当今类脑智能研究的重要工具[3]。BP神经网络是一种按照误差反向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络，因为其具有很强的泛化能力，可以逼近任意的非线性函数，因此，本文使用BP神经网络实现PID控制参数的整定，实现控制参数的自行调节。

PID控制器广泛应用于工业控制领域，也一直是国内外学者的研究热点。

参考文献[4]将PID控制方法应用在四旋翼无人机的飞行控制上，首先对四旋翼无人机进行动力学建模，并在动力学建模的基础上设计了PID控制器，但是经典的PID控制器的增益调节需要耗费大量的时间，因此效率不高。参考文献[5]提出了一种使用BP神经网络的PID控制器参数自整定方法，通过仿真试验验证了所提出方法的效果，但是经典的BP神经网络容易陷人局部最小值，收敛速度较慢。参考文献[6]将Smith补偿控制原理与BP神经网络在线自整定PID控制器结合，可以改善经典BP神经网络（BPNN）的不足，但是在实际生产实践中，这种方法仍然存在收敛速度慢等问题。针对经典BP神经网络收敛速度慢、学习效率不高的问题，本文在BP神经网络反向传播过程中引入动量常数，动量常数使得在垂直向下的方向上具有加速下降的趋势，当学习曲面产生峰和谷时，才减缓这种趋势，使用动量常数可以使得神经网络的训练产生稳定的效果[8]。

1 神经网络加速算法

1.1 BP神经网络

经典BP神经网络是由输入层、隐含层、输出层三部分组成，每一层可以为一层或是多层，BP神经网络中权值的调整采用的是反向传播算法[7]，图1展示了BP神经网络的基本结构。反向传播算法由两部分组成：信息的正向传播与误差的反向传播。在信息的正向传播过程中，输入信息从输入层到隐含层逐层传递直到输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有得到期望的输出，则计算输出层的误差变化值，然后反向传播，通过BP神经网络将误差信号沿原来的连接通路反向传递回来更新各层神经元的权值直至达到期望值。

为提高BP神经网络的训练速度，本文使用一种在反向传播过程中加人动量常数[8]的BP神经网络加速算法。在学习率为常数情况下，使用双曲线正切函数表示S型激活函数，并且在隐含层到输出层之间加人动量常数来加速训练[9]在神经网络的反向传播算法中包含动量常数会对训练产生稳定的效果，通过与经典BP神经网络算法进行分类试验对比，证明了本文提出方法具有更快的收敛速度与学习能力[10，11]。

1.2 BP神经网络加速算法

图1展示了BP神经网络的基本结构，在BP神经网络中，输出层的输入等于隐含层的输出，其余各层中，设某一层中任一神经元j的输入为net_j，输出为y_j，与这一层相邻的低一层的神经元i的输出y_j则计算输出为：式中：a=1.716，b=0.667，θ_j為神经元j的阈值。设定输出层的第k个神经元的实际输出是y_k，输入为net_k，当与输出层相邻的隐含层中第j个神经元的输出为y_j，则y_k和net_k分别为：

BP神经网络的权值通过反向传播的方式进行更新，在权值的第t次迭代过程中，对于一个输入模式x_p^t，若输出层中第k个神经元的期望输出为O_pk^t，实际输出为y_pk^t，则输出层的输出方差为：

若有N个输入样本，则神经网络系统的方差为：

因为连接权值ω_kj^t的修正应该使得方差E_p^t最小，因此ω_kj^t应该沿着E_p^t的梯度方向变化，当输入x_p^t时，ω_kj^t的修正量成正比，可以表示为：式中：k为学习率，0<}刀<1为动量常数，在本文中，动量常数取值为0.95。因此，可以得到：

对于与输出层相邻的隐含层中神经元j和比该隐含层更低的神经元i，权值ω_ji的修正量为：

其中：

因此：

所以可以得到隐含层连接权值的修正量为：

2 加速BP神经网络的PID参数调节模型

图2展示了使用加速BP神经网络调节PID参数的基本结构，加速BP神经网络采用三层结构：输入层、隐含层、输出层。输入层与输出层神经元的个数为3，隐含层神经元的个数为m，使用i表示输入层的神经元节点，使用j表示隐含层的神经元节点，使用p表示输出层的神经元节点。加速BP神经网络的输入层输入的是系统的状态量，即系统在某一时刻的输入量、输出量、输入与输出的差，BP神经网络的输出为PID控制的参数K_p，K_i，K_d。

BP神经网络的输入层输出为：O_i^（1）=x（i），i=1，2，3，隐含层输入为：

隐含层输出为：式中，ω_ji^（2）為输入层到隐含层的权值，f（x）为双曲线正切激活函数，上标（1）、（2）、（3）分别代表输入层、隐含层、输出层，使用双曲线正切函数作为激活函数，神经网络的学习速率会加快，激活函数为：式中，a与b都是常数，两者的取值为a=1.716，b=0.667。隐含层的输出作为输出层的输入，输出层的输入为：输出层的三个输出为：

输出层的三个输出为：

输出层输出的是PID控制器的三个参数，可以表示为：

BP神经网络的方向传播过程使用梯度下降的方法更新权值，如1.2节所述，在反向传播过程中引入动量常数，隐含层到输出层的权值更新公式如式（17）所示：式中e（k）= r（k）-y（k）。本文使用u（k），y（k）的相对变化量估计，如式（18）所示：

PID控制器的输出为：

权值更新公式可以表示为：

3 试验分析

3.1 加速BP神经网络调节PID控制器的实现步骤

使用加速BP神经网络调节PID控制器的具体实现步骤如下：

（1）初始化神经网络的输入层节点、隐含层节点，给出各个层的权值初始值、初始化学习率、迭代次数等。

（2）通过实时采样得到rin（k），y（k），并计算两者的误差error（k）=rin（k）-y（k）。

（3）计算加速BP神经网络的输出，神经网络的输出就是PID控制器的三个增益值。

（4）神经网络通过反向传播算法更新权值，神经网络不同的输出使得PID控制器参数不断调整。

（5）如果达到迭代次数则停止迭代。

3.2 加速B户神经网络调节PID参数对比试验

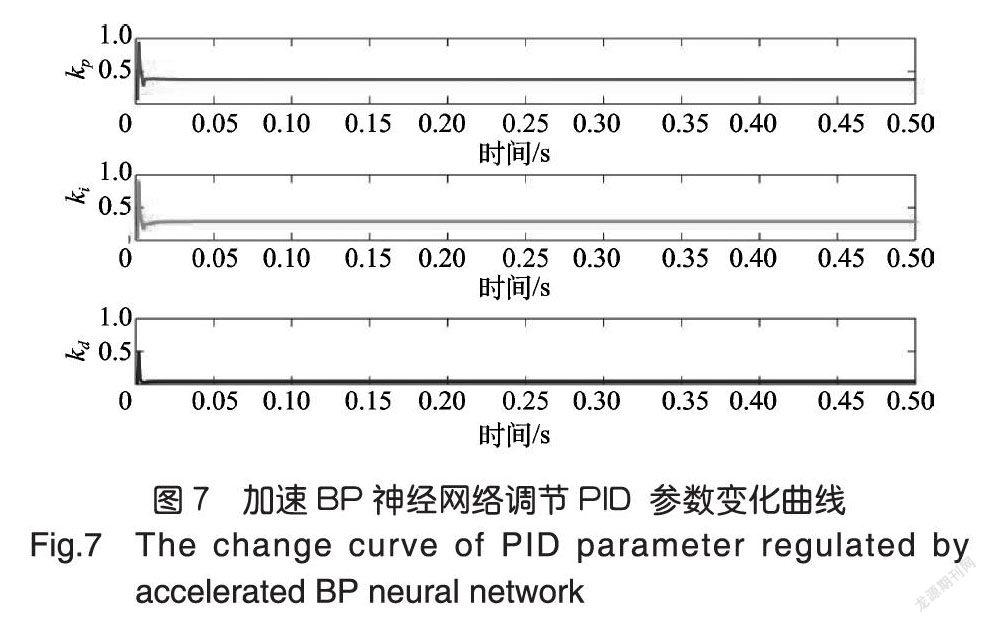
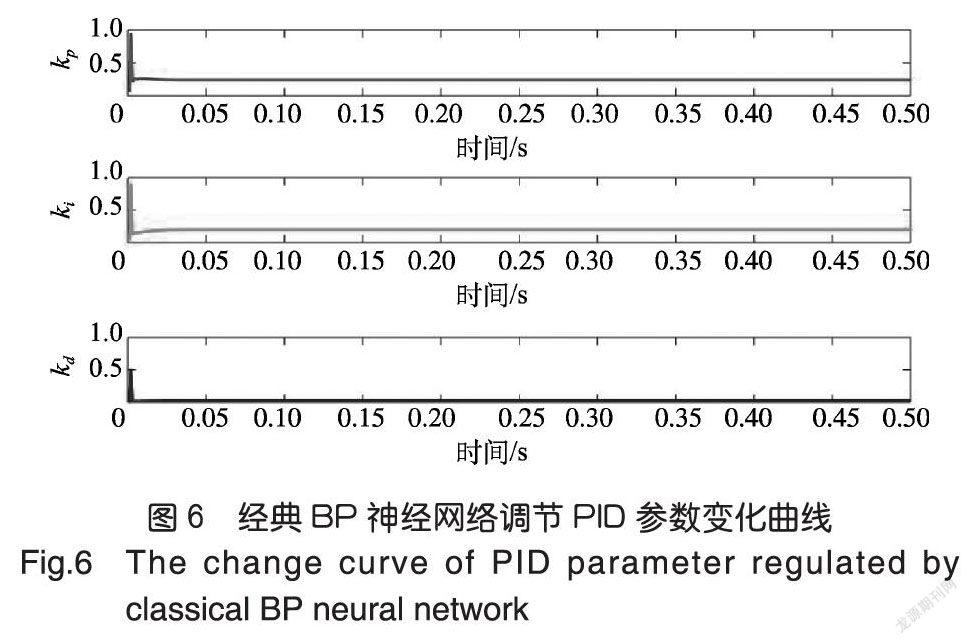
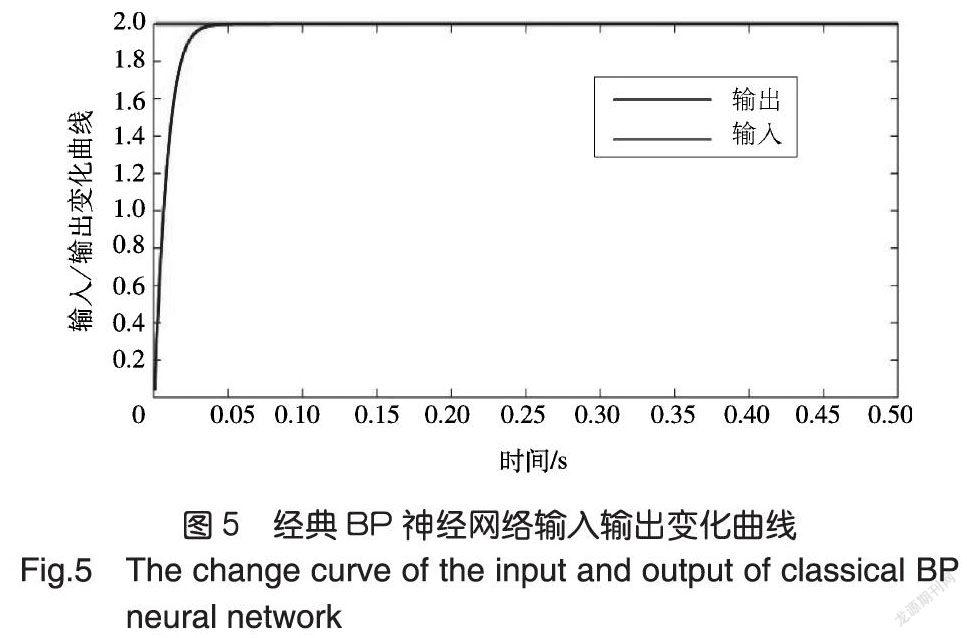
试验对比了加速BP神经网络与经典BP神经网络调节PID控制参数的效果，首先设置试验参数，设置神经网络的学习率为0.3，动量常数为0.25，神经网络的输入层神经元个数为4，隐含层神经元的个数为5，输出层神经元个数为3。图3～图8分别为使用经典BP神经网络与加速BP神经网络（JBPNN）进行系统逼近的试验结果，系统的输入为：rin（x）=1，系统的输出为：

图6～图8分别为使用经典BP神经网络与加速BP神经网络调节PID控制器的输入输出变化曲线与PID控制器的三个参数的输出变化曲线。图5与图8分别展示了使用经典BP神经网络与加速BP神经网络调节PID控制器的输入与输出曲线图，由于PID控制是一种基于误差的闭环反馈控制，当输出等于输入时，完成系统逼近的功能。图3展示了使用经典BP神经网络与加速BP神经网络在学习率为0.3时的误差收敛曲线，误差通过系统的输入与输出做差得到，试验结果表明了使用加速BP神经网络的收敛速度高于经典BP神经网络。为了进一步说明试验效果，本文分别设置学习率从0.05到0.35之间，观察经典 BP神经网络与加速BP神经网络的误差收敛时间随学习率变化曲线，如图4所示，加速BP神经网络的收敛时间总是少于经典BP神经网络，因此，加速BP神经网络收敛效果优于经典BP神经网络。

4 结论

本文对PID控制方法进行了研究，通过分析，可以得出以下结论：

（1）针对经典的PID控制器固定增益、收敛速度慢的问题，设计了一种使用BP神经网络调节控制器增益的智能控制方法，通过训练神经网络可以自适应地调节控制器的增益。

（2）针对经典BP神经网络的不足，使用了一种改进BP神经网络调节PHD控制器参数，该改进BP神经网络在反向传播过程中加人动量常数，并使用双曲正切函数作为激活函数。本文最后设计了使用神经网络调节PID控制器参数的试验，试验结果表明了改进BP神经网络具有比经典BP神经网络更快的收敛速度，能够更快地实现系统逼近的效果，这也验证了本文所提出方法的有效性。

参考文献

[1]Bouabdallah S，Noth A，Siegwart R.PID VS LQ controltechniques applied to an indoor micro quadrotor[C]//IEEE/RSJInternational Conference on Intelligent Robots and Systems，2014.

[2]Afram A，Janabi-Sharifi F，Fung A S，et al.Artificial NeuralNetwork（ANN）based Model Predictive Control（MPC）and optimization of HVAC systems：A state of the art reviewand case study of a residential HVAC system[J].Energy&Buildings，2017，141：96-113.

[3]焦李成，楊淑媛，刘芳，等.神经网络七十年：回顾与展望[J].计算机学报，2016，39（8）：1697-1716.

[4]李俊，李运堂.四旋翼飞行器的动力学建模及PID控制叨.辽宁工程技术大学学报，2012，31（1）：114-117.

[5]廖芳芳，肖建.基于BP神经网络PID参数自整定的研究叨，系统仿真学报，2005，17（7）：1711-1713.

[6]季春光，王朋，李士勇，等.基于神经网络的时变大滞后系统的Smith预估控制[J].哈尔滨工业大学学报，2003，35（3）：303-306.

[7]Khadse C B，Chaudhari M A，Borghate V B.Conjugate gradientback-propagation based artificial neural network for real timepower quality assessment[J].International Journal of ElectricalPower&Energy Systems，2016，82：197-206.

[8]Rumelhart D E，Hinton G E，Williams R J.Learningrepresentations by back-propagating errors[J].Readings inCognitive Science，1986，323（6088）：399-421.

[9]Guyon I，Albrecht P，Cun Y L，et al.Design of a neuralnetwork character recognizer for a touch terminal[J].PatternRecognition，1991，24（2）：105-119.

[10]Watrous R.Learning algorithms for connectionist networks：Applied gradient methods of nonlinear optimization[R].Proc.ICNN-87，1988：619-628.

[11] Jacobs RA.Increased rates of convergence through learning rateadaptation[M].University of Massachusetts，1987.