基于万方和知网数据的期刊量化指标的结构模型建立

温学兵, 王亚静, 刘　洋, 刘瑞银,3

(1. 沈阳师范大学 数学与系统科学学院, 沈阳　110034;2. 沈阳师范大学 学报编辑部, 沈阳　110034; 3. 康涅狄格大学 文理学院, 曼斯菲尔德　06269)

结构方程模型已经广泛应用于心理学、社会学、教育学等领域,在期刊评价领域也逐渐被更多研究学者应用和探讨。2004年,Yue Weiping等首次将结构方程模型应用在期刊评价中,并对各项评价指标分类探讨,但未给出实例研究[1]。2009年,俞立平等采用中国科技期刊引证报告(扩刊版),即万方数据股份有限公司的数据(万方数据),对影响力、期刊特征和时效性3个一级指标10个二级指标建立了测量模型,认为结构方程模型既可以对隐含指标进行评估,还可以对指标进行筛选,并指出基础数据的完备性对评价结果影响巨大[2]。2012年,毛国敏等采用知网的中国学术期刊影响因子年报的量化数据,将5个指标分为影响力因子和传播因子两类,对其进行了相关关系检验,得到了测量模型[3]。2014年,程慧平等采用万方数据将6个期刊量化指标命名为期刊引用因子和期刊来源因子2个一级指标,计算得到了测量模型并分析了一级指标对二级指标解释力强弱的原因[4]。2016年,陈小山等采用知网数据,使用主成分分析方法把13个量化评价指标分类为规模指标、篇均指标、比例指标3个一级指标,再利用结构方程模型方法计算得到了较为理想的测量模型[5]。

由于万方数据的量化评价指标较多且使用了多个较新指标,而在利用国内数据库查阅科研文献时,知网为大多数人采用,故本文采用知网的2个网络下载指标和万方的15个量化指标,利用结构方程模型方法获得了其中12个指标的满足结构方程模型方法所有检测指标要求的测量模型,并得到了结构模型。

1　结构方程模型

Spearman和Wright分别在1904、1918年提出潜在变量的分析模型及更深层次的路径分析[6-7]。在此基础上,瑞典的心理学家、统计学家Karlg Joreskog将回归分析和因素分析结合在一起,开启了结构方程模型的大门[8]。结构方程模型被称为社会科学定量研究领域第3代定量模型和第4代定量模型之间的桥梁,它将测量模型和因果模型二者相结合,实现了社会科学描述性研究和解析性研究的统一。结构方程模型在社会科学领域上的应用越来越多,对问题分析的角度也越来越广泛[9-10]。结构方程模型是由测量模型和结构模型组成,完整的SEM模型应该同时包含测量和结构模型,其原理见文献[11]。

2　初始模型确定及验证

2.1　数据来源

本文采用2016版中国科技期刊引证报告(扩刊版)[12]和中国学术期刊影响因子年报(2016版)[13]中共有的工程技术类307种期刊的量化指标数据。

2.2　指标选择

1) 作为一种验证性方法,结构方程模型方法要求最后每个潜在变量下至少要有3个测量变量;

2) 由于中国科技期刊引证报告(扩刊版)指标多,且总是把新出现的一些量化评价指标纳入报告中,故选择从其2016版的数据中选择使用本方法处理问题的数据;

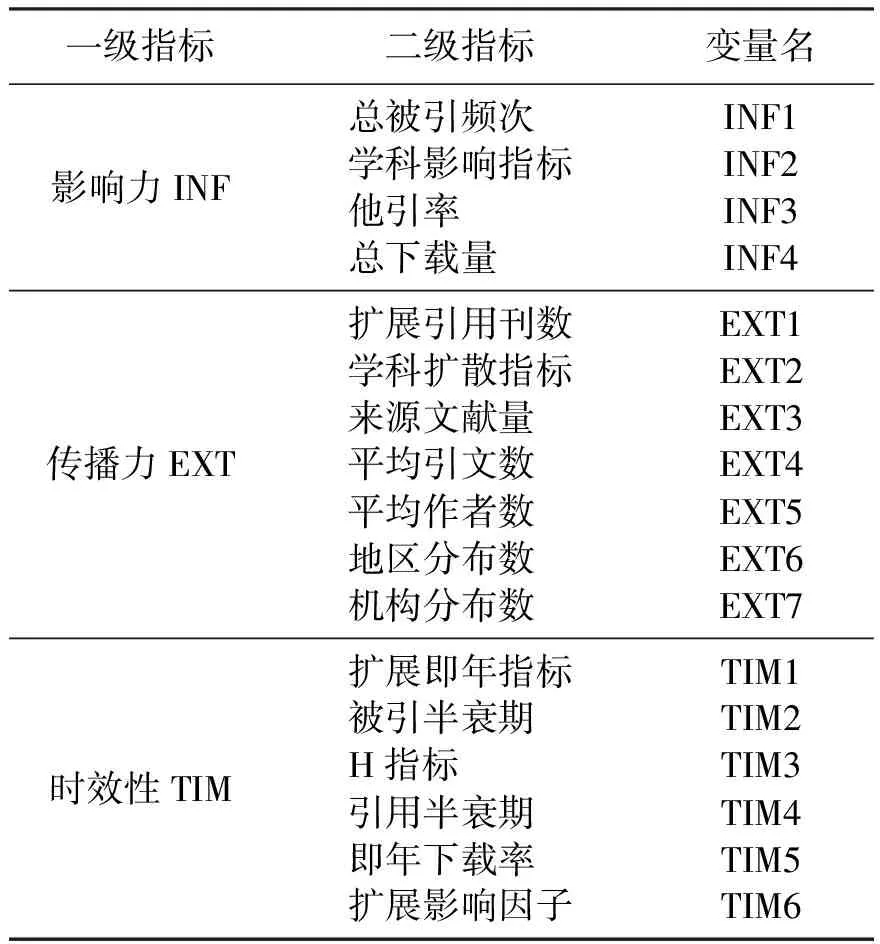
表1　指标及分类Tab.1　Index and classification

3) 研究人员通过网络查阅中文文献时,多数把清华知网作为首选,故选取了知网的2个网络下载指标数据。

2.3　指标归类

本文从指标内涵、区分度、用途和影响等[14]出发,在万方和知网数据中选用了17项评价指标作为二级指标,并把它们归为3类一级指标,即影响力(包含总被引频次、学科影响指标、总下载量、他引率)、传播力(包含扩展引用刊数、学科扩散指标、来源文献量、平均引文数、平均作者数、地区分布数、机构分布数)、时效性(包含扩展即年指标、被引半衰期、H指标、引用半衰期、即年下载率、扩展影响因子)。其中影响力下属的4个二级指标是与期刊总的量化指标有关的,传播力下属的7个二级指标反映了期刊在各个方面的影响程度广度,时效性下属的6个二级指标都是与时间相关的期刊量化指标。指标分类见表1。

2.4　数据预处理

由于数据之间的差异较大,因此将数据进行标准化处理:

标准化处理后的数据均在0～1之间,避免了在不同计量单位下的误差。同时也对数据的效度和信度进行了分析处理,然后运用AMOS 20.0进行统计分析。

2.5　模型假设

初始模型A如图1所示。

图1　初始模型AFig.1　Initial model A

其中:TIM是内生变量;INF是外生变量;EXT是连接内生变量和外生变量之间的中介变量;INF1～INF4是潜在变量INF下设的测量变量;e是测量变量的误差项;是测量变量无法解释潜在变量的部分。同理,EXT1～EXT7、TIM1～TIM6分别是潜在变量EXT和TIM的测量变量。相应的误差项如图1所示。r1和r2分别是潜在变量INF和EXT的误差项。C12表示TIM与EXT之间的相关关系,C13表示TIM与INF之间的相关关系,C23表示EXT与INF之间的相关关系。

通过第一阶段模型的初始检验,结果显示EXT4、EXT5、INF2、TIM4、TIM2并不符合模型理论,因此删去以上测量变量,最终初始模型B为图2。

图2　初始模型BFig.2　Initial model B

2.6　模型识别

模型识别是模型拟合检验的前提,而过度识别要求自由参数个数<待测量数据数,即假定测量变量共有m个,那么待测量数据数DP=m×(m+1)÷2。本例中共有27个自由参数,包括3个已标记的路径系数、9个未标记的路径系数、15个未标记的方差数;共有12个测量变量,即DP=78。由于27<78。因此模型属于过度识别,可以进行下一步验证。

3　模型拟合与修正

AMOS软件共有5种参数估计的方法[15],通常情况下,数据量在300左右要选择最大似然估计;数据量超过1000,选择第5种渐进无母树统计。由于本文数据量为408,选择最大似然估计法。AMOS软件可以处理单一的测量模型,同时也可以处理结构模型。本文应用AMOS 20.0软件进行拟合检验,根据检验结果发现尽管所有指标都满足显著性p<0.05。但是各项适配度指标并不满足优秀拟合结果,如表2所示。

表2　初次模型检验结果Tab.2　Test results of initial model

由于适配度指标并未达到标准,因此要根据修正指标对模型进行修正。修正后适配度指标如表3所示。基本上都满足优秀适配度,说明修正合理。

表3　修正后适配度检验表Tab.3　Revised appropriate checklist

根据标准化结果可以计算出潜在变量的组合信度,组合信度用来表示测量变量与潜在变量之间的结束程度。一般组合信度的检验值为0.5,若组合信度>0.5,则具有良好的组合信度。计算结果如表4。组合信度的计算公式为

其中:Pc为组合信度;λ为因子载荷量;θ为观测变量的残差。

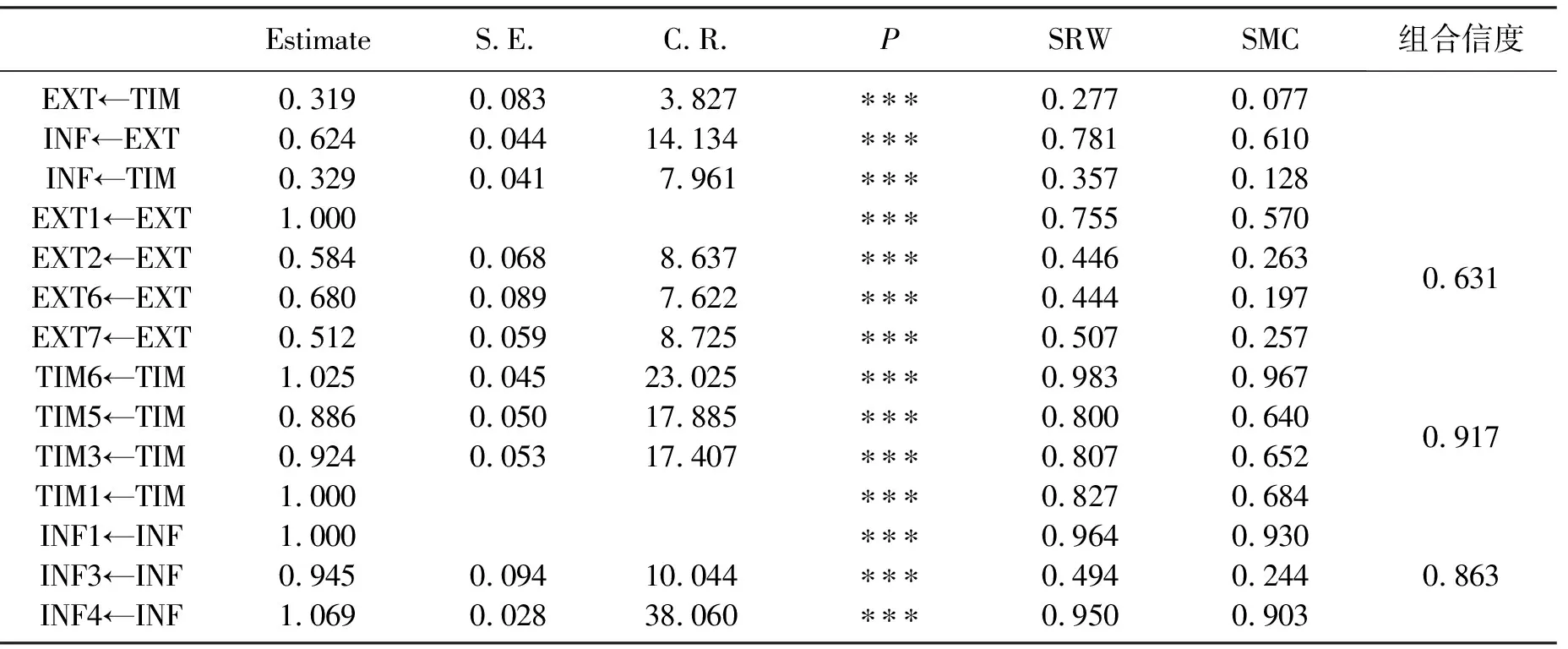
表4　修正模型因子载荷量显著性检验以及组合信度Tab.4　Modified model factor load test and reliability test

4　结　　果

从模型的适配度检验表以及估计值报表可以看出,EXT(传播力)与EXT1(扩展引用刊数)、EXT2(学科扩散指标)、EXT6(地区分布数)、EXT7(机构分布数)之间存在结构关系,且组合信度为0.631;TIM(时效性)与TIM1(扩展即年指标)、TIM3(H指标)、TIM5(即年下载率)、TIM6(扩展影响因子)之间存在结构关系,信度系数为0.917;INF(影响力)与INF1(总被引频次)、INF3(他引率)、INF4(总下载量)之间也存在结构关系,信度系数为0.863。

时效性TIM解释TIM1、TIM3、TIM5、TIM6的能力分别为0.83、0.81、0.8、0.98,表示其解释能力较高,可信度高;而传播力EXT解释EXT1、EXT2、EXT6、EXT7的能力分别为0.75、0.45、0.44、0.51,除EXT1以外其他均属于中度解释能力,这可能与不同学科的学科影响指标之间有不可忽视的差别有关系,而地区分布也会使期刊的传播力受到一定影响。但二者指标均在可以接受的范围;影响力INF解释INF1、INF3、INF4的能力分别为0.96、0.49、0.95,均具有较好的解释能力。

5　结　　语

本文利用知网和万方数据各自的优势,把二者的量化评价指标结合在一起使用,基于结构方程模型方法,利用AMOS 20.0软件,首次获得了满足方法所有指标要求的结构模型,以期为指标的分类研究和评价体系构建提供参考。