一类区间时变时滞切换系统的稳定性
刘玉忠, 佟 雪
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
切换系统是一类动态混杂系统,由一系列连续(离散)时间子系统以及决定子系统间如何切换的规则组成[1]。切换系统作为混杂系统的一个重要分支,在学术界引起广泛关注。随着计算机的发展和普及,为切换系统的兴起、发展和应用提供了物质基础和保障。目前,切换系统的研究已经成为现代控制理论的热点问题,主要集中在系统稳定性分析、系统鲁棒性、系统优化、H∞控制、自适应控制、卡尔曼滤波、系统反馈控制器设计等方面研究中。
时滞现象在自然界中是普遍存在而又不可避免的一种现象,在许多实际系统,如航空航天系统、化工系统、控制系统中频繁出现。一方面,系统时滞可能导致系统不稳定,降低系统性能或者引起系统出现混沌现象;另一方面,也可以利用时滞来改善系统控制效果,更好地解决实际问题。因此,分析和研究时滞动态系统具有极高的理论意义和应用价值。近年来,时变时滞系统的研究引起了国内外众多学者的关注,尤其是对带有区间时滞的线性时变系统的稳定性研究。
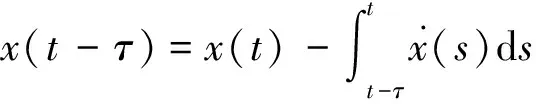
本文研究一类带有区间时变时滞的线性切换系统的稳定性问题。首先,根据时滞分割法将时滞区间进行划分;其次,在每个时滞区间内,通过构造带有三重积分项的L-K泛函,应用积分不等式、二阶倒数凸组合方法,综合处理Lyapunov-Krasovskii泛函沿着时间的导数中积分项;最后,以LMI的形式得出了一类带有区间时变时滞的线性切换系统稳定性的充分条件。
1 问题描述
考虑如下含有区间时变时滞线性切换系统:
(1)
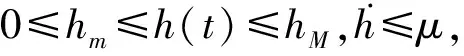
定义1[16]令φ1.φ2,…,φN:RmR在开子集D∈Rm上有正值,则φn在D上的二阶倒数凸组合是以下形式的函数:
(2)

引理1[5]令f1,f2,…,fN:RmR在开子集D∈Rm上有正值,则fi在D上的一阶倒数凸组合满足
(3)
且满足下面的条件:
引理2[17]令h1≤h(t)≤h2,其中:h(t):R+→R+,对于任意R=RT>0,如下不等式成立:
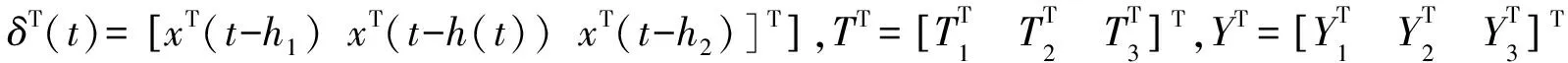
引理3[18]假设γ1≤γ(t)≤γ2,其中γ(·):R+R+,对于任意适当维数的常数矩阵Ξ1,Ξ2和Ω下面的矩阵不等式成立:
Ω+(γ(t)-γ1)Ξ1+(γ2-γ(t))Ξ2<0
当且仅当
Ω+(γ2-γ1)Ξ1<0,Ω+(γ2-γ1)Ξ2<0
引理4[19]假设0≤hm
2 主要结果
考虑如下时变时滞系统:
设N是大于零的正整数,hi(i=1,2,3,…,N+1)为标量,对时滞区间进行如下均匀分割:
hm=h1 定理给定常数hM和hm,如果存在正定对称矩阵P=⎣Pij⎤3×3,Qi>0(i=1,2),Ri>0(i=1,2),Zi>0(i=1,2,3,4),Si(i=1,2,3,4,5),适当的自由权矩阵Ta,Ya(a=1,2,3),使得如下的LMIs成立: 则系统(1)是渐进稳定的,其中 证明为了简单起见,首先考虑h(t)∈[h2,h3]子区间段时,定理成立,进而当h(t)∈[hi,hi+1](i=1,2,3,…,N)时证明定理成立。 当h(t)∈[h2,h3]时,构造如下的L-K泛函: (7) 其中 则V2(t)沿着系统(1)的导数为 (8) 其中 由引理2可得 由引理4可得 由引理4可得 其中α=(h(t)-h2)/h23,β=(h3-h(t))/h23。 由引理1,假设存在矩阵Si(i=1,2,3,4,5)使得式(5)成立,则有 将式(9)~式(17),带入式(8),则 其中 如果对于h(t)∈[h2,h3],有以下条件成立: (18) 注1:本文L-K泛函优越性体现在:基于时滞分割法,将时滞区间划分为均等的n个部分,针对每个区间构造包含三重积分项的泛函,对于L-K泛函中的三重积分增广项,其被积函数中包含状态向量x以及时滞下界的更多信息,这将使得稳定性结论的保守性显著降低。 本文基于时滞分割法,研究区间时变时滞线性切换系统的稳定性问题,不同于以往的研究方法,在构造L-K泛函时,针对不同的分割区间构造包含三重积分项和增广项的L-K泛函,利用保守性更小的积分不等式与二阶倒数凸组合的方法直接处理分段L-K泛函导数中三重积分所产生的积分组合,以便得到其导数的紧致上界。这样的方法避免了以往时滞分割方法判据形式复杂、计算耗时长的不足,有利于理论分析及计算,最后应用线性矩阵不等式得到新的稳定性判据,从而可以利用Matlab求解并验证结论的有效性。

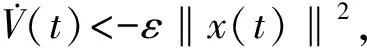
3 结 论

