电动汽车电机滚动轴承故障特征提取方法及仿真分析

苏建芳，吴钦木

（贵州大学电气工程学院，贵州 贵阳 550025）

0　引言

电动汽车具有环保、节能的特点，交通领域欲以此实现该领域节能减排，减少由环境污染和能源短缺所造成的影响。汽车作为人的代步工具，其安全性总是放在第一位。电动汽车的驱动电机是其动力的主要来源，滚动轴承又是驱动电机的核心部件[1]，它的安全性是影响整车可靠性和安全性的关键因素。当电机驱动系统发生故障时，电动汽车的整车性就会受到影响，严重时甚至会导致车毁人亡的事故发生。然而滚动轴承非常容易发生故障现象，更换不及时极易引发交通事故[2]。据统计电机滚动轴承故障发生的概率高达41%。因此，研宄电动汽车电机滚动轴承的故障诊断方法，提高滚动轴承故障诊断的准确性，能够有效地降低交通事故发生的概率，提高其安全水平。

时域或频域分析获取故障信号特征是故障诊断常用的分析方法，比如传统的傅里叶变换可以获取相关的频率特征，其针对于连续平稳信号[3]。但是滚动轴承故障信号是非平稳信号，采用传统的傅里叶变换将会产生严重的频率模糊，这样会导致分析有误差甚至错误[4]。然而小波分析法具有良好的多尺度分解特点和数字显微镜的特性，能提供信号的时域和频域的局部特征，所以非常适合非平稳信号的分析[5]。电动汽车在路面行驶时会产生振动，出现故障时也会出现振动信号，但是根据分析电动汽车行驶时出现的振动频率是很低的，轴承出现故障时振动频率很高，而故障信息都包含在高频部分，所以可以使用振动信号进行分析。本文采用小波分析方法对电动汽车电机轴承进行故障诊断，对采集的滚动轴承故障信号进行分解、重构以及频谱分析，检测出轴承中的故障信息，从而判断轴承发生故障的部位，实现其故障诊断。

1　滚动轴承故障信号系统原理

滚动轴承主要由滚动体、内圈、外圈和保持架组成[6]。机械运转时，可能会因为轴承自身的结构特点、安装不当、润滑不良或者其它物质的腐蚀等造成轴承表面产生损耗和剥离，产生高低不同的凹凸面，转动的滚动体经过这些面时，会造成轴承系统产生激励，导致其产生振动[7]。通过相应的传感器采集轴承振动信号，而采集的振动信号中通常包含了滚动轴承的特征频率信息以及干扰信息。为了得到准确的轴承故障特征频率信息和判断相关故障类型，需要对采集到的振动信号进行合理的处理，这也是本文的一个难点。图1为机械轴承故障信号系统原理示意框图。

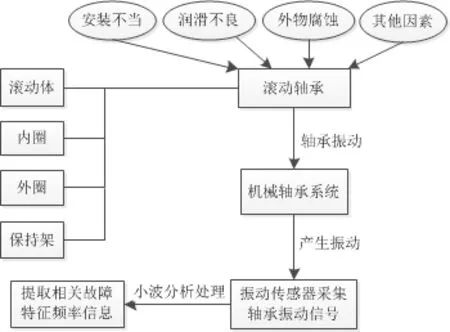
图1　机械轴承故障信号系统原理示意框图Fig. 1 Schematic diagram of mechanical bearing fault signal system

根据轴承元件之间滚动接触的速度关系可以计算其故障特征频率，本文以内圈故障信号为例进行分析，在这里只给出滚动轴承内圈的故障频率计算公式[8]。

D为轴承节径；d为滚珠直径；β为滚珠接触角；n为滚珠个数； fr为转频。用公式(1)可以计算得到的滚动轴承故障特征频率理论值，在试验平台中测量得到的故障特征频率则是此公的整数倍。

2　小波变换理论

小波变换是以信号f(t)与展缩小波函数ψ(t)进行卷积分,将信号分解成位于不同频带和时段内的各种特征信号[9]。小波函数的定义为:设ψ(t)为一平方可积函数,即ψ(t)∈L2(R),若其傅里叶变换ψ(ω)满足以下条件:

则称ψ(t)为一个基本小波或小波母函数。将小波母函数ψ(t)经尺度伸缩和时间平移,便得到一个函数子波簇ψ(a,b)(t)，其形式为：

其中a是伸缩因子；b是平移尺度因子；ψ(a,b)(t)是取决于参数a、b的小波基函数，连续小波变换是将信号f(t)在这个小波基函数下展开得到的，如下:

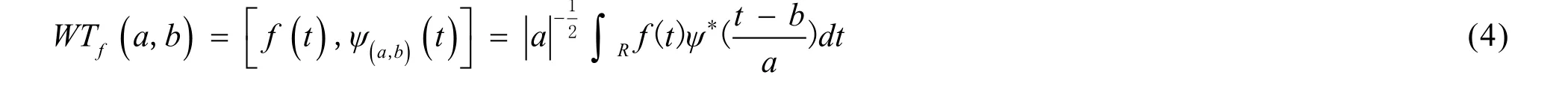
改变a的大小则窗口的形状就会相应改变，即调整子波覆盖的频率范围，实现在频域内的平移；子波时域窗口的位置通过b来调整，即实现小波窗口在时域内的平移；子波能量的归一化是用系数来实现。根据公式(4)，WTf(a,b)变换系数衡量着信号与该子波的相似性[11]。WTf(a,b)越大，说明越相似。所以，需要选择合适的基小波才能很好的提取出信号的特征成分。

在故障特征提取领域，通常选择Daubechies系列小波基，简写为dbN，N表示小波的阶数[12]，此小波扩展性比较好。

3　滚动轴承故障诊断实验及仿真

根据文献[13]中电机轴承的基本信息可知，测试滚动轴承型号为6205-2RS深沟球轴承，接触角β=0°，滚珠个数n=9，轴承节径D=39.04 mm，滚珠直径d=7.94 mm，电机转速是1750 r/min，负载是0，采样频率是12000 Hz。按照第二节中给出的外圈故障频率计算公式可得出内圈故障频率为158 Hz及其倍频。

图2　内圈故障信号时域波形Fig.2 Time domain waveform of inner ring fault signal

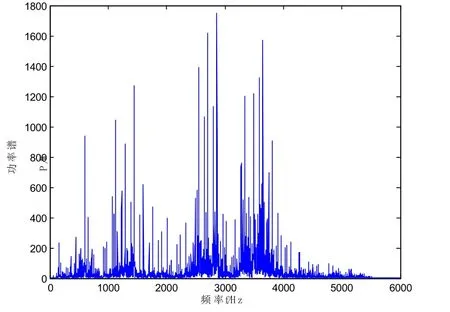
图3　内圈故障信号频谱图Fig.3 Spectrum diagram of inner ring fault signal

本文利用MATLAB对轴承故障仿真信号来验证小波变换分析轴承故障特征是否可行。图2是内圈故障振动信号的时域波形图，从波形图上可以看出没有明显的冲击信号，根本不知道是否存在内圈故障。图3是故障信号频谱图，频谱图中谱线密度较大，振动能量突出，但不易识别出故障特征，需要对信号进一步分析。

已知内圈故障特征频率的理论值为158 Hz。先使用db10正交小波基对滚动轴承内圈的故障信号进行4层小波分解,图4中的d1～d4分别表示了滚动轴承故障信号第1、2、3、4层的细节信号。然后,我们进一步对第1层的细节信号d1做Hilbert变换得到包络波形,再把得到的信号包络做傅里叶频谱分析，结果如图5所示。低频冲击时所产生的高频共振波形包含了丰富的故障特征信息，利用包络分析技术可以对种高频共振波形进行检波和滤波操作，获得放大了的共振解调波，有效地识别出故障类别。因故障冲击波与共振解调波之间存在着对应的关系，因此可以将 Hilbert 分析对滚动轴承故障信号进行解调，得到滚动轴承故障特征的频率值。从图中可以看出,能量在158 Hz处有明显的集中。在158 Hz处出现了尖峰，尖峰值代表了滚动轴承内圈的故障特征频率,正好与计算的理论值相符,从而验证了小波变换在内圈故障诊断中的有效性。

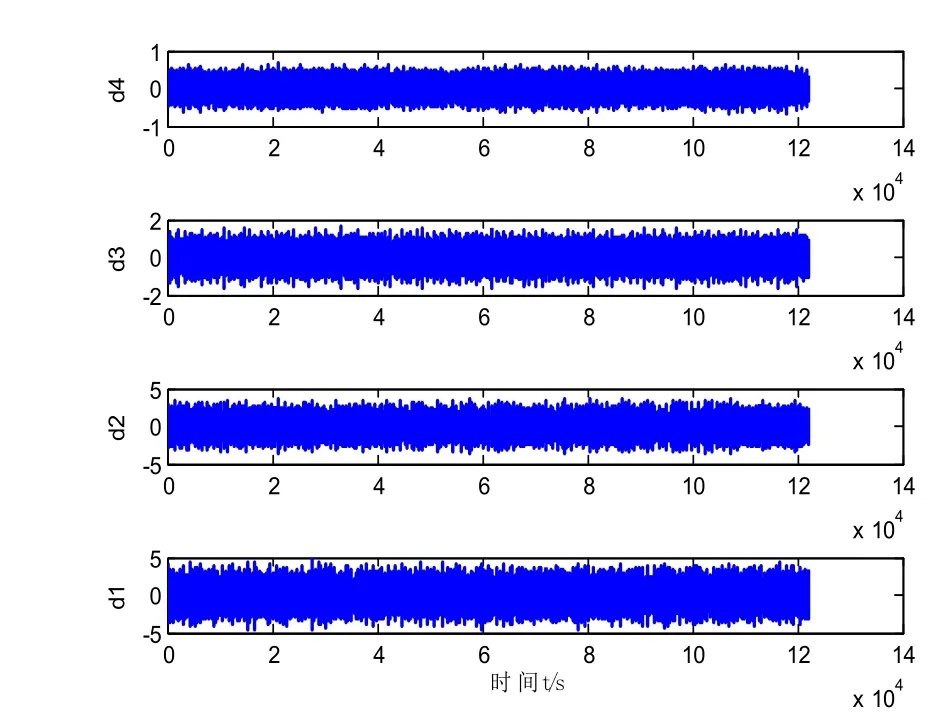
图4　4层db10小波分解结果Fig.4 4 layer db10 wavelet decomposition results

4　结论

图5　第1层细节信号的包络谱Fig.5 Envelope spectrum of first layer detail signal

小波分析对低频信号有很好的频率分辨率,对高频信号有很好的时间分辨率，即具有同时分析信号时域与频域的特性。首先采集电动汽车滚动轴承内圈故障信号，并计算其故障特征频率的理论值，其次利用小波分析对滚动轴承故障信号进行变换，将故障特征进行重构，最后通过Hilbert变换进行解调和细化频谱分析，将其与轴承故障特征频率的理论值相比较,检测出故障发生的部位，从而实现故障诊断。仿真结果证明了该方法的有效性和准确性，为电动汽车在实际的运行环境中快速地进行轴承故障的预知维修提供了一条途径，具有一定的实用价值。